Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 1: Định lí Ta-lét trong tam giác hay, chi tiết giúp học sinh dễ dàng làm bài tập Định lí Ta-lét trong tam giác lớp 8.

Giải bài tập Toán lớp 8 Bài 1: Định lí Ta-lét trong tam giác

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 56 Toán 8 Tập 2: Cho AB = 3cm; CD = 5cm; $\frac{AB}{CD}$  =?

EF = 4dm; MN = 7dm;  $\frac{EF\text{}}{MN}$= ?

Lời giải:

Ta có: $\frac{AB}{CD}=\frac{3}{5};\frac{E\text{}F\text{}}{MN}=\frac{4}{7}$.

Câu hỏi 2 trang 57 Toán 8 Tập 2: Cho bốn đoạn thẳng AB, CD, A'B', C'D' (h.2). So sánh tỉ số $\frac{AB}{CD}$ và $\frac{A\text{}\text{'}B\text{'}}{C\text{'}D\text{'}}$?

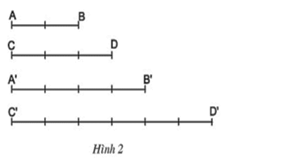
Lời giải:

Ta có: $\frac{AB}{CD}=\frac{2}{3}$

$\frac{A\text{'}B\text{'}}{C\text{'}D\text{'}}=\frac{4}{6}=\frac{2}{3}$

Suy ra: $\frac{AB}{CD}=\frac{A\text{'}B\text{'}}{C\text{'}D\text{'}}$.

Câu hỏi 3 trang 57 Toán 8 Tập 2: Vẽ tam giác ABC trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng a song song với cạnh BC, cắt hai cạnh AB, AC theo thứ tự tại B' và C'.

Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB', B'B và AB, và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC', C'C và AC.

So sánh các tỉ số:

a) $\frac{AB\text{'}}{AB}$ và $\frac{AC\text{'}}{AC}$;

b)  $\frac{AB\text{'}}{B\text{'}B}$và $\frac{AC\text{'}}{C\text{'}C}$;

c) $\frac{B\text{'}B}{AB}$ và $\frac{C\text{'}C}{AC}$.

Lời giải:

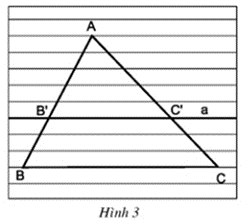
a) Ta có: $\frac{AB\text{'}}{AB}$ = $\frac{AC\text{'}}{AC}=\frac{5}{8}$;

b) $\frac{AB\text{'}}{B\text{'}B}$ = $\frac{AC\text{'}}{C\text{'}C}=\frac{5}{3}$;

c) $\frac{B\text{'}B}{AB}$ = $\frac{C\text{'}C}{AC}=\frac{3}{8}$.

Câu hỏi 4 trang 58 Toán 8 Tập 2: Tính các độ dài x và y trong hình 5.

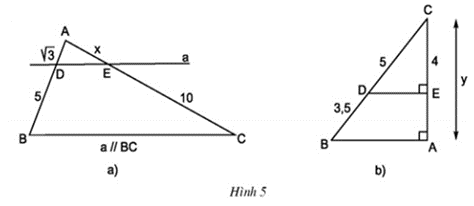
Lời giải:

a)Vì a // BC, theo định lí Ta – lét ta có:

$\frac{AD}{DB}=\frac{AE}{EC}$ thay số $\frac{\sqrt{3}}{5}=\frac{x}{10}$

Suy ra: $x=\frac{10.\sqrt{3}}{5}=2\sqrt{3}$.

b) Vì DE // AB (cùng ⊥ AC), theo định lí Ta – lét ta có:

$\frac{CD}{DB}=\frac{CE}{EA}$

Thay số:

 $$\begin{gathered} \frac{5}{3,5}=\frac{4}{EA} \\ \Rightarrow EA=\frac{4.3,5}{5}=2,8 \end{gathered}$$

⇒ y = 4 + 2,8 = 6,8

Bài tập (trang 58; 59)

Bài 1 trang 58 Toán 8 Tập 2: Viết tỉ số của hai đoạn thẳng có độ dài như sau:

a) AB = 5cm và CD = 15 cm

b) EF = 48cm và GH = 16dm

c) PQ = 1,2m và MN = 24cm

Lời giải:

a)    Ta có: $\frac{AB}{CD}=\frac{5}{15}=\frac{1}{3}$.

b) Đổi 16 dm = 160 cm

$\frac{EF}{GH}=\frac{48}{160}=\frac{3}{10}$;

c) Đổi 1,2m = 120cm.

Ta có: $\frac{PQ}{MN}=\frac{120}{24}=5$.

Bài 2 trang 59 Toán 8 Tập 2: Cho biết  $\frac{AB}{CD}=\frac{3}{4}$ và CD bằng 12cm. Tính độ dài của AB.

Lời giải:

Thay CD = 12cm vào tỉ số độ dài ta được: $\frac{AB}{12}=\frac{3}{4}$

Suy ra: $AB=12.\frac{3}{4}=9$cm

Vậy độ dài AB = 9cm.

Bài 3 trang 59 Toán 8 Tập 2: Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.

Lời giải:

Độ dài AB gấp 5 lần độ dài của CD nên AB = 5CD.

Độ dài A'B' gấp 12 lần độ dài của CD nên A'B' = 12CD.

⇒ Tỉ số của hai đoạn thẳng AB và A'B' là:

$\frac{AB}{A\text{'}B\text{'}}=\frac{5CD}{12CD}=\frac{5}{12}$.

Bài 4 trang 59 Toán 8 Tập 2: Cho biết $\frac{AB\text{'}}{AB}=\frac{AC\text{'}}{AC}$  (h.6). Chứng minh rằng:

a) $\frac{AB\text{'}}{B\text{'}B}=\frac{AC\text{'}}{C\text{'}C}$;

b) $\frac{BB\text{'}}{AB}=\frac{CC\text{'}}{AC}$.

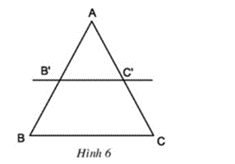
Hướng dẫn: Áp dụng tính chất của tỉ lệ thức.

Lời giải:

a) Ta có: $\frac{AB\text{'}}{AB}=\frac{AC\text{'}}{AC}$

Suy ra: $\frac{AB\text{'}}{AC\text{'}}=\frac{AB}{AC}$ ( tính chất của tỉ lệ thức)

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{AB\text{'}}{AC\text{'}}=\frac{AB}{AC}=\frac{AB-A\text{}B\text{'}}{AC-AC\text{'}}=\frac{BB\text{'}}{CC\text{'}}$  (1).

Vậy $\frac{AB\text{'}}{AC\text{'}}=\frac{BB\text{'}}{CC\text{'}}$

Do đó, $\frac{AB\text{'}}{B\text{'}B}=\frac{AC\text{'}}{C\text{'}C}$.

b) Theo giả thiết ta có: $\frac{AB\text{'}}{AB}=\frac{AC\text{'}}{AC}$

Suy ra: $\frac{AB\text{'}}{AC\text{'}}=\frac{AB}{AC}$  ( tính chất của tỉ lệ thức) ( 1)

Theo a ta có: $\frac{AB\text{'}}{B\text{'}B}=\frac{AC\text{'}}{C\text{'}C}$

Suy ra: $\frac{AB\text{'}}{AC\text{'}}=\frac{B\text{'}B}{C\text{'}C}$  (2)

Từ (1) (2) suy ra:

 $\frac{AB}{AC}=\frac{B\text{'}B}{C\text{'}C}\Rightarrow \frac{C\text{'}C}{AC}=\frac{B\text{'}B}{AB}$

 Vậy $\frac{BB\text{'}}{AB}=\frac{CC\text{'}}{AC}$.

Bài 5 trang 59 Toán 8 Tập 2: Tính x trong các trường hợp sau (h.7):

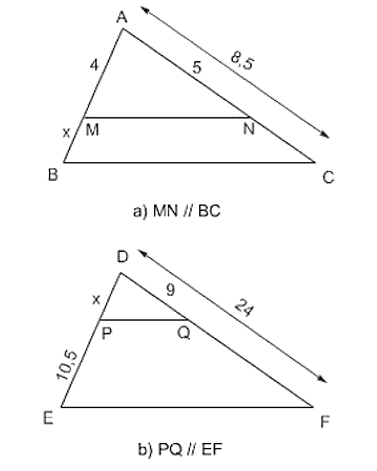
Lời giải:

a) Ta có: MN // BC

Áp dụng định lý Ta - lét ta có:

$\frac{AM}{MB}=\frac{AN}{NC}$

Mà AM = 4, AN = 5, NC = AC – AN = 8,5 – 5 = 3,5

Thay số: $\frac{4}{x}=\frac{5}{3,5}$

⇒ 5x = 4.3,5

⇔ 5x = 14

⇔ x = 14 : 5 = 2,8

Vậy x = 2,8.

b) Ta có PQ // EF

Áp dụng định lý Ta - lét trong tam giác DEF ta có: 

$\frac{DP}{PE}=\frac{DQ}{QF}$

Mà DP = x; PE = 10,5; DQ = 9;

QF = DF – DQ = 24 – 9 = 15

Do đó ta có :

 $\frac{x}{10,5}=\frac{9}{15}$

⇒ 15x = 9.10,5

⇔ 15x = 94,5

⇔ x = 94,5 : 15 = 6,3

Vậy x = 6,3.