Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 3 Bài 1: Định lí Ta- let trong tam giác. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 1: Định lí Ta- let trong tam giác Mời các bạn đón xem:
Bài tập Toán 8 Chương 3 Bài 1: Định lí Ta-lét trong tam giác
A. Bài tập Định lí Ta- let trong tam giác
I. Bài tập trắc nghiệm
Bài 1: Cho AB = 6 cm, AC = 18 cm, tỉ số hai đoạn thẳng AB và AC là?
A.
B.
C. 2
D. 3
Ta có: = =
Chọn đáp án B.
Bài 2: Tìm độ dài x cho hình vẽ sau biết MN//BC
A. x = 2,75
B. x = 5
C. x = 3,75
D. x = 2,25
Ta có: MN//BC ⇒ = ⇔ = ⇒ x = 3.75
Chọn đáp án C.
Bài 3: Cho =
⇔ AB.C'D' = A'B'.CD ( I )
⇔ = ( II )
A. ( I ),( II ) đều sai.
B. ( I ),( II ) đều đúng.
C. Chỉ có ( I ) đúng
D. Chỉ có ( II ) đúng.
Ta có: = ⇒ AB.C'D' = A'B'.CD
⇔ =
Khi đó cả ( I ),( II ) đều đúng.
Chọn đáp án B.
Bài 4: Cho các đoạn thẳng AB = 6cm, CD = 4cm, PQ = 8cm, EF = 10cm, MN = 25mm, RS = 15mm. Hãy chọn phát biểu đúng trong các phát biểu sau?
A. Đoạn AB và PQ tỉ lệ với hai đoạn thẳng EF vs RS.
B. Hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN
C. Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng PQ và EF
D. Cả 3 phát biểu đều sai.
Ta có:
Chọn đáp án B.
Bài 5: Cho các đoạn thẳng AB = 8cm, AC = 6cm, MN = 12cm, PQ = x cm. Tìm x để AB và CD tỉ lệ với MN và PQ?
Ta có:
⇔ ⇔ x = = 9cm
Chọn đáp án B.
Bài 6: Cho tam giác ABC, trên AB lấy điểm M sao cho AM = 4cm và MB = 6cm . Qua M kẻ đường thẳng song song với BC cắt AC tại N biết AC = 20cm . Tính AN?
A. 8cm
B. 10cm
C. 12cm
D. 6cm
M nằm giữa A và B nên: AB = AM + MB = 10cm
Theo định lí Ta let ta có:
Chọn đáp án A
Bài 7: Cho ba điểm A, B và C thẳng hàng sao cho B nằm giữa A và C. Có AB = 7cm và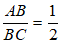 
. Tính AC
A. 14cm
B. 7cm
C. 21cm
D. 28cm
Ta có:
⇒ BC = 2AB = 14cm
Vì B nằm giữa A và C nên: AC = AB + BC= 7 + 14 = 21cm
Chọn đáp án C
Bài 8: Cho tam giác ABC cân tại A có AB = 10cm. Lấy điểm M trên đoạn AB sao cho AM = 4cm, qua M kẻ đường thẳng d song song với BC cắt AC tại N. Tính tỉ số AN và AC?
Vì tam giác ABC cân tại A nên AB = AC = 10cm
Vì MN// BC, theo định lí Ta – let ta có:
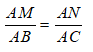
Mà AB = AC nên AM = AN = 4cm
Suy ra :
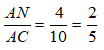
Chọn đáp án C
Bài 9: Cho tam giác ABC vuông tại A có AB = 4cm, AC =3cm. Trên đoạn thẳng AB lấy điểm M sao cho AM = 1cm. Dựng đường thẳng MN vuông góc AB. Tính BN
Áp dụng định lí Py ta go vào tam giác ABC có:
BC2 = AB2 + AC2 = 42 + 32 = 25 nên BC = 5cm
Ta có: nên AC // MN
Áp dụng định lí Ta let ta có:
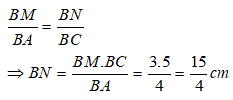
Chọn đáp án A
Bài 10: Cho tam giác ABC, một đường thẳng d song song với BC cắt AB và AC theo thứ tự tại M và N biết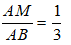 
và AN + AC = 16cm. Tính AN
Ta có: MN // BC , theo định lí ta let ta có:
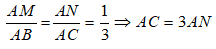
Lại có: AN + AC = 16cm nên AN + 3AN = 16
Suy ra: 4AN = 16 nên AN = 4cm
Chọn đáp án D
II. Bài tập tự luận có giải
Bài 1: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Lời giải
Bài 2 Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Lời giải
Theo định lý Ta-lét:
Vậy cả 4 khẳng định đã cho đều đúng.
Bài 3 Cho hình bên, biết DE // AC, tìm x:
Lời giải
Vì DE // AC, áp dụng định lý Talet, ta có:
Bài 4 Cho hình bên biết ED ⊥ AB, AC ⊥ AB, tìm x:
Lời giải
Ta có: ED ⊥ AB, AC ⊥ AB ⇒ DE // AC (từ vuông góc đến song song), áp dụng định lý Talet, ta có: 
⇔ x2 + 6x – 27 = 0
Vậy x = 3
Đáp án cần chọn là: A
Bài 5 Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
Lời giải
Áp dụng định lý Ta-lét:
Bài 6: Viết tỉ số của hai đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD = 15 cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
Lời giải:
Bài 7
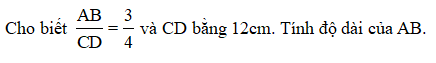
Lời giải:
Thay CD = 12cm vào tỉ số độ dài ta được:
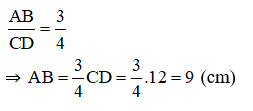
Vậy độ dài AB = 9cm
Bài 8 Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.
Lời giải:
Độ dài AB gấp 5 lần độ dài của CD nên AB = 5CD.
Độ dài A'B' gấp 12 lần độ dài của CD nên A'B' = 12CD.
⇒ Tỉ số của 2 đoạn thẳng AB và A'B' là:
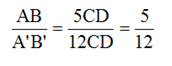
Bài 9
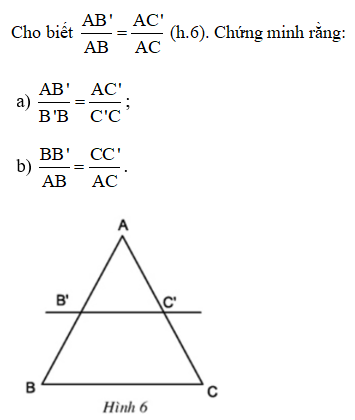
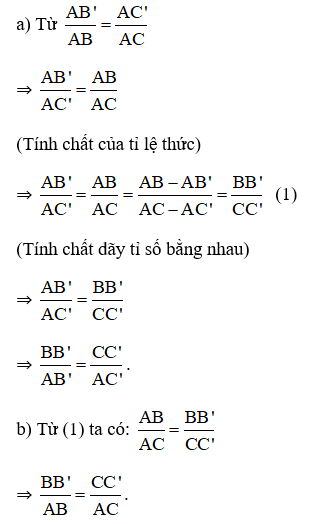
Hướng dẫn: Áp dụng tính chất của tỉ lệ thức.
Lời giải:
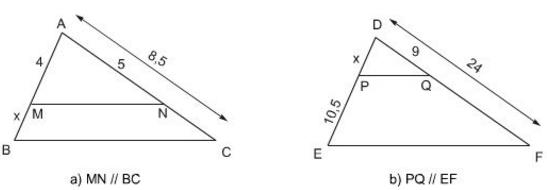
Bài 10 Tính x trong các trường hợp sau (h.7):
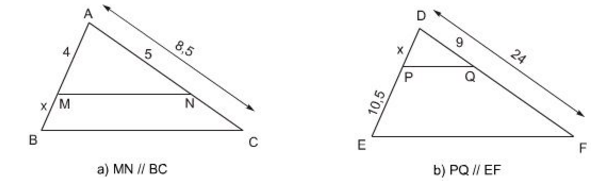
Lời giải:
a) Ta có: MN // BC
Áp dụng định lý Ta-let ta có:
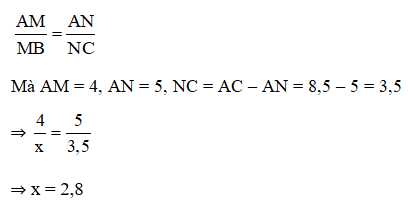
Vậy x = 2,8
b) Ta có PQ // EF
Áp dụng định lý Talet trong tam giác DEF ta có:
Vậy x = 6,3.
III. Bài tập vận dụng
Bài 1 Cho AB = 3cm; CD =5cm;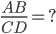 
= ?; EF = 4dm; MN = 7cm;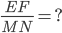 
Bài 2 Cho bốn đoạn thẳng AB, CD, A'B', C'D' (h.2). So sánh tỉ số
Bài 3 Vẽ tam giác ABC trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng a song song với cạnh BC, cắt hai cạnh AB, AC theo thứ tự tại B' và C'.
Bài 4 Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB', B'B và AB, và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC', C'C và AC.
Bài 5 So sánh các tỉ số:
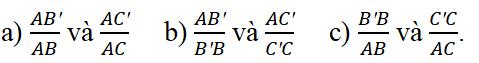
Bài 6 Tính các độ dài x và y trong hình 5.
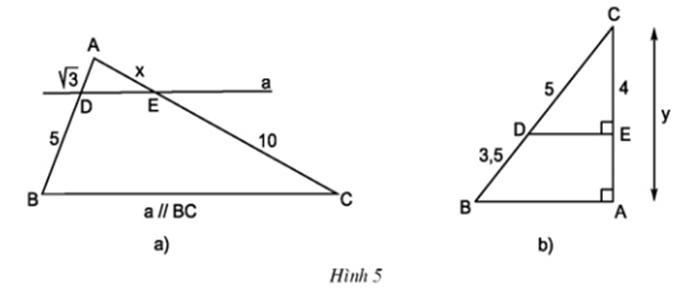
Bài 7 Viết tỉ số của hai đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD = 15 cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
(Ghi nhớ (định nghĩa trang 56 sgk Toán 8 Tập 2)
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.)
Bài 8 Cho biết và CD bằng 12cm. Tính độ dài của AB.
Bài 9 Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.
Bài 10 Cho biết (h.6). Chứng minh rằng:
Bài 11 Tính x trong các trường hợp sau (h.7):
B. Lý thuyết Định lí Ta- let trong tam giác
1. Tỉ số của hai đường thẳng
a) Định nghĩa
+ Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
+ Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là AB/CD.
+ Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào các chọn đơn vị đo
b) Ví dụ
Ví dụ:
Cho AB = 20 cm;CD = 40 cm thì AB/CD = 20/40 = 1/2.
Cho AB = 2 m; CD = 4 m thì AB/CD = 2/4 = 1/2.
2. Đoạn thẳng tỉ lệ
Định nghĩa
+ Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức.
+ Tổng quát: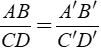
hay
3. Định lý Ta – lét trong tam giác
Định lý Ta – lét:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Tổng quát : Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
Ta có:
Ví dụ: Tính độ dài cạnh AN.
Hướng dẫn:
Ta có MN//BC, áp dụng địnhlý Ta – lét ta có:
AM/MB = AN/NC hay 17/10 = x/9
⇒ x = (17.9)/10 = 15,3
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
