Định lí Talet trong tam giác

Hoài Phạm Thị Thu Ngày: 08-03-2024 Lớp 8

Tải xuống 3 4.1 K 24

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Định lí Talet trong tam giác hình học lớp 8, tài liệu bao gồm 3 trang, tổng hợp đầy đủ lý thuyết và 18 bài tập tự luyện Định lí Talet trong tam giác, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức, chuẩn bị cho các bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Định lí Talet trong tam giác gồm các nội dung sau:

I. Lý thuyết

- Tổng hợp kiến thức trọng tâm cần nhớ về Định lí Talet trong tam giác

II. Bài tập tự luyện

- Gồm 18 bài tập vận dụng giúp học sinh tự rèn luyện cách giải các bài tập Định lí Talet trong tam giác

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

ĐỊNH LÝ TA – LET TRONG TAM GIÁC

I. LÝ THUYẾT

Tỉ số của hai đoạn thẳng. Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Đoạn thẳng tỉ lệ. Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B và C’D nếu có tỉ lệ thức: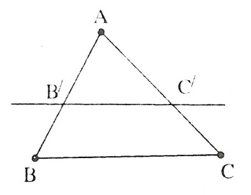

$\frac{A B}{C D} = \frac{A^{'} B^{'}}{C^{'} D^{'}}$ hay $\frac{A B}{A^{'} B^{'}} = \frac{C D}{C^{'} D^{'}}$

Định lý Ta-let trong tam giác. Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Trong hình bên

$\begin{array}{r} Δ ABC \\ \begin{matrix} B^{'} C^{'} / / BC \end{matrix} \end{array}\} \Rightarrow \frac{A B^{'}}{A B} = \frac{A C^{'}}{A C}; \frac{A B^{'}}{B^{'} B} = \frac{A C^{'}}{C^{'} C}; \frac{B^{'} B}{A B} = \frac{C^{'} C}{A C}$

II. BÀI TẬP TỰ LUYỆN

Bài 1. Cho hình bình hành ABCD có AC = 24 cm . Điểm E thuộc cạnh AB sao cho $A E = \frac{1}{2} E B$ . Điểm F là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của AC với DE, DF. Tính các độ dài AI, IK, KC.

Bài 2. Cho tam giác ABC có BC là cạnh lớn nhất. Trên cạnh BC lấy các điểm D, E sao cho BD =BA; CE = CA . Đường thẳng qua D song song với AB cắt AC tại M. Đường thẳng qua E song song với AC cắt AB tại N. Chứng minh AM = AN.

(Tuyển sinh lớp 10 chuyên Toán, TP. Hồ Chí Minh, năm học 2013 - 2014)

Bài 3. Cho tam giác ABC vuông tại A, đường cao AH. Gọi I là trung điểm của AH. Đường vuông góc với BC tại C cắt đường thẳng BI tại D. Chứng minh DA = DC.

Bài 4. Cho hình bình hành ABCD. Trên đường chéo AC lấy một điểm I. Tia DI cắt đường thẳng AB tại M, cắt đường thẳng BC tại N. Chứng minh rằng:

a) $\frac{A M}{A B} = \frac{D M}{D N} = \frac{C B}{C N};$

b) $I D^{2} = I M . I N .$

Bài 5. Cho tam giác ABC vuông tại A. Vẽ về phía ngoài hai tam giác ABD và ACE vuông cân tại B và E. Gọi H là giao điểm của AB và CD; K là giao điểm của AC và BE. Chứng minh rằng:

a) AH = AK;

b) $A H^{2} = B H . C K$ .

Xem thêm

Trang 1

Trang 2

Trang 3

Tài liệu có 3 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

toán 8 Định lý Ta-lét trong tam giác

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm