Với giải Bài 5 trang 103 Toán 12 Tập 2 Cánh diều chi tiết trong Bài tập cuối chương 6 trang 103 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài tập cuối chương 6 trang 103

Bài 5 trang 103 Toán 12 Tập 2: Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7%.

a) Vẽ sơ đồ hình cây biểu thị tình huống trên.

b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.

Lời giải:

a) Xét hai biến cố:

A: “Người được chọn ra không nhiễm bệnh”;

B: “Người được chọn ra có phản ứng dương tính”.

Vì trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh nên P(A) = $\frac{58}{2+58}=\frac{29}{30}$ và P( $\overline{A}$) = $\frac{1}{30}$ .

Do đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7% nên P(B | A) = 7% = 0,07.

Vì đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85% nên P(B | $\overline{A}$ ) = 85% = 0,85.

Sơ đồ hình cây biểu thị tình huống đã cho như sau:

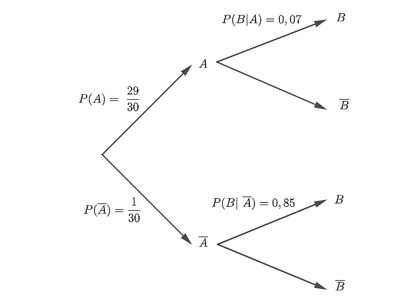
b) Ta thấy xác suất nhiễm bệnh của X khi X là một người trong nhóm bị xét nghiệm có kết quả dương tính chính là P( $\overline{A}$ | B). Áp dụng công thức Bayes, ta có:

P( $\overline{A}$ | B) = $\frac{P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)}{P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)+P\left(A\right)\cdot P\left(B|A\right)}$ = $\frac{\frac{1}{30}\cdot 0,85}{\frac{1}{30}\cdot 0,85+\frac{29}{30}\cdot 0,07}=\frac{85}{288}\approx 0,295$ .

Vậy xác suất để X là người nhiễm bệnh là 0,295.