Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài tập cuối chương 3 trang 57 chi tiết sách Toán 9 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài tập cuối chương 3 trang 57
Bài 1 trang 57 Toán 9 Tập 1: Biểu thức nào dưới đây có giá trị khác với các biểu thức còn lại?
A.
B.
C.
D.
Lời giải:
Ta có = =
Vậy chọn đáp án D
Bài 2 trang 57 Toán 9 Tập 1: Có bao nhiêu số tự nhiên x để là số nguyên?
A. 2
B. 3
C. 4
D. 5
Lời giải:
ĐKXĐ: hay .
Vì x là số tự nhiên nên .
Do đó .
Suy ra có thể bằng: 0; 1; 4; 9; 16
Khi đó x lần lượt là: 16; 15; 12; 7; 0 (TM)
Suy ra bằng: 0; 1; 2; 3; 4.
Vậy có 5 số x thỏa mãn.
Vậy chọn đáp án D.
Bài 3 trang 57 Toán 9 Tập 1: Giá trị của biểu thức bằng
A. 0
B. -2
C. 4
D. 5
Lời giải:
Vậy chọn đáp án A.
Bài 4 trang 57 Toán 9 Tập 1: Đẳng thức nào sau đây không đúng?
A.
B.
C.
D.
Lời giải:
A. (Đúng)
B. (Đúng)
C. (Đúng)
D. (Sai)
Vậy chọn đáp án D.
Bài 5 trang 57 Toán 9 Tập 1: Biết rằng , giá trị của biểu thức bằng
A. 0,0026
B. 0,026
C. 0,26
D. 2,6
Lời giải:
Ta có: suy ra
Vậy chọn đáp án C.
Bài 6 trang 57 Toán 9 Tập 1: Rút gọn biểu thức với , ta có kết quả
A.
B. 15a
C.
D. 7a
Lời giải:
Vậy chọn đáp án C.
Bài 7 trang 57 Toán 9 Tập 1: Cho a = , b = . Rút gọn biểu thức , ta có kết quả
A.
B.
C.
D.
Lời giải:
Thay a = , b = vào ta được:
Vậy chọn đáp án A.
Bài 8 trang 57 Toán 9 Tập 1: Trục căn thức ở mẫu biểu thức với a > 0, ta có kết quả
A.
B.
C.
D.
Lời giải:
Vậy chọn đáp án A.
Bài 9 trang 57 Toán 9 Tập 1: Kết quả của phép tính là
A. 12
B. 18
C. 72
D. 144
Lời giải:
Vậy chọn đáp án B.
Bài 10 trang 57 Toán 9 Tập 1: Rút gọn biểu thức với , , ta có kết quả
A.
B.
C.
D.
Lời giải:
Vậy chọn đáp án D
Bài 11 trang 58 Toán 9 Tập 1: Tìm x, biết:
a) x2 = 10
b)
c) x3 = - 0,027
d)
Lời giải:
a) x2 = 10
b)
c) x3 = - 0,027
d)
Bài 12 trang 58 Toán 9 Tập 1: Biết rằng 1 < a < 5, rút gọn biểu thức
A = .
Lời giải:
A =
Bài 13 trang 58 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:
a)
b)
c) với a > 0, a 1
Lời giải:
a)
b)
c)
với a > 0, a 1
Bài 14 trang 58 Toán 9 Tập 1: Biết rằng a > 0, b > 0 và ab = 16. Tính giá trị của biểu thức .
Lời giải:
Thay ab = 16 vào ta có:
Bài 15 trang 58 Toán 9 Tập 1: Tính .
Lời giải:
Bài 16 trang 58 Toán 9 Tập 1: Một trục số được vẽ trên lưới ô vuông như Hình 1.
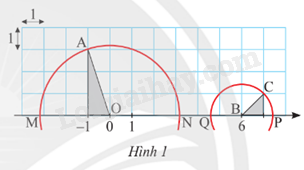
a) Đường tròn tâm O bán kính OA cắt trục số tại hai điểm M và N. Hai điểm M và N biểu diễn hai số thực nào?
b) Đường tròn tâm B bán kính BC cắt trục số tại hai điểm P và Q. Hai điểm P và Q biểu diễn hai số thực nào?
Lời giải:
a) Ta có OM = OA = (Áp dụng định lý Pythagore vào tam giác vuông)
Vậy điểm M và N biểu diễn hai số thực lần lượt là - và .
b) Ta có BP = BC = (Áp dụng định lý Pythagore vào tam giác vuông)
Vậy điểm Q và P biểu diễn hai số thực lần lượt là - và .
a) Tính thể tích của hình hộp chữ nhật đó.
b) Tính diện tích xung quanh của hình hộp chữ nhật đó.
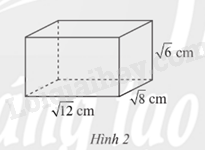
Lời giải:
a) Thể tích của hình hộp chữ nhật đó là:
..= = 24 (cm3)
b) Diện tích xung quanh của hình hộp chữ nhật đó là:
2( +).= (cm2).
Bài 18 trang 58 Toán 9 Tập 1: Rút gọn các biểu thức sau:
a) với a > 0
b) với
Lời giải:
a) với a > 0
b) với
Bài 19 trang 58 Toán 9 Tập 1: Cho biểu thức với a > 0 và a 1.
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi a = 0,25
Lời giải:
b) Thay a = 0,25 vào P = ta có:
P = .
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông