Với lời giải Toán 11 trang 47 Tập 2 chi tiết trong Bài 3: Hàm số mũ. Hàm số lôgarit sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 1 trang 47 Toán 11 Tập 2: Tìm tập xác định của các hàm số:

a) y = 12^x;

b) y = log₅(2x – 3);

c) $y={\text{log}}_{\frac{1}{5}}\left(-x^2+4\right)$ .

Lời giải:

a) Hàm số y = 12^x xác định với mọi x nên tập xác định D = ℝ.

b) Hàm số y = log₅(2x – 3) xác định khi 2x – 3 > 0 hay $x>\frac{3}{2}$

Vậy tập xác định của hàm số trên là $D=\left(\frac{3}{2};+\infty \right)$ .

c) Hàm số $y={\text{log}}_{\frac{1}{5}}\left(-x^2+4\right)$ xác định khi –x² + 4 > 0, hay x² < 4 nên –2 < x < 2

Vậy tập xác định của hàm số trên là D = (–2; 2).

Bài 2 trang 47 Toán 11 Tập 2: Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?

a) $y={\left(\frac{\sqrt{3}}{2}\right)}^x;$ b) $y={\left(\frac{\sqrt[3]{26}}{3}\right)}^x;$

c) y = log_πx; d) $y={\text{log}}_{\frac{\sqrt{15}}{4}}x.$

Lời giải:

a) Hàm số $y={\left(\frac{\sqrt{3}}{2}\right)}^x$ có tập xác định D = ℝ.

Do $0<\frac{\sqrt{3}}{2}<1$ nên hàm số $y={\left(\frac{\sqrt{3}}{2}\right)}^x$ nghịch biến ℝ.

b) Hàm số $y={\left(\frac{\sqrt[3]{26}}{3}\right)}^x$ có tập xác định D = ℝ.

Do $0<\frac{\sqrt[3]{26}}{3}<1$ nên hàm số $y={\left(\frac{\sqrt[3]{26}}{3}\right)}^x$ nghịch biến trên ℝ.

c) Hàm số y = log_πx có tập xác định là D = (0; +∞).

Do π > 1nên hàm số y = log_πx đồng biến trên (0; +∞).

d) Hàm số $y={\text{log}}_{\frac{\sqrt{15}}{4}}x$ có tập xác định là D = (0; +∞).

Do $0<\frac{\sqrt{15}}{4}<1$ nên hàm số $y={\text{log}}_{\frac{\sqrt{15}}{4}}x$ nghịch biến trên (0; +∞).

Bài 3 trang 47 Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số:

a) y = 4^x;b) $y={\text{log}}_{\frac{1}{4}}x$ .

Lời giải:

a) Vì hàm số y = 4^x có cơ số 4 > 1 nên ta có bảng biến thiên như sau:

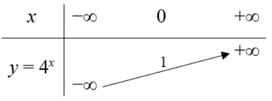
Đồ thị hàm số y = 4^x là đường thẳng đi qua các điểm $A\left(-1;\frac{1}{4}\right),B\left(0;1\right),$ $C\left(\frac{1}{2};2\right),D\left(1;4\right),E\left(\frac{3}{2};8\right)$ như hình vẽ:

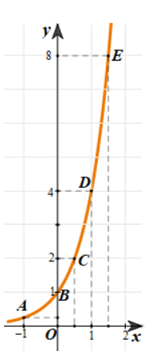
b) Vì hàm số $y={\text{log}}_{\frac{1}{4}}x$ có cơ số $\frac{1}{4}<1$ nên ta có bảng biến thiên như sau:

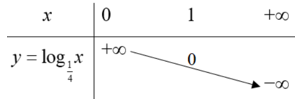
Đồ thị hàm số $y={\text{log}}_{\frac{1}{4}}x$ là đường thẳng đi qua các điểm $M\left(\frac{1}{4};1\right),N\left(1;0\right),$ $P\left(2;\frac{-1}{2}\right),$ $Q\left(4;-1\right),R\left(8;-\frac{3}{2}\right)$ như hình vẽ:

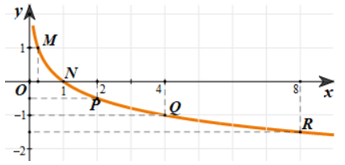
Bài 4 trang 47 Toán 11 Tập 2: Ta coi năm lấy làm mốc để tính dân số của một vùng (hoặc một quốc gia) là năm 0. Khi đó, dân số của quốc gia đó ở năm thứ t là hàm số theo biến t được cho bởi công thức: S = A.e^rt, trong đó A là dân số của vùng (hoặc quốc gia) đó ở năm 0 và r là tỉ lệ tăng dân số hằng năm (Nguồn: Giải tích 12, NXBGD Việt Nam, 2021). Biết rằng dân số Việt Nam năm 2021 ước tính là 98 564 407 người và tỉ lệ tăng dân số 0,93%/năm (Nguồn: https://danso.org/viet–nam. Giả sử tỉ lệ tăng dân số hằng năm là như nhau tính từ năm 2021, nêu dự đoán dân số Việt Nam năm 2030 (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Ta có: S = A . e^rt

Trong đó:

⦁S là dân số của Việt Nam năm 2030 (cần dự đoán);

⦁A là dân số của Việt Nam năm 2021, A = 98564407 người;

⦁r là tỉ lệ tăng dân số hàng năm, r = 0,93%;

⦁t là số năm từ năm 2021 đến năm 2030, tức là t = 2030 – 2021 = 9 năm.

Thay các giá trị vào công thức, ta có:

S = 98 564 407 . e^0,93%.9 = 98 564 407 . e^0,0837 ≈ 107 169 341 (người).

Vậy dự đoán dân số Việt Nam năm 2030 là khoảng 107 169 341 người.

Bài 5 trang 47 Toán 11 Tập 2: Các nhà tâm lí học sử dụng mô hình hàm số mũ để mô phỏng quá trình học tập của một học sinh như sau: f(t) = c(1 – e^–kt), trong đó c là tổng số đơn vị kiến thức học sinh phải học, k (kiến thức/ngày) là tốc độ tiếp thu của học sinh, t (ngày) là thời gian học và f(t) là số đơn vị kiến thức học sinh đã học được (Nguồn: R.I. Charles et al., Algebra 2, Pearson). Giả sử một em học sinh phải tiếp thu 25 đơn vị kiến thức mới. Biết rằng tốc độ tiếp thu của em học sinh là k = 0,2. Hỏi em học sinh sẽ học được (khoảng) bao nhiêu đơn vị kiến thức mới sau 2 ngày? Sau 8 ngày? (Làm tròn kết quả đến hàng đơn vị).

Lời giải:

Để tính số đơn vị kiến thức học sinh đã học được sau một số ngày nhất định, ta chỉ cần thay giá trị của t vào công thức f(t) = c(1 – e^–kt) với c = 25 và k = 0,2.

Lúc này ta có f(t) = 25(1 – e^−0,2t).

⦁Số đơn vị kiến thức học sinh đã học được sau 2 ngày:

Thay t = 2 vào công thức f(t) = 25(1 – e^−0,2t) ta có:

f(2) = 25(1 – e^–0,2.2) ≈ 8 (đơn vị kiến thức).

⦁Số đơn vị kiến thức học sinh đã học được sau 8 ngày:

Thay t = 8 vào công thức f(t) = 25(1 – e^−0,2t) ta có:

f(8) = 25(1 – e^–0,2.8) ≈ 20 (đơn vị kiến thức).

Bài 6 trang 47 Toán 11 Tập 2: Chỉ số hay độ pH của một dung dịch được tính theo công thức: pH = – log[H⁺]. Phân tích nồng độ ion hydrogen [H⁺] trong hai mẫu nước sông, ta có kết quả sau:

Mẫu 1: [H⁺] = 8 . 10^–7; Mẫu 2: [H⁺] = 2 . 10^–9.

Không dùng máy tính cầm tay, hãy so sánh độ pH của hai mẫu nước trên.

Lời giải:

Mẫu 1:

pH = – log[H⁺] = –log(8 . 10^–7) = – (log8 + log10^–7)

= – log8 – log10^–7= – log8 + 7log10

= – log2³ + 7 = – 3log2 + 7.

Mẫu 2:

pH = – log[H⁺] = –log(2 . 10^–9) = – (log2 – log10^–9)

= – log2 – log10^–9= – log2 + 9log10

= – log2 + 9.

Vì 3log2 > log2 nên – 3log2 < – log2

Suy ra – 3log2 + 7 < – log2 + 7

Hay – 3log2 + 7 < – log2 + 9

Do đó độ pH của mẫu 1nhỏ hơn độ pH của mẫu 2.

Bài 7 trang 47 Toán 11 Tập 2: Cô Yên gửi 10 triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất 6% /năm. Giả sử qua các năm thì lãi suất không thay đổi và cô Yên không gửi thêm tiền vào mỗi năm. Để biết sau y (năm) thì tổng số tiền cả vốn và lãi có được là x (đồng), cô Yên sử dụng công thức $y={\text{log}}_{\mathrm{1,06}}\left(\frac{x}{10}\right)$ . Hỏi sau ít nhất bao nhiêu năm thì cô Yên có thể rút ra số tiền 15 triệu đồng từ tài khoản tiết kiện đó (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Để cô Yên có thể rút ra số tiền 15 triệu đồng từ tài khoản tiết kiện đó thì x = 15.

Khi đó ta có $y={\text{log}}_{\mathrm{1,06}}\left(\frac{x}{10}\right)={\log }_{\mathrm{1,06}}\frac{15}{10}\approx 7$

Vậy sau ít nhất 7 năm thì cô Yên có thể rút ra được số tiền 15 triệu đồng từ tài khoản tiết kiệm đó.