Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 2: Phép tính lôgarit chi tiết sách Toán 11 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 2: Phép tính lôgarit

Giải Toán 11 trang 34 Tập 2

Câu hỏi khởi động trang 34 Toán 11 Tập 2: Chỉ số hay độ pH của một dung dịch được tính theo công thức: pH = – log[H⁺] với [H⁺] là nồng độ ion hydrogen. Người ta đo được nồng độ ion hydrogen của một cốc nước cam là 10^–4, nước dừa là 10^–5 (nồng độ tính bằng molL^–1). Làm thế nào để tính được độ pH của cốc nước cam, nước dừa đó?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Độ pH của cốc nước cam là: pH = –log[H⁺] = –log10^–4 = –(–4) = 4;

Độ pH của cốc nước dừa là:pH = –log[H⁺] = –log10^–5 = –(–5) = 5.

I. Khái niệm Lôgarit

Hoạt động 1 trang 34 Toán 11 Tập 2: a) Tìm x trong mỗi trường hợp sau: $3^x=9;3^x=\frac{1}{9}.$

b) Có bao nhiêu số thực x sao cho 3^x = 5?

Lời giải:

a) Ta có:

⦁ 3^x = 9 ⇔ 3^x = 3² ⇔ x = 2;

⦁ $3^x=\frac{1}{9}\iff 3^x=3^{-2}\iff x=-2.$

b) Có đúng một số thực x sao cho 3^x = 5.

Luyện tập 1 trang 34 Toán 11 Tập 2: Tính:

a) log₃81; b) ${\log }_{10}\frac{1}{100}.$

Lời giải:

a) log₃81 = 4 vì 3⁴ = 81;

b) ${\log }_{10}\frac{1}{100}=-2$ vì ${10}^{-2}=\frac{1}{100}.$

Giải Toán 11 trang 35 Tập 2

Hoạt động 2 trang 35 Toán 11 Tập 2: Cho a > 0, a ≠ 1. Tính:

a) log_a1;

b) log_aa;

c) log_a a^c;

d) $a^{{\log }_{a}b}$ với b > 0.

Lời giải:

Với a > 0, a ≠ 1 ta có:

a) log_a1 = 0 vì a⁰ = 1;

b) log_aa = 1 vì a¹ = a;

c) log_a a^c = c vì a^c = a^c;

d) Với b > 0, đặt log_ab = c, suy ra a^c = b

Ta có $a^{{\log }_{a}b}=a^c=b$

Vậy $a^{{\log }_{a}b}=b$ (với b > 0).

Luyện tập 2 trang 35 Toán 11 Tập 2: Tính:

a) ${\log }_4\sqrt[5]{16};$ b) ${36}^{{\log }_{6}8}.$

Lời giải:

Ta có:

a) ${\log }_4\sqrt[5]{16}={\log }_4{16}^{\frac{1}{5}}={\log }_4{4}^{\frac{2}{5}}=\frac{2}{5};$

b) ${36}^{{\log }_{6}8}={\left(6^2\right)}^{{\log }_{6}8}={\left(6^{{\log }_{6}8}\right)}^2=8^2=64.$

Luyện tập 3 trang 35 Toán 11 Tập 2: Giải bài toán được nêu ở phần mở đầu.

Lời giải:

Độ pH của cốc nước cam là: pH = –log[H⁺] = –log10^–4 = –(–4) = 4;

Độ pH của cốc nước dừa là:pH = –log[H⁺] = –log10^–5 = –(–5) = 5.

II. Một số tính chất của phép tính Lôgarit

Hoạt động 3 trang 35 Toán 11 Tập 2: Cho m = 2⁷, n = 2³.

a) Tính log₂(mn); log₂m + log₂n và so sánh các kết quả đó.

b) Tính ${\log }_2\left(\frac{m}{n}\right);$ log₂m – log₂n và so sánh các kết quả đó.

Lời giải:

a) Ta có:

⦁ log₂(mn) = log₂ (2⁷ . 2³) = log₂ 2¹⁰ = 10;

⦁ log₂m + log₂n = log₂ 2⁷ + log₂ 2³ = 7 + 3 = 10.

Suy ra log₂(mn) = log₂m + log₂n.

b) Ta có:

⦁ ${\log }_2\left(\frac{m}{n}\right)={\log }_2\left(\frac{2^7}{2^3}\right)={\log }_2{2}^4=4;$

⦁ log₂m – log₂n = log₂ 2⁷ – log₂ 2³ = 7 – 3 = 4.

Suy ra ${\log }_2\left(\frac{m}{n}\right)={\log }_{2}m-{\log }_{2}n.$

Giải Toán 11 trang 36 Tập 2

Luyện tập 4 trang 36 Toán 11 Tập 2: Tính:

a) $\ln \left(\sqrt{5}+2\right)+\ln \left(\sqrt{5}-2\right);$

b) log400 – log4;

c) ${\log }_{4}8+{\log }_{4}12+{\log }_4\frac{32}{3}.$

Lời giải:

a) $\ln \left(\sqrt{5}+2\right)+\ln \left(\sqrt{5}-2\right)=\ln \left(\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)\right)$$=\ln \left(5-4\right)=\ln 1=0;$

b) $\log 400-\log 4=\log \frac{400}{4}$$=\log 100=\log {10}^2=2;$

c) ${\log }_{4}8+{\log }_{4}12+{\log }_4\frac{32}{3}={\log }_4\left(8\cdot 12\cdot \frac{32}{3}\right)$$={\log }_4\left(32\cdot 32\right)={\log }_4{4}^5=5.$

Hoạt động 4 trang 36 Toán 11 Tập 2: Cho a > 0, a ≠1, b > 0, α là một số thực.

a) Tính $a^{{\log }_a{b}^{\alpha }}$ và $a^{\alpha {\log }_{a}b}$ .

b) So sánh ${\log }_a{b}^{\alpha }$ và $\alpha {\log }_{a}b$.

Lời giải:

a) Với a > 0, a ≠1, b > 0, ta có:

⦁ Đặt $a^{{\log }_a{b}^{\alpha }}=c$ suy ra ${\log }_a{a}^{{\log }_a{b}^{\alpha }}={\log }_{a}c$ hay ${\log }_{a}c={\log }_a{b}^{\alpha },$ do đó $c=b^{\alpha }$

Vậy $a^{{\log }_a{b}^{\alpha }}=b^{\alpha }.$

⦁ Đặt $a^{\alpha {\log }_{a}b}=c$ suy ra ${\log }_a{a}^{\alpha {\log }_{a}b}={\log }_{a}c$ hay ${\log }_{a}c=\alpha {\log }_{a}b$

Do đó ${\log }_{a}c={\log }_a{b}^{\alpha }$ nên $c=b^{\alpha }$

Vậy $a^{\alpha {\log }_{a}b}=b^{\alpha }.$

b) Vì $a^{{\log }_a{b}^{\alpha }}=b^{\alpha };a^{\alpha {\log }_{a}b}=b^{\alpha }$

Nên $a^{{\log }_a{b}^{\alpha }}=a^{\alpha {\log }_{a}b}$

Suy ra ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b.$

Luyện tập 5 trang 36 Toán 11 Tập 2: Tính: $2{\log }_{3}5-{\log }_{3}50+\frac{1}{2}{\log }_{3}36$ .

Lời giải:

Ta có:

$2{\log }_{3}5-{\log }_{3}50+\frac{1}{2}{\log }_{3}36$

$={\log }_3{5}^2-{\log }_{3}50+{\log }_3{36}^{\frac{1}{2}}$

$={\log }_{3}25-{\log }_{3}50+{\log }_{3}6$

$={\log }_3\left(\frac{25}{50}\cdot 6\right)={\log }_{3}3=1.$

Giải Toán 11 trang 37 Tập 2

Hoạt động 5 trang 37 Toán 11 Tập 2: Cho ba số thực dương a, b, c với a ≠ 1, b ≠ 1.

a) Bằng cách sử dụng tính chất $c=b^{{\log }_{b}c},$ chứng tỏ rằng log_ac = log_bc . log_ab;

b) So sánh log_bc và $\frac{{\log }_{a}c}{{\log }_{a}b}.$

Lời giải:

a) Với a, b, c > 0 và a ≠ 1, b ≠ 1, ta có:

$$\begin{gathered} c=b^{{\log }_{b}c}\iff {\log }_{a}c={\log }_a{b}^{{\log }_{b}c} \\ \iff {\log }_{a}c={\log }_{b}c\cdot {\log }_{a}b \end{gathered}$$

Vậy log_ac = log_bc . log_ab.

b) Từ log_ac = log_bc . log_ab suy ra ${\log }_{b}c=\frac{{\log }_{a}c}{{\log }_{a}b}.$

Luyện tập 6 trang 37 Toán 11 Tập 2: Tính: $5^{{\log }_{125}64}.$

Lời giải:

Ta có: $5^{{\log }_{125}64}=5^{{\log }_{5^3}64}=5^{\frac{1}{3}{\log }_{5}64}$$=5^{{\log }_5\sqrt[3]{64}}=5^{{\log }_{5}4}=4.$

III. Sử dụng máy tính cầm tay để tính Lôgarit

Giải Toán 11 trang 38 Tập 2

Luyện tập 7 trang 38 Toán 11 Tập 2: Sử dụng máy tính cầm tay để tính: log₇19; log₁₁26.

Lời giải:

Ta sử dụng máy tính cầm tay để tính logarit như sau (lấy kết quả với 4 chữ số ở phần thập phân):

Chú ý: Với máy tính không có phím 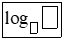thì để tính log₇19, ta có thể dùng công thức đổi cơ số để đưa về cơ số 10 hoặc cơ số ℯ như sau:

$lo{g}_{7}19=\frac{log19}{log7}$ hoặc $lo{g}_{7}19=\frac{\ln 19}{\ln 7},$ sau đó dùng máy tính để tính như dưới đây:

Do đó log₇19 ≈ 1,5131.

Tương tự, ta cũng tính được log₁₁26 ≈ 1,3587.

Vậy log₇19 ≈ 1,5131 và log₁₁26 ≈ 1,3587.

Bài tập

Bài 1 trang 38 Toán 11 Tập 2: Tính:

a) log₁₂12³; b) log_0,50,25; c) log_aa^–3 (a > 0, a ≠ 1).

Lời giải:

a) log₁₂12³ = 3;

b) log_0,50,25 = log_0,50,5² = 2;

c) log_aa^–3 = –3 (với a > 0, a ≠ 1).

Bài 2 trang 38 Toán 11 Tập 2: Tính:

a) $8^{{\log }_{2}5};$ b) ${\left(\frac{1}{10}\right)}^{\log 81};$ c) $5^{{\log }_{25}16}.$

Lời giải:

a) $8^{{\log }_{2}5}={\left(2^3\right)}^{{\log }_{2}5}=2^{3{\log }_{2}5}=2^{{\log }_2{5}^3}$$=5^3=125;$

b) ${\left(\frac{1}{10}\right)}^{\log 81}={10}^{-\log 81}={10}^{\log {81}^{-1}}$$={81}^{-1}=\frac{1}{81};$

c) $5^{{\log }_{25}16}=5^{{\log }_{5^2}16}=5^{\frac{1}{2}{\log }_{5}16}$$=5^{{\log }_5{16}^{\frac{1}{2}}}={16}^{\frac{1}{2}}=\sqrt{16}=4.$

Bài 3 trang 38 Toán 11 Tập 2: Cho log_ab = 2. Tính:

a) log_a(a²b³);

b) ${\log }_a\frac{a\sqrt{a}}{b\sqrt[3]{b}};$

c) ${\log }_a\left(2b\right)+{\log }_a\left(\frac{b^2}{2}\right).$

Lời giải:

a) log_a(a²b³) = log_aa² + log_ab³ = 2log_aa + 3log_ab = 2 . 1 + 3 . 2 = 8;

b) ${\log }_a\frac{a\sqrt{a}}{b\sqrt[3]{b}}={\log }_a{\left(\sqrt{a}\right)}^3-{\log }_a{\left(\sqrt[3]{b}\right)}^4$

$={\log }_a{a}^{\frac{3}{2}}-{\log }_a{b}^{\frac{4}{3}}$

$=\frac{3}{2}{\log }_{a}a-\frac{4}{3}{\log }_{a}b$

$=\frac{3}{2}\cdot 1-\frac{4}{3}\cdot 2=\frac{3}{2}-\frac{8}{3}=-\frac{7}{6};$

c) ${\log }_a\left(2b\right)+{\log }_a\left(\frac{b^2}{2}\right)={\log }_a\left(2b\cdot \frac{b^2}{2}\right)$$={\log }_a{b}^3=3{\log }_{a}b=3\cdot 2=6.$

Bài 4 trang 38 Toán 11 Tập 2: Cho hai số thực dương a, b thoả mãn a³b² = 100. Tính giá trị của biểu thức P = 3log a + 2log b.

Lời giải:

Ta có: P = log a³ + log b² = log a³b² = log 100 = 10.

Bài 5 trang 38 Toán 11 Tập 2: Trong nuôi trồng thuỷ sản, độ pH của môi trường nước sẽ ảnh hưởng đến sức khoẻ và sự phát triển của thuỷ sản. Độ pH thích hợp cho nước trong đầm nuôi tôm sú là từ 7,2 đến 8,8 và tốt nhất là trong khoảng từ 7,8 đến 8,5. Phân tích nồng độ [H⁺] trong một đầm nuôi tôm sú, ta thu được [H⁺] = 8 . 10^–8 (Nguồn: https://nongnghiep.farmvina.com). Hỏi độ pH của đầm đó có thích hợp cho tôm sú phát triển không?

Lời giải:

Vì pH = – log [H⁺] = – log 8 . 10^–8 ≈ 7,1

Suy ra độ pH không phù hợ cho tôm sú phát triển.

Bài 6 trang 38 Toán 11 Tập 2: Một vi khuẩn có khối lượng khoảng 5 . 10^–13 gam và cứ 20 phút vi khuẩn đó tự nhân đôi một lần (Nguồn: Câu hỏi và bài tập vi sinh học, NXB ĐHSP, 2008). Giả sử các vi khuẩn được nuôi trong các điều kiện sinh trưởng tối ưu và mỗi con vi khuẩn đều tồn tại trong ít nhất 60 giờ. Hỏi sau bao nhiêu giờ khối lượng do tế bào vi khuẩn này sinh ra sẽ đạt tới khối lượng của Trái Đất (lấy khối lượng của Trái Đất là 6 . 10²⁷ gam) (làm tròn kết quả đến hàng đơn vị)?

Lời giải:

Số lượng tế bào đạt đến khối lượng Trái Đất là:

N = 6 . 10²⁷ . 10³ : 5 . 10^–13 = 1,2 . 10²⁷

Số lần phân chia: N = N₀ . 2ⁿ

Suy ra $n=\frac{\log N-\log N_0}{\log 2}=\frac{\log {\mathrm{1,2.10}}^{27}-\log {5.10}^{-13}}{\log 2}\approx \mathrm{97,6}$

Thời gian cần thiết là: 97,6 : 3 = 32,5 (giờ)

Vậy sau 32,5 giờ khối lượng do tế bào vi khuẩn này sinh ra sẽ đạt tới khối lượng của Trái Đất.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Phép tính lũy thừa với số mũ thực

Bài 2: Phép tính lôgarit

Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 4: Phương trình mũ, bất phương trình mũ và lôgarit

Bài tập cuối chương 6

Lý thuyết Phép tính lôgarit

1. Khái niệm lôgarit

a) Định nghĩa

Với a > 0, a $\ne$ 1 và b > 0, ta có: $c={\log }_{a}b\iff a^c=b$. Ngoài ra:

- Lôgarit thập phân của b là lôgarit cơ số 10 của số thực dương b:

$c=\log b\iff {10}^c=b$

- Lôgarit tự nhiên của b là lôgarit cơ số e của số thực dương b:

$c=\ln b\iff e^c=b$.

b) Tính chất

Với a > 0, a $\ne$ 1 và b > 0, ta có:

${\log }_{a}1=0$; ${\log }_{a}a=1$; ${\log }_a{a}^c=c$; $a^{{\log }_{a}b}=b$.

2. Một số tính chất của phép tính lôgarit

Trong mục này, ta xét a > 0, a $\ne$ 1 và b > 0.

a) Lôgarit của một tích, một thương

Với m > 0, n > 0, ta có:

• ${\log }_a\left(mn\right)={\log }_{a}m+{\log }_{a}n$;
• ${\log }_a\left(\frac{m}{n}\right)={\log }_{a}m-{\log }_{a}n$.

Nhận xét: ${\log }_a\left(\frac{1}{b}\right)=-{\log }_{a}b$.

b) Lôgarit của một lũy thừa

Với mọi số thực $\alpha$, ta có: ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$.

Nhận xét: Với mọi số nguyên dương $n\ge 2$, ta có: ${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$.

c) Đổi cơ số của lôgarit

Với a, b là hai số thực dương khác 1 và c là số thực dương, ta có: ${\log }_{b}c=\frac{{\log }_{a}c}{{\log }_{a}b}$.

Nhận xét: Với a, b là hai số thực dương khác 1, c > 0 và $\alpha \ne 0$, ta có những công thức sau:

• ${\log }_{a}b.{\log }_{b}c={\log }_{a}c$;
• ${\log }_{a}b=\frac{1}{{\log }_{b}a}$;
• ${\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b$.