Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 3: Tính chất đường phân giác của tam giác chi tiết sách Toán 8 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 3: Tính chất đường phân giác của tam giác
Lời giải:
Dựa vào độ dài các cạnh ở trên hình vẽ, ta có:
Do đó, đường phân giác AD của tam giác ABC chia cạnh đối diện BC thành hai đoạn BD. CD tỉ lệ với hai đoạn thẳng AB, AC trong hình.
1. Tính chất đường phân giác của tam giác
a) Tam giác BAE cân tại A.
b) .
Lời giải:
a) Ta có: BE // AD suy ra (hai góc đồng vị), (hai góc so le trong)
AD là tia phân giác góc nên
Do đó: suy ra tam giác BAE cân tại A
b) Xét tam giác BCE có AD // BE, theo định lí Thalès, ta có:
Mà AE = AB (do tam giác ABE cân tại A)
Do đó:
2. Áp dụng tính chia tỉ lệ của đường phân giác của tam giác
Thực hành trang 56 Toán 8 Tập 2: Tính độ dài cạnh MQ của tam giác MPQ trong Hình 6.
Lời giải:
Trong tam giác MPQ, ta có MN là đường phân giác góc M nên ta có
hay
Do đó
Bài tập
Bài 1 trang 56 Toán 8 Tập 2: Tính độ dài x trong Hình 7.
Lời giải:
a) Trong tam giác ABC, ta có AD là đường phân giác góc A nên ta có
hay
Suy ra
b) Trong tam giác EFG, ta có EH là đường phân giác góc E nên ta có
hay
Suy ra
c) Trong tam giác PQR, ta có RS là đường phân giác góc R nên ta có
hay .
Suy ra
a) Tính độ dài các đoạn thẳng DB và DC.
b) Tính tỉ số diện tích giữa ΔADB và ΔADC.
Lời giải:
a) Tam giác ABC có AD là đường phân giác nên
Áp dụng tính chất dãy tỉ số bằng nhau, ta có
Nên
Vậy
b) Vẽ AH ⊥ BC tại H
.
a) Tính độ dài các đoạn thẳng DB, DC và DE.
b) Chứng minh ABC là tam giác vuông. Tính diện tích tam giác ABC.
c) Tính diện tích các tam giác ADB, ADE và DCE.
Lời giải:
a) Trong tam giác ABC, ta có: AD là tia phân giác của .
Suy ra: (tính chất đường phân giác)
Mà AB = 15 cm; AC = 20 cm.
Nên
Suy ra: (tính chất tỉ lệ thức)
Suy ra:
Nên:
Do đó
Xét tam giác ABC có DE // AB, theo hệ quả định lí Thalès, ta có:
Vậy .
b) Xét tam giác ABC ta có: AB = 15 cm, AC = 20 cm, BC = 25 cm.
Nên suy ra tam giác ABC vuông tại A.
Khi đó, ta có:
Vậy diện tích tam giác ABC là 150 cm2.
c) Kẻ AH ⊥ BC ta có:
Suy ra
Suy ra
Vậy
a) Tính BC, DB, DC.
b) Vẽ đường cao AH. Tính AH, HD và AD.
Lời giải:
a) Tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:
suy ra BC = 5 cm
AD là tia phân giác góc A nên suy ra
Do đó
Vậy BC = 5 cm, ,
b) Ta có:
Tam giác ABH vuông tại H nên
Ta có: (cm)
Tam giác ABH vuông tại H nên
Vậy , , .
Lời giải:
• Xét tam giác ABM có MD là đường phân giác suy ra .
• Xét tam giác ACM có ME là đường phân giác suy ra .
Mà MB = MC, do đó: , theo định lí Thalès đảo ta có: DE // BC.
Lý thuyết Tính chất đường phân giác của tam giác
1. Tính chất đường phân giác của tam giác
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
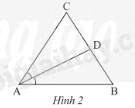
AD là đường phân giác của góc A trong ,
Ví dụ:
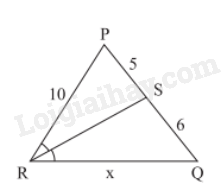
RS là tia phân giác của góc . Sử dụng tính chất đường phân giác, ta có:
Vậy độ dài đoạn thẳng RQ là 12.