Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 39: Hình chóp tứ giác đều chi tiết sách Toán 8 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 39: Hình chóp tứ giác đều
Lời giải:
Sau bài học này, ta sẽ giải quyết bài toán trên như sau:
Vì kim tự tháp Kheops có dạng hình chóp tứ giác đều nên thể tích của nó là:
(m3).
1. Hình chóp tứ giác đều
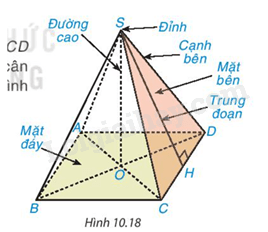
Gọi tên đỉnh, các cạnh bên của hình chóp.
Lời giải:
– Đỉnh: S.
– Các cạnh bên: SD, SC, SA, SB.
HĐ2 trang 117 Toán 8 Tập 2: Gọi tên đường cao, một trung đoạn của hình chóp trong Hình 10.18.
Lời giải:
Đường cao: SO.
Một trung đoạn: SH.
HĐ3 trang 117 Toán 8 Tập 2: Gọi tên các mặt bên và mặt đáy của hình chóp trong Hình 10.18.
Lời giải:
Các mặt bên: SCD, SAB, SBC, SAD.
Mặt đáy: ABCD.
2.Diện tích xung quanh và thể tích của hình chóp tứ giác đều
Lời giải:
Nửa chu vi đáy của chiếc hộp gỗ là: (4 . 2) : 2 = 4 (m).
Diện tích xung quanh của chiếc hộp gỗ hình chóp là: Sxq = p . d = 3 . 4 = 12 (m2).
Chi phí bác Khôi phải trả là: 30 000 . 12 = 360 000 (đồng).
a) Thể tích không khí trong lều là bao nhiêu?
b) Biết lều phủ vải bốn phía và cả mặt tiếp đất. Tính diện tích vải bạt cần dùng (coi mép nối không đáng kể), biết rằng người ta đo được chiều cao của mỗi mặt bên xuất phát từ đỉnh của chiếc lều là 2,24 m.
Lời giải:
a) Diện tích mặt đáy của lều là: Sđ = 2 . 2 = 4 (m2).
Ta có h = SO = 2 m.
Thể tích không khí trong lều chính bằng thể tích của hình chóp S.ABCD và là:
V = Sđh = . 4 . 2 = (m3).
b) Nửa chu vi mặt đáy của lều là: p = (2 . 4) : 2 = 4 (m).
Trung đoạn d = SH = 2,24 m.
Diện tích xung quanh của lều là Sxq = p.d = 4 . 2,24 = 8,96 (m2).
Diện tích vải bạt cần dùng là: S = Sxq + Sđ = 8,96 + 4 = 12,96 (m2).
Vận dụng trang 119 Toán 8 Tập 2: Em hãy giải bài toán mở đầu.
bài toán mở đầu: Kim tự tháp Kheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước Công nguyên là một trong những công trình cổ nhất và duy nhất còn tồn tại trong số bảy kì quan thế giới cổ đại. Kim tự tháp này có dạng hình chóp tứ giác đều cao 147 m, cạnh đáy dài 230 m (H.10.17). Kim tự tháp Kheops có thể tích bằng bao nhiêu?
Lời giải:
Vì kim tự tháp Kheops có dạng hình chóp tứ giác đều nên thể tích của nó là:
(m3).
Bài tập
Lời giải:
– Đỉnh: S.
– Các cạnh bên: SE, SF, SG, SH.
– Các mặt bên: SEF, SFG, SGH, SEH.
– Mặt đáy: EFGH.
– Đường cao: SI.
– Một trung đoạn: SK.
Lời giải:
Hình b) gấp lại thành một hình chóp tứ giác đều.
Hình a) không thỏa mãn do chỉ có 3 mặt bên, hình c) không thỏa mãn do khi gấp lại ta thấy có 2 mặt bên trùng nhau nên không tạo thành 4 mặt bên.
Lời giải:
Học sinh tự thực hiện theo hướng dẫn ở đề bài.
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Lời giải:
a) Nửa chu vi mặt đáy ABCD của hình chóp là: p = (10 . 4) : 2 = 20 (cm).
Diện tích xung quanh của hình chóp S.ABCD là
Sxq = p . d = 20 . 13 = 260 (cm2).
b) Diện tích mặt đáy ABCD là: Sđ = 10 . 10 = 100 (cm2).
Diện tích toàn phần của hình chóp S.ABCD là:
Stp = Sxq + Sđ = 260 + 100 = 360 (cm2).
Lời giải:
Diện tích đáy là: 3 . 3 = 9 (cm2).
Thể tích một chiếc bánh ít là: (cm3).
Lời giải:
Thể tích của hình hộp chữ nhật là: Vhhcn = 40 . 40 . 25 = 40 000 (cm3).
Diện tích đáy của hình chóp tứ giác đều là: S = 40 . 40 = 1 600 (cm2).
Thể tích của khối chóp tứ giác đều là:
(cm3).
Thể tích của khối bê tông là:
V = Vhhcn + Vhc = 40 000 + ≈ 93 333,3 (cm3).
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Một vài ứng dụng của hàm số bậc nhất trong tài chính
Lý thuyết Hình chóp tứ giác đều
1. Định nghĩa
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của mặt đáy (giao điểm hai đường chéo)
2. Diện tích xung quanh và thể tích của hình chóp tứ giác đều
a. Diện tích xung quanh của hình chóp tứ giác đều
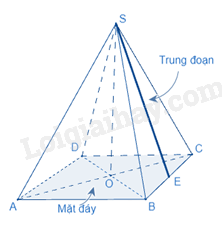
Diện tích xung quanh, kí hiệu là của hình chóp tứ giác đều được tính theo công thức:
,
trong đó p là nửa chu vi đáy,
d là trung đoạn.
b. Thể tích của hình chóp tứ giác đều
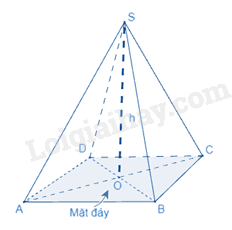
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng diện tích đáy nhân với chiều cao.
trong đó V là thể tích,
S là diện tích đáy,
h là chiều cao.
Ví dụ: Cho hình chóp tứ giác đều sau:
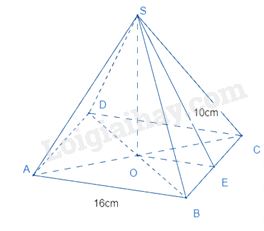
Diện tích xung quanh của hình chóp là:
Chiều cao của hình chóp là:
Thể tích của hình chóp là: