Với giải sách bài tập Toán 8 Bài 38: Hình chóp tứ giác đều sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán lớp 8 Bài 39: Hình chóp tứ giác đều
Bài 10.8 trang 76 SBT Toán lớp 8 Tập 2: Hãy cho biết đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, một trung đoạn của hình chóp tứ giác đều S.PQEF trong Hình 10.12.
Lời giải:
Đỉnh: S.
Các cạnh bên: SP, SQ, SE, SF.
Các mặt bên: SPQ, SQE, SEF, SPF.
Mặt đáy: PQEF.
Đường cao: SH.
Một trung đoạn: SA.
Bài 10.9 trang 76 SBT Toán lớp 8 Tập 2: Kẻ bảng sau vào vở và điền vào ô còn trống.
|
|
Đáy |
Mặt bên |
Số cạnh đáy |
Số cạnh bên |
Số mặt |
|
Hình chóp tam giác đều |
Tam giác đều |
|
|
|
|
|
Hình chóp tứ giác đều |
|
Tam giác cân |
|
|
|
Lời giải:
|
|
Đáy |
Mặt bên |
Số cạnh đáy |
Số cạnh bên |
Số mặt |
|
Hình chóp tam giác đều |
Tam giác đều |
Tam giác cân |
3 |
3 |
4 |
|
Hình chóp tứ giác đều |
Hình vuông |
Tam giác cân |
4 |
4 |
5 |
Bài 10.10 trang 76 SBT Toán lớp 8 Tập 2: Cho hình chóp tứ giác đều S.HKIJ có cạnh bên SI = 10 cm, cạnh đáy HK = 8 cm. Hãy cho biết:
a) Mặt bên và mặt đáy của hình chóp.
b) Độ dài các cạnh bên và các cạnh đáy còn lại của hình chóp.
Lời giải:
a) Các mặt bên của hình chóp: SHK, SHJ, SIJ, SKI.
Mặt đáy của hình chóp: HKIJ.
b) Các mặt bên của hình chóp tứ giác đều là các tam giác cân tại đỉnh nên các cạnh bên của hình chóp bằng nhau, do đó SK = SH = SJ = SI = 10 cm.
Mặt đáy của hình chóp tứ giác đều là hình vuông nên KI = IJ = HJ = HK = 8 cm.
Bài 10.11 trang 76 SBT Toán lớp 8 Tập 2: Cho hình chóp tứ giác đều D.ABCE có cạnh đáy bằng 6 cm, trung đoạn bằng 4 cm như Hình 10.13.
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Lời giải:
a) Diện tích xung quanh của hình chóp tứ giác đều là:
(cm2).
b) Diện tích mặt đáy là:
Sđ = 62 = 36 (cm2).
Bài 10.12 trang 77 SBT Toán lớp 8 Tập 2: Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều. Tính diện tích toàn phần của tứ giác đều tạo thành.
Lời giải:
Từ hình vẽ ta thấy hình chóp tứ giác đều được tạo thành cạnh đáy bằng 8 cm, trung đoạn bằng 9 cm.
Diện tích xung quanh của hình chóp tứ giác đều là:
(cm2).
Diện tích mặt đáy là: Sđ = 82 = 64 (cm2).
Diện tích toàn phần của hình chóp tứ giác đều là:
Stp = Sxq + Sđ = 144 + 64 = 208 (cm2).
Bài 10.13 trang 77 SBT Toán lớp 8 Tập 2: Bạn Thu dự định làm một chiếc đèn lồng có dạng là một hình chóp tứ giác đều cạnh đáy bằng 20 cm, chiều cao bằng 30 cm. Chiếc đèn lồng này có thể tích bằng bao nhiêu?
Lời giải:
Thể tích của chiếc đèn lồng là:
(cm3).
Bài 10.14 trang 77 SBT Toán lớp 8 Tập 2: Một hình chóp tứ giác đều có chiều cao bằng 12 cm, chu vi đáy bằng 32 cm. Thể tích của khối chóp này bằng bao nhiêu ?
Lời giải:
Mặt đáy của hình chóp tứ giác đều là hình vuông và có chu vi bằng 32 cm nên cạnh đáy của hình chóp tứ giác là: 32 : 4 = 8 (cm).
Thể tích của hình chóp là:
(cm3).
Diện tích toàn phần của hình chóp tứ giác đều là:
Stp = Sđ + Sxq = 36 + 48 = 84 (cm2).
Bài 10.15 trang 77 SBT Toán lớp 8 Tập 2: Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết .
Lời giải:
Hình chóp tứ giác đều có mặt bên là các tam giác cân tại đỉnh và mặt đáy là hình vuông.
Suy ra SC = SD = 5 cm; BC = CD = 5 cm.
Tam giác SBC cân tại đỉnh S có SI là đường cao, đồng thời là trung tuyến hay I là trung điểm của BC, do đó IB = IC = (cm).
Áp dụng định lý Pythagore vào tam giác SIC vuông tại I ta có:
SI2 + IC2 = SC2
Suy ra SI2 = SC2 – IC2 = 52 – (2,5)2 = 18,75.
Do đó, SI = cm.
Diện tích xung quanh của hình chóp là:
(cm2).
Xem thêm giải sách bài tập Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Hình chóp tứ giác đều
1. Định nghĩa
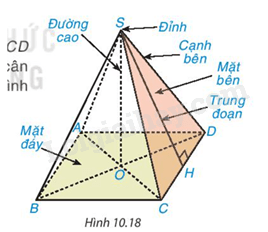
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của mặt đáy (giao điểm hai đường chéo)
2. Diện tích xung quanh và thể tích của hình chóp tứ giác đều
a. Diện tích xung quanh của hình chóp tứ giác đều
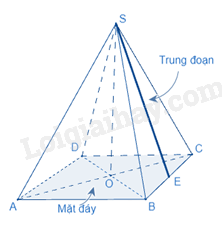
Diện tích xung quanh, kí hiệu là của hình chóp tứ giác đều được tính theo công thức:
,
trong đó p là nửa chu vi đáy,
d là trung đoạn.
b. Thể tích của hình chóp tứ giác đều
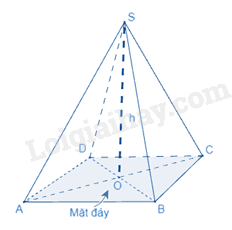
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng diện tích đáy nhân với chiều cao.
trong đó V là thể tích,
S là diện tích đáy,
h là chiều cao.
Ví dụ: Cho hình chóp tứ giác đều sau:
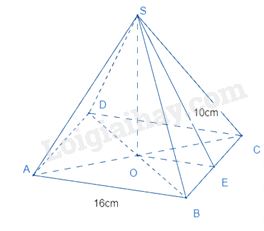
Diện tích xung quanh của hình chóp là:
Chiều cao của hình chóp là:
Thể tích của hình chóp là: