Với giải Bài 43 trang 104 SBT Toán lớp 11 Cánh diều chi tiết trong Bài 4: Hai mặt phẳng vuông góc giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 4: Hai mặt phẳng vuông góc
Bài 43 trang 104 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có ABCD là hình vuông, tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Chứng minh rằng:
a) (SAD) ⊥ (SAB);
b) (SBC) ⊥ (SAB);
c) (SAD) ⊥ (SBC).
Lời giải:
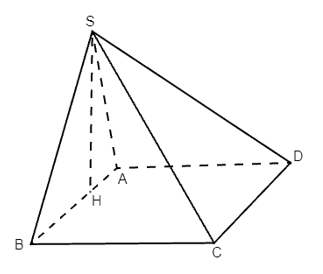
a) Gọi H là hình chiếu của S trên AB.
Ta có: (SAB) ⊥ (ABCD), (SAB) ∩ (ABCD) = AB và SH ⊂ (SAB), SH ⊥ AB
Suy ra SH ⊥ (ABCD).
Mà AD ⊂ (ABCD) nên SH ⊥ AD.
Do ABCD là hình vuông nên ta có AD ⊥ AB.
Ta có: AD ⊥ SH, AD ⊥ AB và SH ∩ AB = H trong (SAB)
Suy ra AD ⊥ (SAB).
Hơn nữa AD ⊂ (SAD) nên (SAD) ⊥ (SAB).
b) Vì SH ⊥ (ABCD) và BC ⊂ (ABCD) nên SH ⊥ BC.
Do ABCD là hình vuông nên ta có BC ⊥ AB.
Ta có: BC ⊥ SH, BC ⊥ AB và SH ∩ AB = H trong (SAB)
Suy ra BC ⊥ (SAB).
Hơn nữa BC ⊂ (SBC) nên (SBC) ⊥ (SAB).
c) Vì AD ⊥ (SAB) và SB ⊂ (SAB) nên AD ⊥ SB.
Theo giả thiết: tam giác SAB vuông tại S nên ta có SB ⊥ SA.
Ta có: SB ⊥ AD, SB ⊥ SA và AD ∩ SA = A trong (SAD)
Suy ra SB ⊥ (SAD).
Hơn nữa SB ⊂ (SBC) nên (SAD) ⊥ (SBC).
Xem thêm lời giải sách bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 35 trang 103 SBT Toán 11 Tập 2: Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì:...
Bài 38 trang 104 SBT Toán 11 Tập 2: Chứng minh các định lí sau:...
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
