Với giải sách bài tập Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
A.
B. 6a3;
C. 2a3;
D. a3.
Lời giải:
Đáp án đúng là: B
Thể tích của khối lăng trụ được tính theo công thức: V = Sh, trong đó S là diện tích đáy, h là chiều cao của khối lăng trụ.
Vậy thể tích của khối lăng trụ có S = 2a2 và h = 3a là: V = 2a2.3a = 6a3.
A.
B. 6a3;
C. 2a3;
D. a3.
Lời giải:
Đáp án đúng là: C
Thể tích của khối chóp được tính theo công thức: , trong đó S là diện tích đáy, h là chiều cao của khối chóp.
Vậy thể tích của khối chóp có S = 2a2 và h = 3a là:
A. 38a3;
B. 76a3;
C. 114a3;
D.
Lời giải:
Đáp án đúng là: A
Thể tích của khối chóp cụt đều được tính theo công thức: trong đó h là chiều cao và S1, S2 lần lượt là diện tích hai đáy của khối chóp cụt đều.
Vậy thể tích của khối chóp cụt đều có h = 6a, S1 = 4a2, S2 = 9a2 là:
Bài 54 trang 117 SBT Toán 11 Tập 2: Cho khối tứ diện đều ABCD cạnh a. Tính:
a) Khoảng cách giữa hai đường thẳng AB và CD;
b) Chiều cao và thể tích của khối tứ diện đều ABCD;
c) Côsin của góc giữa đường thẳng AB và mặt phẳng (BCD);
d) Côsin của số đo góc nhị diện [C, AB, D].
Lời giải:
a) Do ABCD là tứ diện đều cạnh nên các tam giác ABC, ABD, ACD, BCD là các tam giác đều cạnh a.
Gọi M, N lần lượt là trung điểm của AB và CD nên
Xét tam giác ABC đều có CM là đường trung tuyến (do M là trung điểm AB).
Suy ra CM là đường cao của tam giác ABC hay CM ⊥ AB.
Chứng minh tương tự đối với các tam giác ABD, BCD, ACD đều ta có: DM ⊥ AB, BN ⊥ CD, AN ⊥ CD.
· Ta có: AB ⊥ CM, AB ⊥ DM, CM ∩ DM = M trong (CDM)
Suy ra AB ⊥ (CDM).
Mà MN ⊂ (CDM) nên AB ⊥ MN.
· Ta có: CD ⊥ BN, CD ⊥ AN, BN ∩ AN = N trong (ABN)
Suy ra CD ⊥ (ABN).
Mà MN ⊂ (ABN) nên CD ⊥ MN.
Ta có: AB ⊥ MN, CD ⊥ MN.
Suy ra MN là đoạn vuông góc chung của hai đường thẳng AB và CD.
Như vậy: d(AB, CD) = MN.
Áp dụng định lí Pythagore trong tam giác BCM vuông tại M có:
MC2 = BC2 – BM2
Áp dụng định lí Pythagore trong tam giác CMN vuông tại N có:
CM2 = MN2 + CN2
Vậy
b) Gọi H là hình chiếu của A trên (BCD) hay AH ⊥ (BCD).
Do ABCD là tứ diện đều, nên H là tâm đường tròn ngoại tiếp của tam giác BCD.
Vì tam giác BCD đều nên H cũng là trọng tâm của tam giác BCD.
Mà BN là đường trung tuyến của tam giác BCD (do N là trung điểm của CD)
Suy ra: H ∈ BN và
Ta có: AH ⊥ (BCD), BH ⊂ (BCD) nên AH ⊥ BH.
Áp dụng định lí Pythagore trong tam giác BCN vuông tại N có:
BC2 = BN2 + CN2
Suy ra
Từ đó ta có
· Áp dụng định lí Pythagore trong tam giác ABH vuông tại H (do AH ⊥ BH) có:
AB2 = AH2 + BH2
Suy ra
· Diện tích tam giác BCD là:
(đvdt).
· Thể tích của khối tứ diện ABCD có đường cao và diện tích đáy là:
(đvtt).
c) Do H là hình chiếu của A trên (BCD) nên góc giữa đường thẳng AB và mặt phẳng (BCD) bằng góc giữa hai đường thẳng AB và BH và bằng
Xét tam giác ABH vuông tại H có:
Vậy côsin của góc giữa đường thẳng AB và mặt phẳng (BCD) là
d) Theo câu a ta có: CM ⊥ AB, DM ⊥ AB, CM ∩ DM = M ∈ AB.
Nên là góc phẳng nhị diện của góc nhị diện [C, AB, D].
Xét tam giác CMD, theo hệ quả định lí Côsin ta có:
Vậy côsin của số đo góc nhị diện [C, AB, D] bằng
Bài 55 trang 117 SBT Toán 11 Tập 2: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính:
a) Khoảng cách giữa hai mặt phẳng (ABCD) và (A’B’C’D’);
b) Số đo của góc nhị diện [A, CD, B’];
c) Tang của góc giữa đường thẳng BD’ và mặt phẳng (ABCD);
d) Khoảng cách giữa hai đường thẳng C’D và BC;
e*) Góc giữa hai đường thẳng BC’ và CD’.
Lời giải:
Ta có: ABCD.A’B’C’D’ là hình lập phương cạnh a nên tất cả các mặt bên và hai mặt đáy của hình lập phương ABCD. A’B’C’D’ đều là hình vuông cạnh a.
a) Do ABCD.A’B’C’D’ là hình lập phương nên ta có (ABCD) // (A’B’C’D’) và AA’ ⊥ (ABCD).
Như vậy: d((ABCD), (A’B’C’D’)) = d(A’, (ABCD)) = AA’ = a.
b) Do ABCD.A’B’C’D’ là hình lập phương nên ta có A’B’ // DC.
Suy ra bốn điểm A’, B’, C, D đồng phẳng.
Khi đó, góc nhị diện [A, CD, B’] bằng góc nhị diện [A, CD, A’].
Ta có: CD ⊥ AD, CD ⊥ DD’ (do ABCD, D’C’CD là hai hình vuông), AD ∩ DD’ = D trong (A’D’DA).
Suy ra CD ⊥ (A’D’DA).
Hơn nữa A’D ⊂ (A’D’DA).
Nên ta có CD ⊥ A’D.
Ta thấy: A’D ⊥ CD, AD ⊥ CD (do ABCD là hình vuông), AD ∩ A’D = D ∈ CD.
Suy ra là góc phẳng nhị diện của góc nhị diện [A, CD, A’] hay góc nhị diện [A, CD, B’].
Vì ADD’A là hình vuông nên
Vậy số đo của góc nhị diện [A, CD, B’] bằng 45°
c) Vì DD’ ⊥ (ABCD) nên góc giữa đường thẳng BD’ và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng BD’ và BD và bằng
Do ABCD là hình vuông cạnh a, nên ta có
Ta có: DD’ ⊥ (ABCD), BD ⊂ (ABCD) nên DD’ ⊥ BD.
Xét tam giác D’DB vuông tại D có:
Vậy tang của góc giữa đường thẳng BD’ và mặt phẳng (ABCD) bằng
d) Gọi I là giao điểm của CD’ và C’D.
Do D’C’CD là hình vuông nên I là trung điểm của CD’ và CD’ ⊥ C’D hay IC ⊥ C’D.
Ta có: BC ⊥ (D’C’CD) (do ABCD.A’B’C’D’ là hình lập phương)
Mà IC ⊂ (D’C’CD) nên BC ⊥ IC.
Ta thấy: IC ⊥ C’D, IC ⊥ BC nên IC là đoạn vuông góc chung của hai đường thẳng C’D và BC.
Như vậy:
Do ABCD, D’C’CD, A’D’DA là các hình vuông cạnh a nên có các đường chéo
Suy ra
Vậy khoảng cách giữa hai đường thẳng C’D và BC bằng
e*) Ta có: D’C’ song song và bằng DC, DC song song và bằng AB (do DC’CD, ABCD là hai hình vuông cạnh a), nên D’C’ song song và bằng AB.
Suy ra ABC’D’ là hình bình hành nên ta có BC’ // AD’.
Khi đó góc giữa hai đường thẳng BC’ và CD’ bằng góc giữa hai đường thẳng AD’ và CD’ và bằng
Vì nên tam giác ACD’ là tam giác đều.
Suy ra
Vậy góc giữa hai đường thẳng BC’ và CD’ bằng 60°.
Lời giải:
Ta thấy rằng đáy của viên gạch cần làm là lục giác đều.
Chia hình lục giác đều thành 6 hình tam giác đều có cạnh là 21,5 cm (hình vẽ trên).
Gọi ABC là tam đều cạnh 21,5 cm, kẻ đường cao AH (H ∈ BC) (hình vẽ trên).
Suy ra AH cũng là đường trung tuyến của tam giác ABC hay H là trung điểm của BC.
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có:
AC2 = AH2 + HC2
Suy ra
Từ đó ta có diện tích tam giác ABC đều cạnh 21,5 cm là
Như vậy, ta có diện tích 1 tam giác đều cạnh 21,5 cm là:
Khi đó, diện tích đáy của viên gạch (gồm 6 hình tam giác đều có cạnh là 21,5 cm) là: (cm2).
Vậy thể tích bê tông cần dùng để làm một viên gạch có dạng khối lăng trụ với chiều cao h = 4 cm và diện tích đáy (cm2) là:
(cm3).
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 4: Hai mặt phẳng vuông góc
Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
Lý thuyết Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
1. Hình lăng trụ đứng. Hình lăng trụ đều
- Hình lăng trụ có cạnh bên vuông góc với mặt đáy được gọi là hình lăng trụ đứng.
- Hình lăng trụ đứng có đáy là đa giác đều gọi là hình lăng trụ đều.
- Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.
Ví dụ: Hình dưới biểu diễn hình lăng trụ đứng tứ giác ABCD.A'B'C'D'.
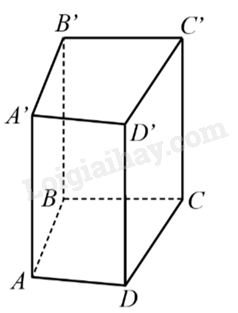
Nhận xét:
- Mỗi mặt bên của hình lăng trụ đứng là một hình chữ nhật, mặt phẳng chứa nó vuông góc với mặt đáy.
- Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
Hình hộp chữ nhật có 6 mặt là hình chữ nhật.
Nếu mỗi mặt của hình hộp là hình chữ nhật thì hình hộp đó là hình hộp chữ nhật.
Độ dài các đường chéo của hình hộp chữ nhật là bằng nhau.
- Hình lập phương là hình hộp chữ nhật có tất cả các mặt là hình vuông.
Hình lập phương là hình lăng trụ tứ giác đều có cạnh bên bằng cạnh đáy.
2. Hình chóp đều. Hình chóp cụt đều
a) Hình chóp đều
Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
Chú ý:
- Hình chóp tam giác đều có cạnh bên bằng cạnh đáy là tứ diện đều.
- Đoạn thẳng nối đỉnh với hình chiếu của đỉnh trên mặt đáy gọi là đường cao.
Ví dụ: Hình dưới đây biểu diễn hình chóp tứ giác đều S.ABCD.
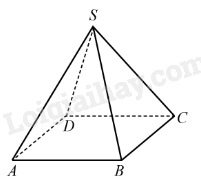
Nhận xét: Chân đường cao của hình chóp đều là tâm đường tròn ngoại tiếp của đáy.
b) Hình chóp cụt đều
Cho hình chóp đều . Mặt phẳng song song với đáy của hình chóp và cắt các cạnh lần lượt tại .
Phần của hình chóp đã cho giới hạn bởi hai mặt phẳng và được gọi là hình chóp cụt đều .
Trong hình chóp cụt đều , ta gọi:
- Các đa giác lần lượt là đáy lớn, đáy nhỏ;
- Các tứ giác là các mặt bên;
- Các đoạn thẳng là các cạnh bên;
- Các cạnh của hai đa giác là các cạnh đáy.
Ví dụ: Hình dưới đây biểu diễn hình chóp cụt tứ giác đều .
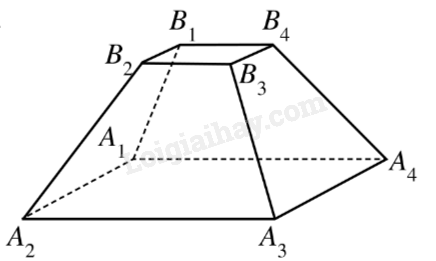
Nhận xét:
- Hai đáy của hình chóp cụt đều nằm trên hai mặt phẳng song song và có các cạnh tương ứng song song; dồng thời hai dáy dó là các da giác dều có củng số cạnh;
- Mỗi mặt bên cùa hình chóp cụt đều là một hình thang cân;
- Các đường thẳng chứa cạnh bên của hình chóp cụt đều cùng đi qua một điểm;
- Đoạn thẳng nối tâm của hai đáy vuông góc với hai đáy của hình chóp cụt đều và gọi là đường cao.
3. Thể tích của một số hình khối
Phần không gian được giới hạn bởi một hình lăng trụ (kể cả hình lăng trụ ấy) được gọi là khối lăng trụ. Các khối khác được định nghĩa tương tự.
a) Thể tích của khối lăng trụ
- Chiều cao của khối lăng trụ bằng khoảng cách giữa hai mặt đáy.
- Thể tích của khối lăng trụ được tính theo công thức:
trong đó là chiều cao, là diện tích đáy của khối lăng trụ.
b) Thể tích của khối chóp
- Chiều cao của khối chóp bằng khoảng cách từ đỉnh đến mặt đáy.
- Thể tích của khối chóp được tính theo công thức:
trong đó là chiều cao, là diện tích đáy của khối chóp.
c) Thể tích của khối chóp cụt đều
- Chiều cao của khối chóp cụt đều bằng khoảng cách giữa hai mặt đáy.
- Thể tích của khối chóp cụt đều được tính theo công thức:
trong đó là chiều cao và lần lượt là diện tích hai đáy của khối chóp cụt đều.