Với lời giải SBT Toán 8 trang 19 Tập 2 Bài tập cuối chương 5 trang 18 sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 5 trang 18

Bài 8 trang 19 SBT Toán 8 Tập 2: Đoạn thẳng trong hình vẽ bên là tập hợp những điểm (x; y) thoả mãn điều kiện nào dưới đây?

A. –1 $\le$ y $\le$ 3 và x = 2.

B. –1 £ x $\le$ 3 và y $\le$ 2.

C. –1 $\le$ x $\le$ 3 và y = 2.

D. x ≥ –1 và y = 2.

Lời giải:

Đáp án đúng là: C

Dựa vào hình vẽ ta thấy đoạn thẳng đi qua các điểm có tung độ y = 2 và có hoành độ nằm trong đoạn [–1; 3].

Bài 9 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = 5x + 10. Giá trị của hàm số tại x = a – 1 là:

A. 5a + 5.

B. 5a + 15.

C. 5a + 3.

D. 5a – 5.

Lời giải:

Đáp án đúng là: A

Thay x = a – 1 vào hàm số y = 5x + 10, ta được:

y = 5(a – 1) + 10 = 5a – 5 + 10 = 5a + 5.

Bài tập tự luận

Bài 10 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = 3x – 2. Tính f(–5); f(–4); f(0); f(1); f(2); f(a); f(a + 1).

Lời giải:

Ta có: y = f(x) = 3x – 2.

•Thay x = –5 vào f(x) ta được: f(–5) = 3.(–5) – 2 = –17.

•Thay x = –4 vào f(x) ta được: f(–4) = 3.(–4) – 2 = –14.

•Thay x = 0 vào f(x) ta được: f(0) = 3.0– 2 = –2.

•Thay x = 1 vào f(x) ta được: f(1) = 3.1 – 2 = 1.

•Thay x = 2 vào f(x) ta được: f(2) = 3.2 – 2 = 4.

•Thay x = a vào f(x) ta được: f(a) = 3a – 2.

•Thay x = a + 1 vào f(x) ta được: f(a + 1) = 3(a + 1) – 2 = 3a + 1.

Vậy f(–5) = –17; f(–4) = –14; f(0) = –2; f(1) = 1; f(2) = 4; f(a) = 3a – 2; f(a + 1) = 3a + 1.

Bài 11 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = $\frac{2}{3}$x + 5. Tìm toạ độ giao điểm của đồ thị hàm số đã cho với trục Ox và trục Oy.

Lời giải:

•Đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5cắt Ox tại M nên y_M = 0.

Do đó: $\frac{2}{3}$x + 5 = 0 $\iff$$\frac{2}{3}$x = -5 $\iff$ x = $\frac{-15}{2}$.

Suy ra đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5 cắt Ox tại $M\left(\frac{-15}{2};0\right)$.

•Đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5 cắt Oy tại N nên x_N = 0.

Thay x_N = 0 vào f(x) ta có: y = $\frac{2}{3}$.0 + 5 = 5.

Suy ra đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5 cắt Oy tại N(0; 5).

Vậy đồ thị hàm số y = f(x) $\frac{2}{3}$x + 5 cắt Ox, Oy tại $M\left(\frac{-15}{2};0\right)$ và N(0; 5).

Bài 12 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = (m + 1)x + 5.

a) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.

b) Với giá trị nào của m thì đồ thị hàm số đã cho đi qua điểm A(5; 0)?

Lời giải:

a) Để y = f(x) = (m + 1)x + 5 là hàm số bậc nhất thì m + 1 $\ne$ 0 hay m $\ne$ –1.

Vậy điều kiện của m để hàm số đã cho là hàm số bậc nhất là m $\ne$ –1.

b) Vì đồ thị hàm số đã cho đi qua điểm A(5; 0) nên ta có:

0 = 5(m + 1) + 5

$\iff$ 5m + 10 = 0

$\iff$ m = –2

Vậy m = –2.

Bài 13 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = (m – 3)x.

a) Với giá trị nào của m thì đồ thị hàm số đã cho đi qua điểm A(1; 2)?

b) Với giá trị nào của m thì đồ thị hàm số đã cho đi qua điểm B(1; –2)?

Lời giải:

a) Vì đồ thị hàm số đã cho đi qua điểm A(1; 2) nên ta có:

2 = 1(m – 3)

$\iff$ m – 3 = 2

$\iff$ m = 5

Vậy m = 5.

b) Vì đồ thị hàm số đã cho đi qua điểm B(1; –2) nên ta có:

–2 = 1.(m – 3)

$\iff$ m – 3 = –2

$\iff$ m = 1

Vậy m = 1.

Bài 14 trang 19 SBT Toán 8 Tập 2: Cho hai d: y = x – 2 và d’: y = –2x + 1.

a) Tìm hệ số góc của hai đường thẳng d và d’.

b) Tìm toạ độ giao điểm của hai đường thẳng d và d’ với trục Ox và Oy.

c) Với giá trị nào của m thì đồ thị hàm số y = (m – 2)x – m song song với d và cắt d’.

Lời giải:

a) Đường thẳng d: y = x – 2 có hệ số góc là a = 1.

Đường thẳng d’: y = –2x + 1 có hệ số góc là a = –2.

b) +) Xét hàm số y = x – 2

Đồ thị hàm số y = x – 2 cắt Ox tại M nên y_M = 0.

Do đó: x – 2 = 0 $\iff$ x = 2.

Suy ra đồ thị hàm số y = x – 2 cắt Ox tại M(2; 0).

Đồ thị hàm số y = x – 2 cắt Oy tại N nên x_N = 0.

Thay x_N = 0 vào f(x) ta có: y = 0 – 2 = –2.

Suy ra đồ thị hàm số y = x – 2 cắt Oy tại N(0; –2).

+) Xét hàm số y = –2x + 1.

Đồ thị hàm số y = –2x + 1 cắt Ox tại P nên y_P = 0.

Do đó: -2x + 1 = 0 $\iff$ x = $\frac{1}{2}$

Suy ra đồ thị hàm số y = –2x + 1 cắt Ox tại $P\left(\frac{1}{2};0\right)$.

Đồ thị hàm số y = –2x + 1 cắt Oy tại Q nên x_Q = 0.

Thay x_Q = 0 vào f(x) ta có: y = –2.0 + 1 = 1.

Suy ra đồ thị hàm số y = –2x + 1 cắt Oy tại Q(0; 1).

Vậy đồ thị hàm số y = x – 2 cắt Ox, Oy tại M(2; 0) và N(0; –2).

Đồ thị hàm số y = –2x + 1 cắt Ox, Oy tại $P\left(\frac{1}{2};0\right)$ và Q(0; 1).

c) Đồ thị hàm số y = (m – 2)x – m cắt d’: y = –2x + 1 nên m – 2 $\ne$ –2 $\iff$ m $\ne$ 0.

Đồ thị hàm số y = (m – 2)x – m song song với d: y = x – 2 thì

Vậy m = 3 thoả mãn đề bài.

Bài 15 trang 19 SBT Toán 8 Tập 2: Cho đường thẳng d: y = (m – 2)x + 1. Với giá trị nào của m để:

a) Đường thẳng d song song với đường thẳng d₁: y = 2x + 3.

b) Đường thẳng d cắt đường thẳng d₂: y = –5x + 1.

Lời giải:

a) Đường thẳng y = (m – 2)x + 1 song song với đường thẳng y = 2x + 3.

Suy ra m – 2 = 2 $\iff$ m = 4.

Vậy m = 4.

b) Đường thẳng y = (m – 2)x + 1 cắt đường thẳng y = –5x + 1.

Suy ra m – 2 $\ne$ –5 $\iff$ m $\ne$ –3.

Vậy m $\ne$ –3.

Bài 16 trang 19 SBT Toán 8 Tập 2: Xác định hàm số y = ax + b biết đồ thị của hàm số đã cho song song với đường thẳng y = –2x + 3 và đi qua A(1; –3).

Lời giải:

Đồ thị của hàm số y = ax + b song song với đường thẳng y = –2x + 3 nên a = –2 và b $\ne$ 3.

Ta được hàm số y = –2x + b.

Đồ thị của hàm số y = –2x + b đi qua A(1; –3) nên ta có:

–3 = –2.1 + b $\iff$ b = –1.

Vậy hàm số cần tìm có phương trình y = –2x – 1.

Bài 17 trang 19 SBT Toán 8 Tập 2: Tìm điểm cố định mà mỗi đường thẳng d’: y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Lời giải:

Giả sử điểm cố định của đồ thị hàm số y = (m – 2)x + 3 là I(x₀; y₀).

Thay x = x₀ và y = y₀ vào y = (m – 2)x + 3, ta được:

y₀ = (m – 2)x₀ + 3

$\iff$ mx₀ – 2x₀ + 3 – y₀ = 0

$\iff$ mx₀ – (y₀ + 2x₀ – 3) = 0 (1)

Để (1) luôn đúng với mọi giá trị của m thì .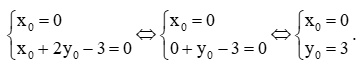

Vậy đồ thị hàm số y = (m – 2)x + 3 luôn đi qua điểm cố định I(0; 3).