Với lời giải SBT Toán 8 trang 55 Tập 1 Bài tập cuối chương 4 sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 4

Bài 4.15 trang 55 sách bài tập Toán 8 Tập 1: Cho tam giác ABC, điểm I nằm trong tam giác. Lấy điểm D trên IA, qua D kẻ đường thẳng song song với AB, cắt IB tại E. Qua E kẻ đường thẳng song song với BC, cắt IC tại F. Chứng minh rằng: DF // AC.

Lời giải:

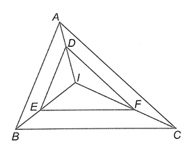
Trong ∆AID có DE // AB suy ra $\frac{ID}{IA}=\frac{IE}{IB}$(định lí Thalès)

Trong ∆IBC có EF // BC suy ra $\frac{IE}{IB}=\frac{IF}{IC}$(định lí Thalès).

Suy ra $\frac{ID}{IA}=\frac{IF}{IC}$

Trong ∆AIC có $\frac{ID}{IA}=\frac{IF}{IC}$ nên DF // AC (định lí Thalès đảo).

Bài 4.16 trang 55 sách bài tập Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh MI = IK = KN.

Lời giải:

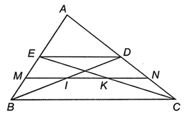
Trong ∆ABC có các đường trung tuyến BD, CE nên D là trung điểm của AC, E là trung điểm của AB nên ED là đường trung bình của ∆ABC

Suy ra $ED=\frac{1}{2}BC$ và ED // BC (tính chất đường trung bình của tam giác)

Ta có: E là trung điểm của AB nên $AE=EB=\frac{1}{2}AB$

Mà M là trung điểm của EB nên $EM=MB=\frac{1}{2}EB=\frac{1}{4}AB$ hay $\frac{MB}{AB}=\frac{1}{4}$

Tương tự, ta cũng có $NC=\frac{1}{4}AC$ hay $\frac{NC}{AC}=\frac{1}{4}$

Suy ra $\frac{MB}{AB}=\frac{NC}{AC}\left(=\frac{1}{4}\right)$

Xét DABC có $\frac{MB}{AB}=\frac{NC}{AC}$ nên MN // BC (định lí Thalès đảo)

Lại có ED // BC nên ED // MN // BC.

Xét DBDE có M là trung điểm của EB và MI // ED (do ED // MN)

Suy ra I là trung điểm của BD hay IB = ID

Khi đó MI là đường trung bình của DBDE nên $MI=\frac{1}{2}ED$.

Tương tự, trong DCDE ta cũng có $KN=\frac{1}{2}ED,$ trong DBCE có $MK=\frac{1}{2}BC$.

Ta có $IK=MK-MI=\frac{1}{2}BC-\frac{1}{2}ED=ED-\frac{1}{2}ED=\frac{1}{2}ED$.

Do đó $MI=IK=KN=\frac{1}{2}ED$.

Bài 4.17 trang 55 sách bài tập Toán 8 Tập 1: Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh DE // BC.

Lời giải:

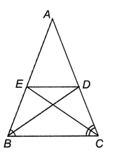
Trong ∆ABC có BD là phân giác của $\widehat{ABC}$ nên $\frac{DA}{DC}=\frac{BA}{BC}$ (tính chất đường phân giác của tam giác). (1)

Trong ∆ABC có CE là phân giác của $\widehat{ACB}$ nên $\frac{EA}{EB}=\frac{CA}{CB}$(tính chất đường phân giác trong tam giác). (2)

Mà ∆ABC cân tại A nên AB = AC  (3)

Từ (1), (2), (3), suy ra: $\frac{DA}{DC}=\frac{EA}{EB}$.

Xét DABC có $\frac{DA}{DC}=\frac{EA}{EB}$, suy ra ED // BC (định lí Thales đảo).

Bài 4.18 trang 55 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD, điểm E thuộc cạnh AB (E khác A và B), điểm F thuộc cạnh AD (F khác A và D). Đường thẳng qua D song song với EF cắt AC tại I. Đường thẳng qua B song song với EF cắt AC tại K.

a) Chứng minh rằng: AI = CK.

b) Gọi N là giao điểm của EF và AC. Chứng minh rằng: $\frac{AB}{AE}+\frac{AD}{AF}=\frac{AC}{AN}$.

Lời giải:

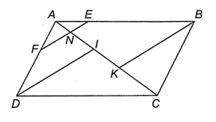
a) Ta có DI // EF và BK // EF nên EF // DI // BK

Do DI // BK nên $\widehat{CID}=\widehat{AKB}$(hai góc so le trong)

Mà $\widehat{AID}+\widehat{CID}=180°;\widehat{CKB}+\widehat{AKB}=180°$

Suy ra $\widehat{AID}=\widehat{CKB}$(1)

Do ABCD là hình bình hành nên AD = BC và AD // BC

Suy ra $\widehat{DAC}=\widehat{BCA}$(so le trong) hay $\widehat{DAI}=\widehat{BCK}$(2)

Xét DADI có $\widehat{AID}+\widehat{DAI}+\widehat{ADI}=180°$(3)

Xét DCBK có $\widehat{CKB}+\widehat{BCK}+\widehat{CBK}=180°$(4)

Từ (1), (2), (3) và (4) suy ra $\widehat{ADI}=\widehat{CBK}$

Xét DADI và DCBK có:

(cmt); AD = BC (cmt); (cmt)

Do đó DADI = DCBK (g.c.g)

Suy ra AI = CK (hai cạnh tương ứng).

b) Trong ∆ABK có NE // BK nên $\frac{AB}{AE}=\frac{AK}{AN}$(định lí Thalès).

Trong ∆ADI có FN // DI nên $\frac{AD}{AF}=\frac{AI}{AN}$(định lí Thalès),

Mà AI = CK (câu a) nên $\frac{AD}{AF}=\frac{CK}{AN}$

Suy ra $\frac{AB}{AE}+\frac{AD}{AF}=\frac{AK}{AN}+\frac{CK}{AN}=\frac{AK+CK}{AN}=\frac{AC}{AN}$

Bài 4.19 trang 55 sách bài tập Toán 8 Tập 1: Cho góc xOy nhọn. Trên cạnh Ox lấy điểm N, trên cạnh Oy lấy điểm M. Gọi I là một điểm trên đoạn thẳng MN. Qua I kẻ đường thẳng song song với Ox cắt Oy tại A (A khác M và N) và đường thẳng song song với Oy cắt Ox ở B. Chứng minh rằng: $\frac{MA}{MO}+\frac{NB}{NO}=1.$

Lời giải:

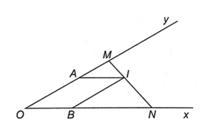
Xét ∆OMN có AI // ON nên $\frac{MA}{MO}=\frac{MI}{MN}$(định lí Thalès);

Và IB // MO nên $\frac{NB}{NO}=\frac{NI}{NM}$(định lí Thalès).

Suy ra $\frac{MA}{MO}+\frac{NB}{NO}=\frac{MI}{MN}+\frac{NI}{NM}=\frac{MI+NI}{MN}=\frac{MN}{MN}=1$.

Bài 4.20 trang 55 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD, AC cắt BD tại O. Đường phân giác góc A cắt BD tại M, đường phân giác D cắt AC tại N. Chứng minh MN // AD.

Lời giải:

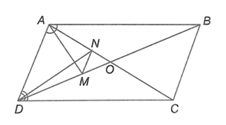
Trong ∆ABD có: AM là phân giác của góc $\widehat{BAD}$ nên $\frac{AB}{AD}=\frac{MB}{MD}$(tính chất đường phân giác trong tam giác)

Tương tự: trong ∆ADC có DN là phân giác góc $\widehat{ADC}$ nên $\frac{DC}{DA}=\frac{NC}{NA}$

Mà AB = DC (do ABCD là hình bình hành) suy ra $\frac{MB}{MD}=\frac{NC}{NA}$.

Từ đó, ta có: $\frac{MB}{MD}+1=\frac{NC}{NA}+1$ hay $\frac{MB+MD}{MD}=\frac{NC+NA}{NA}$ 

Suy ra $\frac{BD}{MD}=\frac{AC}{NA}$(1)

Mà ABCD là hình bình hành nên 2 đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường, suy ra BD = 2DO, AC = 2AO (2)

Từ (1) và (2) suy ra $\frac{2DO}{DM}=\frac{2AO}{AN}$ hay $\frac{DO}{DM}=\frac{AO}{AN}$

Xét DOAD có $\frac{DO}{DM}=\frac{AO}{AN}$ nên MN // AD (định lí Thalès đảo).