Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng chi tiết sách Toán 11 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Giải Toán 11 trang 38 Tập 2

Mở đầu trang 38 Toán 11 Tập 2: Vào khoảng thời gian giữa mùa hè, ở phía bắc của vòng Bắc Cực (như một số vùng phía bắc của Na Uy, Phần Lan, Nga,...), Mặt Trời có thể được nhìn thấy trong suốt 24 giờ của ngày. Hình học giải thích hiện tượng này như thế nào?

Lời giải:

Trong cả ngày 22 tháng 6 của năm, hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo (P) gần như chính là đường thẳng ∆ nối giữa tâm Trái Đất, tâm Mặt Trời và cực Bắc của Trái Đất nghiêng về phía Mặt Trời (hình dưới). Do đó, góc giữa trục Trái Đất và đường nối hai tâm xấp xỉ bằng 66,5°. Mặt khác, Mặt Trời chiếu sáng nửa Trái Đất được cắt bởi mặt phẳng vuông góc với ∆. Vì vậy, trong cả ngày 22 tháng 6, mặc dù Trái Đất quay quanh trục và di chuyển trên quỹ đạo, nhưng gần như toàn bộ vùng có vĩ độ Bắc lớn hơn 66,5° (phía bắc vòng Bắc Cực) luôn được Mặt Trời chiếu sáng.

1. Phép chiếu vuông góc

HĐ1 trang 38 Toán 11 Tập 2: Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.

a) Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua một phép chiếu song song hay không?

b) Khi tia sáng mặt trời vuông góc với mặt sân, liệu ta có thể quan sát được bóng của cây cột trên sân hay không?

Lời giải:

a) Bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua một phép chiếu song song theo phương tia sáng mặt trời lên mặt sân.

b) Khi tia sáng mặt trời vuông góc với mặt sân thì hình chiếu của cột thu về chân cột nên ta không thể quan sát được bóng của cây cột trên sân.

Giải Toán 11 trang 39 Tập 2

Câu hỏi trang 39 Toán 11 Tập 2: a) Nếu A là một điểm không thuộc mặt phẳng (P) và A' là hình chiếu của A trên (P) thì đường thẳng AA' có quan hệ gì với mặt phẳng (P)?

b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là gì?

Lời giải:

a) Nếu A là một điểm không thuộc mặt phẳng (P) và A' là hình chiếu của A trên (P) thì đường thẳng AA' vuông góc với mặt phẳng (P).

b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là một điểm chính là giao điểm của a và (P).

HĐ2 trang 39 Toán 11 Tập 2: Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Xét b là một đường thẳng nằm trong (P). Trên a, lấy hai điểm M, N tùy ý. Gọi M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) (H.7.34).

a) Hình chiếu của a trên mặt phẳng (P) là đường thẳng nào?

b) Nếu b vuông góc với M'N' thì b có vuông góc với a hay không?

c) Nếu b vuông góc với a thì b có vuông góc với M'N' hay không?

Lời giải:

a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là đường thẳng a' đi qua hai điểm M', N'.

b) Do M' là hình chiếu của M trên mặt phẳng (P) nên M'M ⊥ (P), mà b thuộc (P) nên M'M ⊥ b.

Vì b ⊥ M'N' và b ⊥ M'M nên b ⊥ mp(M'N', M'M).

Mà a thuộc mp(M'N', M'M) nên b ⊥ a.

c) Do M' là hình chiếu của M trên mặt phẳng (P) nên M'M ⊥ (P), mà b thuộc (P) nên M'M ⊥ b.

Vì b ⊥ a và b ⊥ M'M nên b ⊥ mp(a, M'M).

Mà M'N' thuộc mp(a, M'M) nên b ⊥ M'N'.

Giải Toán 11 trang 40 Tập 2

Luyện tập 1 trang 40 Toán 11 Tập 2: Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).

a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.

b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).

c) Chứng minh rằng nếu $AO\perp BC$ thì $SA\perp BC$.

d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC).

Lời giải:

a) Vì O là hình chiếu của S trên mặt phẳng (ABC) nên SO ⊥ (ABC), suy ra SO ⊥ OA, SO ⊥ OB, SO ⊥ OC.

Xét tam giác SOA vuông tại O, có SO² + OA² = SA².

Xét tam giác SOB vuông tại O, có SO² + OB² = SB².

Xét tam giác SOC vuông tại O, có SO² + OC² = SC².

Mà SA = SB = SC nên OA = OB = OC hay O là tâm đường tròn ngoại tiếp tam giác ABC.

b) O là hình chiếu của S trên mặt phẳng (ABC), A là hình chiếu của A trên mặt phẳng (ABC). Do đó OA là hình chiếu của SA trên mặt phẳng (ABC).

c) Vì SO ⊥ (ABC) nên SO ⊥ BC mà AO ⊥ BC nên BC ⊥ (SAO), suy ra BC ⊥ SA.

d) O là hình chiếu của S trên mặt phẳng (ABC).

A là hình chiếu của A trên mặt phẳng (ABC).

B là hình chiếu của B trên mặt phẳng (ABC).

C là hình chiếu của C trên mặt phẳng (ABC).

Do đó hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC) lần lượt là: OBC, OCA, OAB.

HĐ3 trang 40 Toán 11 Tập 2: Một máy bay giữ vận tốc không đổi, với độ lớn 240 km/h trong suốt 2 phút đầu kể từ khi cất cánh. Hỏi thông tin trên có đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh không?

Lời giải:

Thông tin trên chưa đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh.

Giải Toán 11 trang 42 Tập 2

Vận dụng trang 42 Toán 11 Tập 2: Tâm Trái Đất chuyển động quanh Mặt Trời theo quỹ đạo là một đường elip nhận tâm Mặt Trời làm tiêu điểm. Trong quá trình chuyển động, Trái Đất lại quay quanh trục Bắc Nam. Trục này có phương không đổi và luôn tạo với mặt phẳng chứa quỹ đạo một góc khoảng 66,5°.

(Theo nationalgeographic.org).

a) Giải thích vì sao hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo (P) cũng có phương không đổi.

b) Giải thích vì sao có hai thời điểm trong năm mà tại đó hình chiếu của trục Trái Đất trên mặt phẳng (P) thuộc đường thẳng nối tâm Mặt Trời và tâm Trái Đất.

Lời giải:

a)

Gọi a, b là hai vị trí của trục Trái Đất, a // b.

Gọi a', b' tương ứng là hình chiếu của a, b trên (P).

Hai mặt phẳng mp(a, a') và mp(b, b') chứa hai phương tương ứng song song với nhau đó là các phương cùng vuông góc với (P) và a // b. Do đó hai mặt phẳng mp(a, a') và mp(b, b') song song với nhau hoặc trùng nhau. Suy ra giao tuyến của chúng với (P) là a' và b' cũng song song hoặc trùng nhau.

b) Hình chiếu của trục Trái Đất lên mặt phẳng (P) có phương cố định. Gọi m là đường thẳng đi qua tâm Mặt Trời và có phương cố định nói trên. Khi đó, hình chiếu của trục Trái Đất xuống (P) thuộc đường thẳng m khi và chỉ khi tâm Trái Đất ở vị trí là giao của m với đường elip quỹ đạo của Trái Đất. Như vậy có hai vị trí thuộc quỹ đạo, ứng với hai thời điểm trong năm mà hình chiếu của trục Trái Đất trên (P) thuộc đường thẳng m (nối tâm Mặt Trời và tâm Trái Đất).

Khám phá trang 42 Toán 11 Tập 2: Cho đường thẳng ∆ vuông góc với mặt phẳng (P). Khi đó, với một đường thẳng a bất kì, góc giữa a và (P) có mối quan hệ gì với góc giữa a và ∆?

Lời giải:

Ta xét 3 trường hợp sau:

Trường hợp 1: a ⊥ (P).

Vì a ⊥ (P) và ∆ ⊥ (P) nên a // ∆. Khi đó (a, ∆) = 0°; (a, P) = 90°.

Trường hợp 2: a // (P) hoặc a thuộc (P).

Vì a // (P) hoặc a thuộc (P) và ∆ ⊥ (P) nên a ⊥ ∆. Khi đó (a, ∆) = 90°; (a, P) = 0°.

Trường hợp 3: a không vuông góc với (P) và a cắt (P) tại O.

Lấy điểm A khác O thuộc a và gọi H là hình chiếu vuông góc của A trên (P).

Có AH ⊥ (P) và ∆ ⊥ (P) nên AH // ∆.

Khi đó (∆, a) = (AH, a) = $\widehat{HAO}$ $=90°-\widehat{HOA}$ $=90°-(a,P)$.

Vậy góc giữa a và ∆ phụ thuộc vào góc giữa a và (P).

Trải nghiệm trang 42 Toán 11 Tập 2: Đo góc giữa một sợi dây kéo căng và mặt bàn hoặc sàn lớp học. (Có thể cho một đầu dây thuộc mặt bàn, mặt sàn để thuận tiện hơn cho việc đo).

Lời giải:

Để đo góc giữa một sợi dây kéo căng và mặt bàn hoặc sàn lớp học ta có thể làm như sau:

Bước 1: Đặt một đầu dây lên mặt bàn hoặc sàn lớp học và giữ cho sợi dây căng thẳng.

Bước 2: Xác định hình chiếu vuông góc của dây trên mặt bàn hoặc sàn lớp học.

Bước 3: Dùng thước đo góc để đo góc tạo bởi sợi dây và hình chiếu của dây trên mặt bàn hoặc sàn lớp học.

Bước 4: Ghi lại kết quả đo.

Bài tập

Bài 7.10 trang 42 Toán 11 Tập 2: Cho hình chóp S.ABC có $SA\perp \left(ABC\right)$, tam giác ABC vuông tại B.

a) Xác định hình chiếu của điểm S trên mặt phẳng (ABC).

b) Xác định hình chiếu của tam giác SBC trên mặt phẳng (ABC).

c) Xác định hình chiếu của tam giác SBC trên mặt phẳng (SAB).

Lời giải:

a) Vì SA ⊥ (ABC) nên A là hình chiếu của S trên mặt phẳng (ABC).

b) Có A là hình chiếu của S trên mặt phẳng (ABC),

B là hình chiếu của B trên mặt phẳng (ABC),

C là hình chiếu của C trên mặt phẳng (ABC).

Do đó hình chiếu của tam giác SBC trên mặt phẳng (ABC) là tam giác ABC.

c) Có SA ⊥ (ABC) nên SA ⊥ BC.

Vì tam giác ABC vuông tại B nên AB ⊥ BC.

Do AB ⊥ BC và SA ⊥ BC nên BC ⊥ (SAB), suy ra B là hình chiếu của C trên mặt phẳng (SAB).

B là hình chiếu của B trên mặt phẳng (SAB), S là hình chiếu của S trên mặt phẳng (SAB).

Do đó hình chiếu của tam giác SBC trên mặt phẳng (SAB) là SB.

Bài 7.11 trang 42 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA ⊥ (ABCD) và $SA=a\sqrt{2}$.

a) Tính góc giữa SC và mặt phẳng (ABCD).

b) Tính góc giữa BD và mặt phẳng (SAC).

c) Tìm hình chiếu của SB trên mặt phẳng (SAC).

Lời giải:

a) Vì SA ⊥ (ABCD) nên A là hình chiếu của S trên mặt phẳng (ABCD).

Do đó AC là hình chiếu của SC trên mặt phẳng (ABCD).

Khi đó góc giữa SC và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng AC và SC, mà (AC, SC) = $\widehat{SCA}$.

Vì ABCD là hình vuông cạnh a nên $AC=\sqrt{A{B}^2+B{C}^2}=a\sqrt{2}$.

Vì SA ⊥ (ABCD) nên SA ⊥ AC.

Xét tam giác SAC vuông tại A và SA = AC = $a\sqrt{2}$ nên tam giác SAC vuông cân tại A, suy ra $\widehat{SCA}=45°$.

Vậy góc giữa SC và mặt phẳng (ABCD) bằng 45°.

b) Vì SA ⊥ (ABCD) nên SA ⊥ BD.

Do ABCD là hình vuông nên AC ⊥ BD.

Vì SA ⊥ BD và AC ⊥ BD nên BD ⊥ (SAC).

Do đó góc giữa BD và mặt phẳng (SAC) bằng 90°.

c) Gọi O là giao điểm của AC và BD và ABCD là hình vuông, suy ra BO ⊥ AC.

Mà SA ⊥ (ABCD) nên SA ⊥ BO.

Vì SA ⊥ BO và BO ⊥ AC nên BO ⊥ (SAC), suy ra O là hình chiếu của B trên mặt phẳng (SAC).

Có S là hình chiếu của S trên mặt phẳng (SAC).

Do đó SO là hình chiếu của SB trên mặt phẳng (SAC).

Bài 7.12 trang 42 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), tam giác ABC vuông tại B, SA = AB = BC = a.

a) Xác định hình chiếu của A trên mặt phẳng (SBC).       

b) Tính góc giữa SC và mặt phẳng (ABC).

Lời giải:

a) Kẻ AD ⊥ SB tại D.

Vì SA ⊥ (ABC) nên SA ⊥ BC.

Do ABC là tam giác vuông tại B nên AB ⊥ BC mà SA ⊥ BC, suy ra BC ⊥ (SAB).

Vì BC ⊥ (SAB) nên BC ⊥ AD mà AD ⊥ SB nên AD ⊥ (SBC).

Vậy D là hình chiếu của A trên mặt phẳng (SBC).

b) Vì SA ⊥ (ABC) nên AC là hình chiếu của SC trên mặt phẳng (ABC).

Khi đó góc giữa SC và mặt phẳng (ABC) bằng góc giữa hai đường thẳng AC và SC, mà (AC, SC) = $\widehat{SCA}$.

Xét tam giác ABC vuông tại B có: $AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$.

Vì SA ⊥ (ABC) nên SA ⊥ AC.

Xét tam giác SAC vuông tại A, có $\tan \widehat{SCA}=\frac{SA}{AC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$ $\Rightarrow \widehat{SCA}=35,26°$.

Vậy góc giữa SC và mặt phẳng (ABC) khoảng 35,26°.

Giải Toán 11 trang 43 Tập 2

Bài 7.13 trang 43 Toán 11 Tập 2: Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi đểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng:

a) Hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau;

b) Đường xiên SM lớn hơn đường xiên SM' nếu hình chiếu HM lớn hơn hình chiếu HM'.

Lời giải:

a) Có H là hình chiếu của S trên mặt phẳng (P) nên SH ⊥ (P), suy ra SH ⊥ HM, SH ⊥ HM'.

- Giả sử SM = SM'.

Xét tam giác SHM vuông tại H, có SM² = SH² + HM²

Xét tam giác SHM' vuông tại H, có SM'² = SH² + HM'².

Mà SM = SM' nên HM = HM'.

- Giả sử HM = HM'.

Xét tam giác SHM vuông tại H, có SM² = SH² + HM²

Xét tam giác SHM' vuông tại H, có SM'² = SH² + HM'².

Mà HM = HM' nên SM = SM'.

Vậy hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau.

b) Trên tia HM lấy điểm N sao cho SN = SM' suy ra HN = HM'.

Mà SM > SM' nên SM > SN ⇒ HM > HN hay HM > HM'.

Bài 7.14 trang 43 Toán 11 Tập 2: Trong một khoảng thời gian đầu kể từ khi cất cánh, máy bay bay theo một đường thẳng. Góc cất cánh của nó là góc giữa đường thẳng đó và mặt phẳng nằm ngang nơi cất cánh. Hai máy bay cất cánh và bay thẳng với cùng độ lớn vận tốc trong 5 phút đầu, với các góc cất cánh lần lượt là 10°, 15°. Hỏi sau 1 phút kể từ khi cất cánh, máy bay nào ở độ cao so với mặt đất (phẳng, nằm ngang) lớn hơn?

Chú ý. Độ cao của máy bay so với mặt đất là khoảng cách từ máy bay (coi là một điểm) đến hình chiếu của nó trên mặt đất.

Lời giải:

Hai máy bay có cùng độ lớn vận tốc nên sau 1 phút kể từ khi cất cánh hai máy bay bay được quãng đường bằng nhau tức AM = A'M'.

Xét tam giác ABM vuông tại B có BM = AM × sin10°

Xét tam giác A'CM' vuông tại C có CM' = A'M' × sin15°.

Mà sin10° < sin15° nên BM < CM'.

Vậy sau 1 phút cất cánh, máy bay có góc cất cánh 15° ở độ cao lớn hơn so với máy bay có góc cất cánh 10°.

Bài 7.15 trang 43 Toán 11 Tập 2: Hãy nêu cách đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm.

Chú ý. Góc giữa đường thẳng chứa tia sáng mặt trời lúc giữa trưa với mặt phẳng nằm ngang tại vị trí đó được gọi là góc Mặt Trời. Giữa trưa là thời điểm ban ngày mà tâm Mặt Trời thuộc mặt phẳng chứa kinh tuyến đi qua điểm đang xét. Góc Mặt Trời ảnh hưởng tới sự hấp thụ nhiệt từ Mặt Trời của Trái Đất, tạo nên các mùa trong năm trên Trái Đất.

Lời giải:

Để đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm ta đưa về bài toán trên sân phẳng có một cây cột AB vuông góc với mặt sân, dưới ánh sáng mặt trời, bóng của cây cột trên sân AM chính là hình chiếu của cây cột. Khi đó góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang chính là góc $\widehat{BMA}$.

Xét tam giác BAM vuông tại A, có: $\tan \widehat{BMA}=\frac{AB}{AM}$.

Từ đó ta tính được góc BMA.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 25: Hai mặt phẳng vuông góc

Bài 26: Khoảng cách

Bài 27: Thể tích

Lý thuyết Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

1. Phép chiếu vuông góc

Phép chiếu vuông góc lên mặt phẳng (P) theo phương $\mathrm{\Delta }$ vuông góc với (P) được gọi là phép chiều vuông góc lên mặt phẳng (P).

Chú ý:

- Vì phép chiếu vuông góc lên một mặt phẳng là một trường hợp đặc biệt của phép chiếu song song nên nó có mọi tính chất của phép chiếu song song.

- Phép chiếu vuông góc lên mặt phẳng (P) còn được gọi đơn giản là phép chiếu lên mặt phẳng (P). Hình chiếu vuông góc H’ của hình H trên mặt phẳng (P) còn được gọi là hình chiếu của H trên mặt phẳng (P).

Định lí ba đường vuông góc:

Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Khi đó, một đường thẳng b nằm trong mặt phẳng (P) vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu vuông góc a’ của a trên (P).

2. Góc giữa đường thẳng và mặt phẳng

Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng ${90}^0$.

Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).

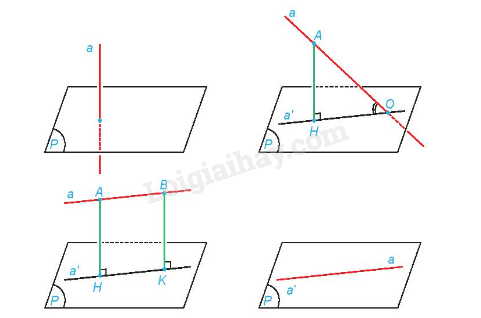
Chú ý: Nếu $\alpha$ là góc giữa đường thẳng a và mặt phẳng (P) thì $0^0\le \alpha \le {90}^0$.

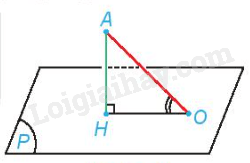
Nhận xét: Nếu điểm A có hình chiếu H trên mặt phẳng (P). Lấy điểm O thuộc mặt phẳng (P), O không trung H. Khi đó góc giữa đường thẳng AO và mặt phẳng (P) bằng góc AOH.