Với lời giải Toán 8 trang 102 Tập 1 chi tiết Bài 3: Hình thang cân sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 Bài 3: Hình thang cân

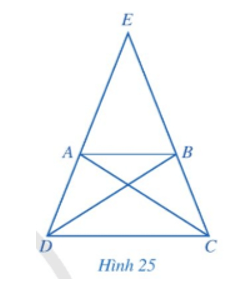
Hoạt động 3 trang 102 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, AB < CD, E là giao điểm của AD và BC (Hình 25).

a) So sánh các cặp góc: $\widehat{EDC}$ và $\widehat{ECD}$; $\widehat{EAB}$ và $\widehat{EBA}$.

b) So sánh các cặp đoạn thẳng: EA và EB; ED và EC. Từ đó, hãy so sánh AD và BC.

c) Hai tam giác ADC và BCD có bằng nhau hay không? Từ đó, hãy so sánh AC và BD.

Lời giải:

a) Do ABCD là hình thang cân nên $\widehat{ADC}=\widehat{BCD}$ và $\widehat{DAB}=\widehat{CBA}\left(1\right)$.

Do $\widehat{ADC}=\widehat{BCD}$ nên $\widehat{EDC}=\widehat{ECD}$.

Ta lại có $\widehat{DAB}+\widehat{EAB}=180°$ (hai góc kề bù)

Suy ra $\widehat{EAB}=180°-\widehat{DAB}\left(2\right)$   

Tương tự ta cũng có $\widehat{EBA}=180°-\widehat{CBA}\left(3\right)$

Từ (1), (2) và (3) ta có $\widehat{EAB}=\widehat{EBA}$.

b) • Xét tam giác EAB có $\widehat{EAB}=\widehat{EBA}$ (câu a) nên là tam giác cân tại E

Suy ra EA = EB.

• Xét tam giác EDC có $\widehat{EDC}=\widehat{ECD}$ (câu a) nên là tam giác cân tại E

Suy ra ED = EC.

• Ta có AD = ED – EA

            BC = EC – EB.

Mặt khác EA = EB và ED = EC

Do đó AD = BC.

c) Xét ΔADC và ΔBCD có:

AD = BC (theo câu b);

$\widehat{ADC}=\widehat{BCD}$ (theo câu a);

DC là cạnh chung

Do đó ΔADC = ΔBCD (c.g.c)

Suy ra AC = BD (hai cạnh tương ứng).

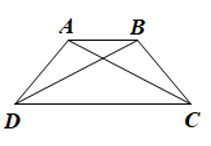
Luyện tập 1 trang 102 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD. Chứng minh $\widehat{ADB}=\widehat{BCA}$.

Lời giải:

Do ABCD là hình thang cân (AB // CD) nên AD = BC và AC = BD.

Xét ΔADB và ΔBCA có:

AB là cạnh chung;

AD = BC (chứng minh trên);

BD = AC (chứng minh trên)

Do đó ΔADB = ΔBCA (c.c.c)

Suy ra $\widehat{ADB}=\widehat{BCA}$ (hai cạnh tương ứng).

III. Dấu hiệu nhận biết

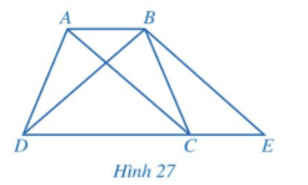
Hoạt động 4 trang 102, 103 Toán 8 Tập 1: Quan sát hình thang ABCD (AB // CD, AB < CD) có hai đường chéo AC và BD bằng nhau. Kẻ BE song song với AC (E thuộc đường thẳng CD) (Hình 27).

a) Hai tam giác ABC và ECB có bằng nhau hay không?

b) So sánh các cặp góc: $\widehat{BED}$ và $\widehat{BDE}$ và $\widehat{ACD}$ và $\widehat{BED}$.

c) Hai tam giác ACD và BDC có bằng nhau hay không? Từ đó, hãy so sánh $\widehat{ADC}$ và $\widehat{BCD}$.

d) ABCD có phải là hình thang cân hay không?

Lời giải:

a) Do AB // CD hay AB // CE nên $\widehat{ABC}=\widehat{ECB}$ (so le trong).

Do BE // AC nên $\widehat{ACB}=\widehat{EBC}$ (so le trong).

Xét ΔABC và ΔECB có:

$\widehat{ABC}=\widehat{ECB}$ (chứng minh trên);

BC là cạnh chung;

$\widehat{ACB}=\widehat{EBC}$ (chứng minh trên).

Do đó ΔABC = ΔECB (g.c.g).

b) Do ΔABC = ΔECB (theo câu a) nên AC = EB (hai cạnh tương ứng)

Mà AC = BD (giả thiết)

Suy ra BD = BE nên tam giác BDE là tam giác cân tại B.

Suy ra $\widehat{BDE}=\widehat{BED}$ (tính chất tam giác cân).

Do BE // AC nên $\widehat{ACD}=\widehat{BED}$ (đồng vị).

c) Ta có $\widehat{BDE}=\widehat{BED}$ và $\widehat{ACD}=\widehat{BED}$ (theo câu b) nên $\widehat{BDE}=\widehat{ACD}\left(=\widehat{BED}\right)$.

Xét ΔACD và ΔBDC có:

DC là cạnh chung;

$\widehat{BDE}=\widehat{ACD}$ (chứng minh trên);

AC = BD (giả thiết)

Do đó ΔACD = ΔBDC (c.g.c)

Suy ra $\widehat{ADC}=\widehat{BCD}$ (hai góc tương ứng).

d) Hình thang ABCD có $\widehat{ADC}$, $\widehat{BCD}$ cùng kề với đáy DC và $\widehat{ADC}=\widehat{BCD}$ nên ABCD là hình thang cân.