Với lời giải Toán 8 trang 17 Tập 1 chi tiết Bài 2: Các phép tính với đa thức nhiều biến sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 Bài 2: Các phép tính với đa thức nhiều biến

Bài 3 trang 17 Toán 8 Tập 1: Rút gọn biểu thức:

a) (x – y)(x² + xy + y²);

b) (x + y)(x² – xy + y²);

c) $(4x-1)(6y+1)-3x\left(8x+\frac{4}{3}\right)$;

d) (x + y)(x – y) + (xy⁴ – x³y²) : (xy²).

Lời giải:

a) (x – y)(x² + xy + y²)

= x . x² + x . xy + x . y²– y . x² – y . xy– y . y²

= x³ + (x²y – x²y) + (xy²– xy²) – y³= x³ – y³.

b) (x + y)(x² – xy + y²)

= x . x² – x . xy + x . y² + y . x² – y . xy + y . y²

= x³ – x²y + xy² + x²y – xy² + y³

= x³ + (x²y – x²y) + (xy²– xy²) + y³

= x³ + y³.

c) (4x - 1)(6y + 1) - 3x$\left(8x+\frac{4}{3}\right)$

= 4x.6y + 4x.1 - 1.6y - 1.1 - 3x.8x - 3x.$\frac{4}{3}$

= 24xy + 4x – 6y – 1 – 24x² – 4x

= 24xy – 24x² + (4x – 4x) – 6y – 1

= 24xy – 24x² – 6y – 1.

d) (x + y)(x – y) + (xy⁴ – x³y²) : (xy²)

= x . x + x . y – x . y – y . y + (xy⁴) : (xy²) – (x³y²) : (xy²)

= x² – y² + y²– x²= (x² – x²) + (y²– y²) = 0.

Bài 4 trang 17 Toán 8 Tập 1: a) Rút gọn rồi tính giá trị của biểu thức.

P = (5x² – 2xy + y²) – (x² + y²) – (4x² – 5xy + 1)

khi x = 1,2 và x + y = 6,2.

b) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x:

(x² – 5x + 4)(2x + 3) – (2x² – x – 10)(x – 3).

Lời giải:

a) Ta rút gọn biểu thức P như sau:

P = (5x² – 2xy + y²) – (x² + y²) – (4x² – 5xy + 1)

= 5x² – 2xy + y²–x² – y²–4x² + 5xy – 1

= (5x² –x² –4x²)+(5xy – 2xy) + (y²– y²) – 1

= 3xy – 1.

Ta có: x = 1,2; x + y = 6,2 suy ra y = 6,2 – x = 6,2 – 1,2 = 5.

Khi đó, giá trị của biểu thức P khi x = 1,2 và y = 5 là:

3 . 1,2 . 5 – 1 = 18 – 1 = 17.

b) Ta có: (x² – 5x + 4)(2x + 3) – (2x² – x – 10)(x – 3)

= (2x³ – 10x²+ 8x + 3x²– 15x + 12) –(2x³ – x² – 10x – 6x² + 3x + 30)

= (2x³ – 7x²– 7x+ 12) – (2x³ – 7x² – 7x + 30)

= 2x³ – 7x²– 7x+ 12–2x³ +7x²+ 7x – 30

= (2x³ – 2x³) +(7x² – 7x²) +(7x – 7x) + (12– 30) = –8.

Khi đó, với mọi giá trị của biến x thì (x² – 5x + 4)(2x + 3) – (2x² – x – 10)(x – 3)= –8.

Vậy giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

Bài 5 trang 17 Toán 8 Tập 1: a) Chứng minh rằng biểu thức P = 5x(2 – x) – (x + 1)(x + 9) luôn nhận giá trị âm với mọi giá trị của biến x.

b) Chứng minh rằng biểu thức Q = 3x² + x(x – 4y) – 2x(6 – 2y) + 12x + 1 luôn nhận giá trị dương với mọi giá trị của biến x và y.

Lời giải:

a) Ta có: P = 5x(2 – x) – (x + 1)(x + 9)

= (10x – 5x²) – (x² + x + 9x + 9)

= (10x – 5x²) – (x² + 10x + 9)

= 10x – 5x² – x² – 10x – 9

= (– 5x² – x²) + (10x – 10x) – 9 = – 9.

Khi đó, với mọi giá trị của biến x thì P = – 9.

Vậy biểu thức P luôn nhận giá trị âm với mọi giá trị của biến x.

b) Ta có: Q = 3x² + x(x – 4y) – 2x(6 – 2y) + 12x + 1

= 3x² + x² – 4xy – 12x + 4xy + 12x + 1

= (3x² + x²) + (4xy – 4xy) + (12x – 12x) + 1

= 4x² + 1

Vì 4x²≥ 0 nên 4x² + 1 > 0.

Vậy biểu thức Q luôn nhận giá trị dương với mọi giá trị của biến x và y.

Bài 6 trang 17 Toán 8 Tập 1: Bạn Hạnh dự định cắt một miếng bìa có dạng tam giác vuông với độ dài hai cạnh góc vuông lần lượt là 6 (cm), 8 (cm). Sau khi xem xét lại, bạn Hạnh quyết định tăng độ dài cạnh góc vuông 6 (cm) thêm x (cm) và tăng độ dài cạnh góc vuông 8 (cm) thêm y (cm) (Hình 3). Viết đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y...

Lời giải:

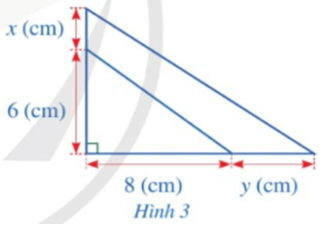
Diện tích tam giác vuông ban đầu là: $\frac{1}{2}$.6.8 = 24 (cm)

Tam giác vuông sau khi mở rộng có độ dài hai cạnh góc vuông lần lượt là x + 6 (cm); y + 8 (cm).

Diện tích tam giác vuông sau khi tăng độ dài hai cạnh góc vuông là:

$\frac{1}{2}$.(x+6).(y+8) = $\frac{1}{2}$xy + 4x + 3y + 24

= 24 + 4x + 3y + 24 = 4x + 3y + 48 (cm)

Vậy đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y là: 4x + 3y + 48 (cm).

Bài 7 trang 17 Toán 8 Tập 1: Khu vực của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (Hình 4). Biết diện tích của mảnh đất không trồng rau bằng 475 m². Tính độ dài x (m) của khu vườn đó.

Lời giải:

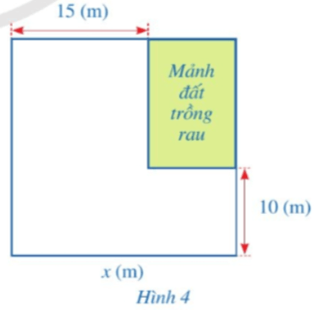
Trong Hình 4, ta thấy:

• Khu vực nhà bác Xuân là hình vuông có cạnh x (m)

Diện tích khu vực nhà bác Xuân là: x² (m²).

• Mảnh đất trồng rau có dạng hình chữ nhật có chiều dài bằng x – 10 (m) và chiều rộng bằng x – 15 (m).

Diện tích mảnh đất trồng rau là: (x – 10)(x – 15) = x² – 10x – 15x + 150

= x² – 25x + 150 (m²).

Theo đề bài, diện tích của mảnh đất không trồng rau bằng 475 m² nên ta có:

x² – (x² – 25x + 150) 475

x² – x² + 25x – 150 = 475

25x – 150 = 475

25x = 625

x = 25.

Vậy khu vườn có độ dài 25 m.