Với giải sách bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 1: Bất phương trình bậc nhất hai ẩn
Giải SBT Toán 10 trang 27 Tập 1
Bài 1 trang 27 SBT Toán 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn: 2x – 5y + 10 > 0.
a) Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng Oxy.
b) (1; 3) có phải là nghiệm của bất phương trình trên không?
c) Chỉ ra 2 cặp số (x; y) thỏa mãn bất phương trình trên.
Lời giải:
a) Vẽ đường thẳng 2x – 5y + 10 = 0.
Cho x = 0, khi đó 2 . 0 – 5y + 10 = 0, suy ra y = 2.
Cho y = 0, khi đó 2x – 5 . 0 + 10 = 0, suy ra x = – 5.
Do đó, đường thẳng 2x – 5y + 10 = 0 đi qua hai điểm (0; 2) và (– 5; 0).
Lấy điểm O(0; 0) không thuộc đường thẳng 2x – 5y + 10 = 0.
Ta có: 2 . 0 – 5 . 0 + 10 = 10 > 0, do đó tọa độ điểm O thỏa mãn bất phương trình 2x – 5y + 10 > 0.
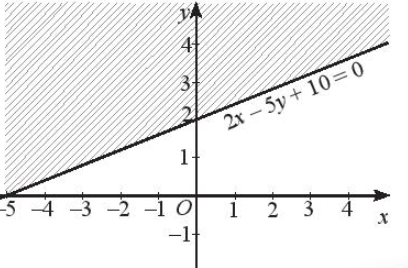
Vậy miền nghiệm của bất phương trình 2x – 5y + 10 > 0 là nửa mặt phẳng có bờ là đường thẳng 2x – 5y + 10 = 0, chứa gốc O và không kể đường thẳng 2x – 5y + 10 = 0 (miền không bị gạch trong hình dưới đây).
b) Thay x = 1, y = 3 vào biểu thức 2x – 5y + 10, ta được:
2 . 1 – 5 . 3 + 10 = – 3 < 0
Do đó, cặp số (1; 3) không thỏa mãn bất phương trình 2x – 5y + 10 > 0.
Vậy (1; 3) không là nghiệm của bất phương trình đã cho.
c) Ta chọn cặp số (x; y) tùy ý sao cho 2x – 5y + 10 > 0.
Chẳng hạn các cặp số (1; 2) và (3; 3) thỏa mãn bất phương trình đã cho.
Do 2 . 1 – 5 . 2 + 10 = 2 > 0 và 2 . 3 – 5 . 3 + 10 = 1 > 0.
a) x + y – 1 > 0;
Lời giải:
a) Vẽ đường thẳng x + y – 1 = 0.
Cho x = 0, khi đó 0 + y – 1 = 0, suy ra y = 1.
Cho y = 0, khi đó x + 0 – 1 = 0, suy ra x = 1.
Do đó, đường thẳng x + y – 1 = 0 đi qua hai điểm (0; 1) và (1; 0).
Lấy điểm O(0; 0) không thuộc đường thẳng x + y – 1 = 0.
Ta có: 0 + 0 – 1 = – 1 < 0, do đó tọa độ điểm O không thỏa mãn bất phương trình x + y – 1 > 0.
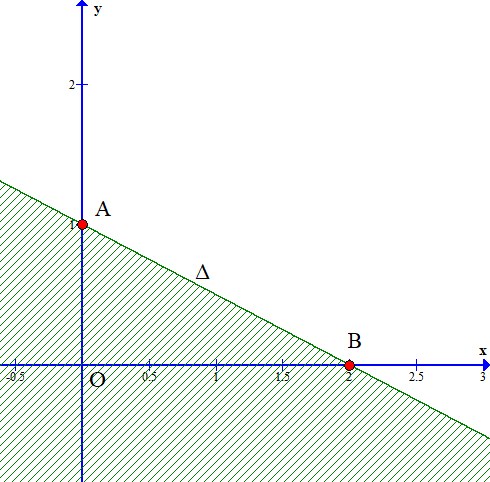
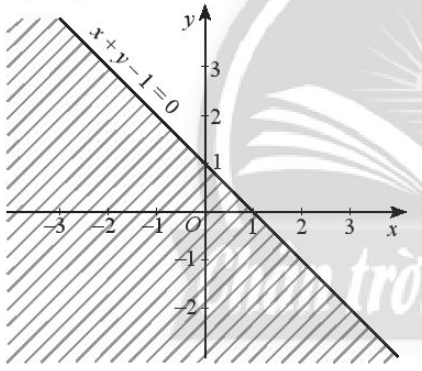
Vậy miền nghiệm của bất phương trình x + y – 1 > 0 là nửa mặt phẳng có bờ là đường thẳng x + y – 1 = 0, không chứa gốc O và không kể đường thẳng x + y – 1 = 0 (miền không bị gạch trong hình dưới đây).
b) Vẽ đường thẳng x – 1 = 0. (chính là đường thẳng x = 1, đi qua điểm (1; 0) và song song với trục Oy).
Lấy điểm O(0; 0) không thuộc đường thẳng x – 1 = 0.
Ta có: 0 – 1 = – 1 < 0, do đó tọa độ điểm O không thỏa mãn bất phương trình x – 1 ≥ 0.
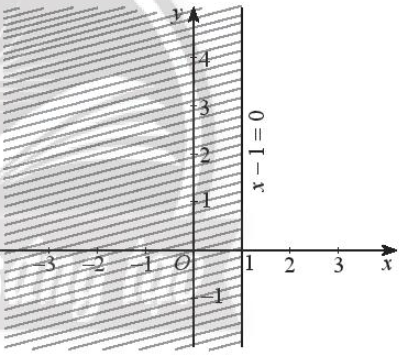
Vậy miền nghiệm của bất phương trình x – 1 ≥ 0 là nửa mặt phẳng có bờ là đường thẳng x – 1 = 0, không chứa gốc O và kể cả đường thẳng x – 1 = 0 (miền không bị gạch trong hình dưới đây).
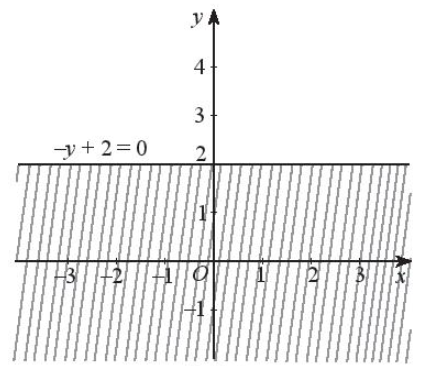
c) Vẽ đường thẳng – y + 2 = 0. (chính là đường thẳng y = 2, đi qua điểm (0; 2) và song song với trục Ox).
Lấy điểm O(0; 0) không thuộc đường thẳng – y + 2 = 0.
Ta có: – 0 + 2 = 2 > 0, do đó tọa độ điểm O không thỏa mãn bất phương trình – y + 2 ≤ 0.
Vậy miền nghiệm của bất phương trình – y + 2 ≤ 0 là nửa mặt phẳng có bờ là đường thẳng – y + 2 = 0, không chứa gốc O và kể cả đường thẳng – y + 2 = 0 (miền không bị gạch trong hình dưới đây).
a) 3x + 2y < x – y + 8;
Lời giải:
a) 3x + 2y < x – y + 8
⇔ 3x – x + 2y + y < 8
⇔ 2x + 3y < 8.
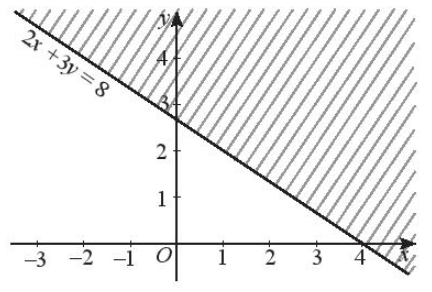
Vẽ đường thẳng 2x + 3y = 8.
Cho x = 0, khi đó 2 . 0 + 3y = 8, suy ra y = .
Cho y = 0, khi đó 2x + 3 . 0 = 8, suy ra x = 4.
Do đó, đường thẳng 2x + 3y = 8 đi qua hai điểm và (4; 0).
Lấy điểm O(0; 0) không thuộc đường thẳng 2x + 3y = 8.
Ta có: 2 . 0 + 3 . 0 = 0 < 8, do đó tọa độ điểm O thỏa mãn bất phương trình 2x + 3y < 8.
Vậy miền nghiệm của bất phương trình 2x + 3y < 8 là nửa mặt phẳng có bờ là đường thẳng 2x + 3y = 8, chứa gốc O và không kể đường thẳng 2x + 3y = 8 (miền không bị gạch trong hình dưới đây).
b) 2(x – 1) + 3(y – 2) > 2
⇔ 2x – 2 + 3y – 6 > 2
⇔ 2x + 3y > 10.
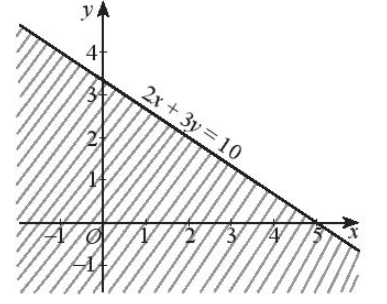
Vẽ đường thẳng 2x + 3y = 10.
Cho x = 0, khi đó 2 . 0 + 3y = 10, suy ra y = .
Cho y = 0, khi đó 2x + 3 . 0 = 10, suy ra x = 5.
Do đó, đường thẳng 2x + 3y = 10 đi qua hai điểm và (5; 0).
Lấy điểm O(0; 0) không thuộc đường thẳng 2x + 3y = 10.
Ta có: 2 . 0 + 3 . 0 = 0 < 10, do đó tọa độ điểm O không thỏa mãn bất phương trình 2x + 3y > 10.
Vậy miền nghiệm của bất phương trình 2x + 3y > 10 là nửa mặt phẳng có bờ là đường thẳng 2x + 3y = 10, không chứa gốc O và không kể đường thẳng 2x + 3y = 10 (miền không bị gạch trong hình dưới đây).
Lời giải:
Do x, y lần lượt là số lít nước rửa xe loại I và II pha chế được nên x ≥ 0, y ≥ 0.
Để pha chế x lít nước rửa xe loại I, Nga cần số ml dung dịch chất tẩy rửa là: 600x (ml).
Để pha chế y lít nước rửa xe loại II, Nga cần số ml dung dịch chất tẩy rửa là: 400y (ml).
Tổng số ml dung dịch chất tẩy rửa Nga dùng để pha chế x lít nước rửa xe loại I và y lít nước rửa xe loại II là 600x + 400y.
Mà Nga chỉ có 2 400 ml dung dịch chất tẩy rửa nên 600x + 400y ≤ 2 400 ⇔ 3x + 2y ≤ 12.
Vậy các bất phương trình mô tả số lít nước rửa xe loại I và loại II mà bạn Nga có thể pha chế được là: x ≥ 0, y ≥ 0, 3x + 2y ≤ 12.
Ta biểu diễn miền nghiệm của các bất phương trình trên.
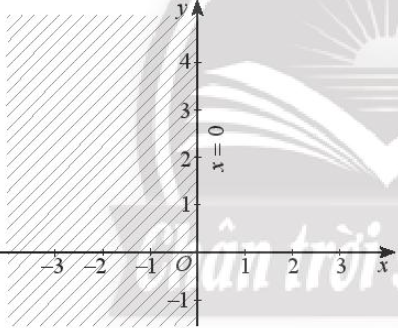
+ Bất phương trình x ≥ 0:
Miền nghiệm của bất phương trình này chính là nửa mặt phẳng có bờ là đường thẳng Oy, nằm bên phải trục Oy, bao gồm cả đường thẳng Oy (miền không bị gạch trong hình dưới đây).
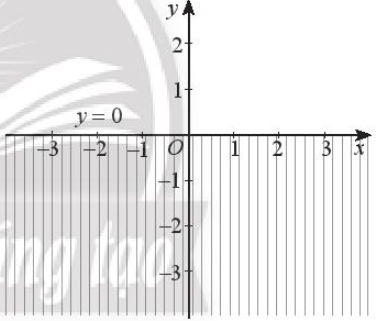
+ Bất phương trình y ≥ 0:
Miền nghiệm của bất phương trình này chính là nửa mặt phẳng có bờ là đường thẳng Ox, nằm bên trên trục Ox, bao gồm cả đường thẳng Ox (miền không bị gạch trong hình dưới đây).
+ Bất phương trình 3x + 2y ≤ 12:
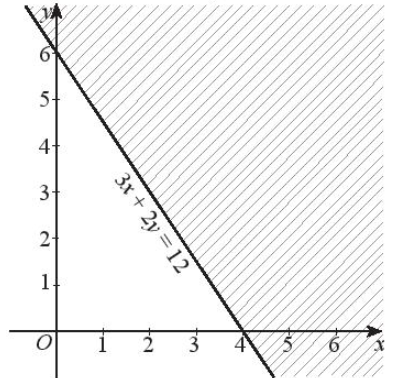
Vẽ đường thẳng 3x + 2y = 12.
Cho x = 0, khi đó 3 . 0 + 2y = 12, suy ra y = 6.
Cho y = 0, khi đó 3x + 2 . 0 = 12, suy ra x = 4.
Do đó, đường thẳng 3x + 2y = 12 đi qua hai điểm (0; 6) và (4; 0).
Lấy điểm O(0; 0) không thuộc đường thẳng 3x + 2y = 12.
Ta có: 3 . 0 + 2 . 0 = 0 < 12, do đó tọa độ điểm O thỏa mãn bất phương trình 3x + 2y ≤ 12.
Vậy miền nghiệm của bất phương trình 3x + 2y ≤ 12 là nửa mặt phẳng có bờ là đường thẳng 3x + 2y = 12, chứa gốc O và kể cả đường thẳng 3x + 2y = 12 (miền không bị gạch trong hình dưới đây).
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Lý thuyết Bất phương trình bậc nhất hai ẩn
1. Khái niệm bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng
ax + by + c < 0; ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0,
trong đó a, b, c là những số cho trước, a, b không đồng thời bằng 0, x và y là các ẩn.
Ví dụ:
5x + 2y < 4 là bất phương trình bậc nhất hai ẩn vì bất phương trình chứa hai ẩn x, y ở bậc nhất.
5x + 2y – 3z > 3 không là bất phương trình bậc nhất hai ẩn vì bất phương trình này chứa 3 ẩn x, y, z ở bậc nhất.
2. Nghiệm của bất phương trình bậc nhất hai ẩn
Xét bất phương trình ax + by + c < 0.
Mỗi cặp số (x0; y0) thỏa mãn ax0 + by0 + c < 0 được gọi là một nghiệm của bất phương trình đã cho.
Chú ý: Nghiệm của các bất phương trình ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0 được định nghĩa tương tự.
Ví dụ:
+ Bất phương trình bậc nhất hai ẩn 5x + 2y < 4 có các cặp nghiệm là (-1; -2); (0; 0); bởi:
Với x = ‒1, y = ‒2 ta có: 5.(‒1) + 2.(‒2) = ‒9 < 4 nên (‒1; ‒2) là nghiệm của bất phương trình 5x + 2y < 4.
Với x = 0, y = 0 ta có: 5. 0 + 2. 0 = 0 < 4 nên (0; 0) là nghiệm của bất phương trình 5x + 2y < 4.
+ Bất phương trình bậc nhất hai ẩn x ‒ 2y ≥ 4 có các cặp nghiệm là (4; ‒1); (4; 0); bởi:
Với x = 4, y = ‒1 ta có: 4 – 2. (‒1) = 6 ≥ 4 nên (4; ‒1) là nghiệm của bất phương trình x ‒ 2y ≥ 4.
Với x = 4, y = 0 ta có: 4 ‒ 2. 0 = 4 ≥ 4 nên (4; 0) là nghiệm của bất phương trình x ‒ 2y ≥ 4.
3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x0; y0) sao cho ax0 + by0 + c < 0 được gọi là miền nghiệm của bất phương trình ax + by + c < 0.
- Người ta chứng minh được: Mỗi phương trình ax + by + c = 0 (a, b không đồng thời bằng 0) xác định một đường thẳng ∆. Đường thẳng ∆ chia mặt phẳng tọa độ Oxy thành hai nửa mặt phẳng, trong đó một nửa (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c > 0, nửa còn lại (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c < 0.
Ta có thể biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by + c < 0 như sau:
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: ax + by +c = 0.
Bước 2: Lấy một điểm (x0; y0) không thuộc ∆. Tính ax0 +by0 + c.
+ Nếu ax0 + by0 + c < 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (x0; y0).
+ Nếu ax0 + by0 + c > 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (x0; y0).
Chú ý: Đối với các bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 (hoặc ax + by + c ≥ 0) thì miền nghiệm là miền nghiệm của bất phương trình ax + by + c < 0 (hoặc ax + by + c > 0) kể cả bờ.
Ví dụ: Biểu diễn miền nghiệm của bất phương trình x + 2y – 2 > 0 trên mặt phẳng tọa độ:
Bước 1: Vẽ đường thẳng ∆: x + 2y – 2 = 0 trên mặt phẳng tọa độ Oxy.
Bước 2: Lấy điểm O (0; 0) không thuộc ∆ và thay x = 0 và y = 0 vào biểu thức x + 2y – 2 ta được 0 + 2.0 – 2 = ‒2 > 0 là mệnh đề sai.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ ∆ (không kể bờ ∆) không chứa điểm O (miền nghiệm là miền không bị gạch trên hình)