Với giải sách bài tập Toán 10 Bài 2: Tập hợp sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 2: Tập hợp

Giải SBT Toán 10 trang 13 Tập 1

Bài 1 trang 13 SBT Toán 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {x | x² – 2x – 15 = 0};

b) B = {x ∈ ℤ | – 3 < x ≤ 2};

c) C = $\left\{\frac{n}{n^2-1}|n\in \mathbb{N},1<n\le 4\right\}$;

d) D = {(x; y) | x ≤ 2, y < 2, x, y ∈ ℕ}.

Lời giải:

a) Giải phương trình x² – 2x – 15 = 0 ta được hai nghiệm là x = – 3 và x = 5.

Do đó, A = {– 3; 5}.

b) Vì x ∈ ℤ và – 3 < x ≤ 2 nên x là các số nguyên lớn hơn – 3 và nhỏ hơn hoặc bằng 2, đó là các số: – 2; – 1; 0; 1; 2.

Do đó, B = {– 2; – 1; 0; 1; 2}.

c) Ta có n là số tự nhiên lớn hơn 1 và nhỏ hơn hoặc bằng 4, đó là các số: 2; 3; 4.

Với n = 2, ta có $\frac{n}{n^2-1}=\frac{2}{2^2-1}=\frac{2}{4-1}=\frac{2}{3}$.

Với n = 3, ta có $\frac{n}{n^2-1}=\frac{3}{3^2-1}=\frac{3}{9-1}=\frac{3}{8}$.

Với n = 4, ta có $\frac{n}{n^2-1}=\frac{4}{4^2-1}=\frac{4}{16-1}=\frac{4}{15}$.

Do đó, C = $\left\{\frac{2}{3};\frac{3}{8};\frac{4}{15}\right\}$.

d) Ta có x và y là các số tự nhiên, x nhỏ hơn hoặc bằng 2 nên x là các số 0; 1; 2, y nhỏ hơn 2 nên y là các số 0; 1.

Vậy ta có các cặp số (x; y) thỏa mãn D là: (0; 0); (0; 1); (1; 0); (1; 1); (2; 0); (2; 1).

Do đó, D = {(0; 0); (0; 1); (1; 0); (1; 1); (2; 0); (2; 1)}.

Bài 2 trang 13 SBT Toán 10 Tập 1: Viết các tập hợp sau đây bằng cách chỉ ra tính chất đặc trưng của các phần tử:

a) A = {– 4; – 3; – 2; – 1; 0; 1; 2; 3; 4};

b) B = {0; 2; 4; 6; 8; 10};

c) C = $\left\{1;\frac{1}{2};\frac{1}{3};\frac{1}{4};\frac{1}{5}\right\}$;

d) Tập hợp D các số thực lớn hơn hoặc bằng 3 và bé hơn 8.

Lời giải:

a) Các số – 4; – 3; – 2; – 1; 0; 1; 2; 3; 4 là các số nguyên lớn hơn hoặc bằng – 4 và bé hơn hoặc bằng 4.

Do đó, A = {x ∈ ℤ | – 4 ≤ x ≤ 4}.

Ngoài ra, ta có thể viết tập hợp A bằng các cách như sau:

A = {x ∈ ℤ | |x| ≤ 4} hoặc A = {x ∈ ℤ | |x| < 5}.

b) Các số 0; 2; 4; 6; 8; 10 là các số tự nhiên chẵn nhỏ hơn hoặc băng 10.

Do đó, B = {x | x ∈ ℕ, x chẵn, x ≤ 10} hoặc B = {x | x = 2k, k = 0; 1; 2; 3; 4; 5}.

 c) Ta có: 1 = $\frac{1}{1}$.

Do đó, C = $\left\{\frac{1}{n}|n=1;2;3;4;5\right\}$ hoặc C = $\left\{x|x=\frac{1}{n},n\in \mathbb{N},1\le n\le 5\right\}$.

d) D là tập hợp các số thực lớn hơn hoặc bằng 3 và bé hơn 8.

Do đó, D = {x ∈ ℝ | 3 ≤ x < 8}.

Bài 3 trang 13 SBT Toán 10 Tập 1: Điền kí hiệu (∈, ∉, ⊂, ⊄, =) thích hợp vào chỗ chấm.

a) 0 ... {0; 1; 2};

b) {0; 1} ... ℤ;

c) 0 ... {x | x² = 0};

d) {0} ... {x | x² = x};

e) ∅ ... {x ∈ ℝ | x² + 4 = 0};

g) {4; 1} ... {x | x² – 5x + 4 = 0};

h) {n; a; m} ... {m; a; n};

i) {nam} ... {n; a; m}.

Lời giải:

Kí hiệu ∈ (thuộc), ∉ (không thuộc) dùng để chỉ mối quan hệ giữa phần tử và tập hợp.

Kí hiệu ⊂ (tập con), ⊄ (không là tập con) dùng để chỉ mối quan hệ giữa hai tập hợp.

Kí hiệu = dùng để chỉ hai phần tử bằng nhau hoặc hai tập hợp bằng nhau.

a) 0 là một phần tử của tập {0; 1; 2}.

Do đó, 0 ∈ {0; 1; 2}.

b) {0; 1} là một tập hợp gồm hai phần tử là các số nguyên 0; 1 nên {0; 1} là tập con của tập số nguyên ℤ.

Do đó, {0; 1} ⊂ ℤ.

c) Ta có: x² = 0 ⇔ x = 0 nên {x | x² = 0} = {0}.

Do đó, 0 ∈ {x | x² = 0}.

d) Ta có: x² = x ⇔ x² – x = 0 ⇔ x(x – 1) = 0 ⇔ x = 0 hoặc x = 1.

Suy ra {x | x² = x} = {0; 1}.

Tập hợp {0} chứa phần tử 0 là một phần tử của tập hợp {0; 1}.

Do đó, {0} ⊂ {x | x² = x}.

e) Với mọi số thực x, ta có x² + 4 > 0 nên phương trình x² + 4 = 0 vô nghiệm.

Suy ra {x ∈ ℝ | x² + 4 = 0} = ∅.

Hay ∅ = {x ∈ ℝ | x² + 4 = 0}.

g) Ta có: x² – 5x + 4 = 0 ⇔ x² – x – 4x + 4 = 0

⇔ x(x – 1) – 4(x – 1) = 0 ⇔ (x – 1)(x – 4) = 0 ⇔ x = 1 hoặc x = 4.

Suy ra {x | x² – 5x + 4 = 0} = {1; 4}.

Hay {4; 1} = {x | x² – 5x + 4 = 0}.

h) Hai tập hợp {m; a; n} và {m; a; n} đều có các phần tử giống nhau nên đây là hai tập hợp bằng nhau.

Do đó, {n; a; m} = {m; a; n}.

i) Tập hợp {nam} gồm một phần tử là nam, tập hợp {n; a; m} gồm ba phần tử là n, a, m, khác phần tử nam.

Do đó, {nam} ⊄ {n; a; m}.

Bài 4 trang 13 SBT Toán 10 Tập 1: Điền kí hiệu (⊂, ⊃, =) thích hợp vào chỗ chấm.

a) {x | x(x – 1)(x + 1) = 0} ... {x | |x| < 2, x ∈ ℤ};

b) {3; 6; 9} ... {x ∈ ℕ | x là ước của 18};

c) {x | x = 5k, k ∈ ℕ} ... { x ∈ ℕ | x là bội của 5};

d) {4k | k ∈ ℕ} ... {x | x = 2m, m ∈ ℕ}.

Lời giải:

a) Ta có: x(x – 1)(x + 1) = 0 ⇔ x = 0 hoặc x = 1 hoặc x = – 1.

Do đó, {x | x(x – 1)(x + 1) = 0} = {– 1; 0; 1}.         (1)

Lại có: các số nguyên x, sao cho |x| < 2 thì |x| = 0, |x| = 1 hay x = 0, x = 1, x = – 1.

Do đó, {x | |x| < 2, x ∈ ℤ} = {– 1; 0; 1}.        (2)

Từ (1) và (2) suy ra {x | x(x – 1)(x + 1) = 0} = {x | |x| < 2, x ∈ ℤ}.

b) Các số tự nhiên là ước của 18 là: 0; 2; 3; 6; 9; 18.

Do đó, {x ∈ ℕ | x là ước của 18} = {0; 2; 3; 6; 9; 18}.

Vậy {3; 6; 9} ⊂ {x ∈ ℕ | x là ước của 18}.

c) Ta có: x = 5k, k ∈ ℕ, do đó x là các số tự nhiên chia hết cho 5 hay x là bội của 5.

Do đó, {x | x = 5k, k ∈ ℕ} = { x ∈ ℕ | x là bội của 5}.

d) Tập hợp {4k | k ∈ ℕ} gồm các số tự nhiên chia hết cho 4, tập hợp {x | x = 2m, m ∈ ℕ} gồm các số tự nhiên chia hết cho 2. Một số tự nhiên chia hết cho 4 thì chia hết cho 2, nhưng một số tự nhiên chia hết cho 2 thì chưa chắc đã chia hết cho 4.

Do đó, {4k | k ∈ ℕ} ⊂ {x | x = 2m, m ∈ ℕ}.

Bài 5 trang 13 SBT Toán 10 Tập 1: Hãy chỉ ra các quan hệ bao hàm giữa các tập hợp sau và vẽ biểu đồ Ven để biểu diễn các quan hệ đó:

A = {x | x là tứ giác};

B = {x | x là hình vuông};

C = {x | x là hình chữ nhật};

D = {x | x là hình bình hành}.

Lời giải:

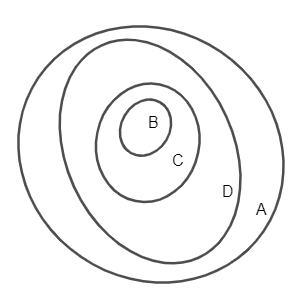
Ta có hình vuông, hình chữ nhật, hình bình hành đều là các tứ giác nên các tập hợp B, C, D đều là tập con của tập A.

Do đó ta có các quan hệ bao hàm, B ⊂ A, C ⊂ A, D ⊂ A.          (1)

Lại có hình chữ nhật là hình bình hành nên các phần tử của tập hợp C đều là phần tử của tập hợp D, do đó C ⊂ D.       (2).

Mà hình vuông là hình chữ nhật nên các phần tử của tập hợp B đều là các phần tử của tập hợp C, do đó B ⊂ C.     (3)

Từ (1), (2), (3) và theo tính chất bắc cầu, ta suy ra quan hệ bao hàm: B ⊂ C ⊂ D ⊂ A.

Ta vẽ biểu đồ Ven như sau:

Bài 6 trang 13 SBT Toán 10 Tập 1: Tìm tất cả các tập hợp A thỏa mãn điều kiện {a; b} ⊂ A ⊂ {a; b ; c; d}. 

Lời giải:

Ta có: {a; b} ⊂ A nên tập hợp {a; b} là tập con của tập hợp A, do đó các phần tử của tập {a; b} đều là phần tử của tập A hay a, b là các phần tử của tập A.

Mà A ⊂ {a; b; c; d} nên tập A là tập con của tập {a; b; c; d}, do đó các phần tử của tập A đều là các phần tử của tập {a; b; c; d}, mà tập {a; b; c; d} gồm các phần tử là a, b, c, d, trong đó có a, b là các phần tử của tập A, do đó c, d có thể là các phần tử của tập A.

Vậy ta có các tập hợp A thỏa mãn điều kiện của bài toán là:

{a; b}, {a; b; c}, {a; b; d}, {a; b; c; d}.  

Bài 7 trang 13 SBT Toán 10 Tập 1: Cho các tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7; 9}. Hãy tìm tập hợp M có nhiều phần tử nhất thỏa mãn M ⊂ A và M ⊂ B.

Lời giải:

Do M ⊂ A nên các phần tử của tập hợp M đều là các phần tử của tập A.

Do M ⊂ B nên các phần tử của tập hợp M đều là các phần tử của tập B.

Các phần tử vừa thuộc tập A vừa thuộc tập B là 1; 3; 5.

Do đó tập hợp M có nhiều phần tử nhất thỏa mãn M ⊂ A và M ⊂ B là tập hợp các phần tử vừa thuộc A vừa thuộc B.

Vậy M = {1; 3; 5}.

Bài 8 trang 13 SBT Toán 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {y ∈ ℕ | y = 10 – x², x ∈ ℕ};

b) B = $\left\{x\in \mathbb{N}|\frac{6}{6-x}\in \mathbb{N}\right\}$;

c) C = {x ∈ ℕ | 2x – 3 ≥ 0 và 7 – x ≥ 2};

d) D = {(x; y) | x ∈ ℕ, y ∈ ℕ, x + 2y = 8}. 

Lời giải:

a) Do x, y đều là các số tự nhiên nên ta lần lượt thay các giá trị x bởi các số tự nhiên 0; 1; 2; ... vào y = 10 – x² để tìm các số y thỏa mãn là số tự nhiên.

Với x = 0 thì y = 10 – 0² = 10;

Với x = 1 thì y = 10 – 1² = 9;

Với x = 2 thì y = 10 – 2² = 6;

Với x = 3 thì y = 10 – 3² = 1;

Với x = 4 thì y = 10 – 4² = – 6 ∉ ℕ, ta dừng lại.

Do đó các số tự nhiên y thỏa mãn tập A là 1; 6; 9; 10.

Vậy A = {1; 6; 9; 10}.

b) Vì $\frac{6}{6-x}\in \mathbb{N}$ nên 6 phải chia hết cho (6 – x) hay (6 – x) là ước tự nhiên của 6.

Mà các ước tự nhiên của 6 là: 1, 2, 3, 6.

Với 6 – x = 1, suy ra x = 5 ∈ ℕ nên x = 5 thỏa mãn.

Với 6 – x = 2, suy ra x = 4 ∈ ℕ nên x = 4 thỏa mãn.

Với 6 – x = 3, suy ra x = 3 ∈ ℕ nên x = 3 thỏa mãn.

Với 6 – x = 6, suy ra x = 0 ∈ ℕ nên x = 0 thỏa mãn.

Vậy B = {0; 3; 4; 5}.

c) Ta có: 2x – 3 ≥ 0 ⇔ x ≥ $\frac{3}{2}$.

Và 7 – x ≥ 2 ⇔ x ≤ 7 – 2 ⇔ x ≤ 5.

Do đó, $\frac{3}{2}$≤ x ≤ 5.

Mà x ∈ ℕ và $\frac{3}{2}=1,5$ nên x là các số tự nhiên lớn hơn hoặc bằng 2 và nhỏ hơn hoặc bằng 5, đó là 2; 3; 4; 5.

Vậy C = {2; 3; 4; 5}.

d) Ta có: x + 2y = 8 ⇔ x = 8 – 2y.

Do x ∈ ℕ, y ∈ ℕ nên ta có các trường hợp sau:

+ Với y = 0 thì x = 8 – 2 . 0 = 8

+ Với y = 1 thì x = 8 – 2 . 1 = 6

+ Với y = 2 thì x = 8 – 2 . 2 = 4

+ Với y = 3 thì x = 8 – 2 . 3 = 2

+ Với y = 4 thì x = 8 – 2 . 4 = 0

+ Với y = 5 thì x = 8 – 2 . 5 = – 2 ∉ ℕ, ta dừng lại.

Do đó ta có các cặp số (x; y) thỏa mãn là: (0; 4); (2; 3); (4; 2); (6; 1); (8; 0).

Vậy D = {(0; 4); (2; 3); (4; 2); (6; 1); (8; 0)}.

Bài 9 trang 13 SBT Toán 10 Tập 1: Cho hai tập hợp A = {2k + 1 | k ∈ ℤ} và B = {6l + 3 | l ∈ ℤ}. Chứng minh rằng B ⊂ A.

Lời giải:

Để chứng minh B ⊂ A, ta chứng minh mọi phần tử của B đều là phần tử của A.

Lấy phần tử x tùy ý của B, ta có: x = 6l + 3, l ∈ ℤ.

Ta viết: x = 2 . 3l + 2 + 1 = 2(3l + 1) + 1 = 2k + 1 với k = 3l­ + 1 ∈ ℤ.

Suy ra x ∈ A.

Vậy, với mọi x ∈ B ta đều có x ∈ A. Do đó, B ⊂ A.

Bài 10 trang 13 SBT Toán 10 Tập 1: Cho hai tập hợp A = {1; 2; a} và B = {1; a²}. Tìm tất cả các giá trị của a sao cho B ⊂ A.

Lời giải:

Ta có B ⊂ A khi mọi phần tử của tập B đều là phần tử của tập A.

Tập A có ba phần tử là 1; 2; a.

Tập B có hai phần tử là 1; a².

Do 1 ∈ A nên để B ⊂ A thì a² ∈ A hay a² = 1 hoặc a² = 2 hoặc a² = a.

Với a² = 1 thì a = 1 hoặc a = – 1.

Với a² = 2 thì a = $\sqrt{2}$ hoặc a = $-\sqrt{2}$.

Với a² = a ⇔ a² – a = 0 ⇔ a(a – 1) = 0 ⇔ a = 0 hoặc a = 1.

Vậy các giá trị của a để thỏa mãn yêu cầu là: $-\sqrt{2}$; – 1; 0; 1; $\sqrt{2}$.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Mệnh đề

Bài 3: Các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn

Lý thuyết Tập hợp

1. Nhắc lại về tập hợp

- Trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.

- Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa A, B, C, … và kí hiệu phần tử của tập hợp bằng các chữ cái in thường a, b, c, ….

Chú ý: Đôi khi, để ngắn gọn, người ta dùng từ “tập” thay cho “tập hợp”.

- Để chỉ a là một phần tử của tập hợp A, ta viết a ∈ A (đọc là “a thuộc A”). Để chỉ a không là phần tử của tập hợp A, ta viết a ∉ A (đọc là “a không thuộc A”).

Ví dụ 1.

+ Để chỉ 5 là phần tử của tập số tự nhiên ℕ, ta viết 5 ∈ ℕ.

+ Để chỉ - 1 không là phần tử của tập số tự nhiên ℕ, ta viết -1 ∉ ℕ.

- Một tập hợp có thể không chứa phần tử nào. Tập hợp như vậy gọi là tập rỗng, kí hiệu ∅.

- Người ta thường kí hiệu các tập hợp số như sau: ℕ là tập hợp các số tự nhiên, ℤ là tập hợp các số nguyên, ℚ là tập hợp các số hữu tỉ, ℝ là tập hợp các số thực.

Ví dụ 2. Muốn kí hiệu phần tử 5 thuộc tập số tự nhiên, ta kí hiệu: 5 ∈ ℕ.

*Cách xác định tập hợp

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

Chú ý: Khi liệt kê các phần tử của tập hợp, ta có một số chú ý sau đây:

+ Các phần tử có thể được viết theo thứ tự tùy ý.

+ Mỗi phần tử chỉ được liệt kê một lần.

+ Nếu quy tắc xác định các phần tử đủ rõ thì người ta dùng “…” mà không nhất thiết viết ra tất cả các phần tử của tập hợp.

- Có những tập hợp ta có thể đếm hết các phần tử của chúng. Những tập hợp như vậy được gọi là tập hợp hữu hạn.

Ví dụ 3. Cho tập hợp D các số tự nhiên chia hết cho 3 và lớn hơn 3 nhưng nhỏ hơn 10. Mô tả tập hợp D theo hai cách:

Cách 1: Liệt kê phẩn tử tập hợp: D = {6; 9}.

Cách 2: Chỉ ra tính chất đặc trưng của các phẩn tử: D = {n ∈ ℕ | n ⋮ 3, 3 < n < 10}.

2. Tập con và hai tập hợp bằng nhau

- Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A ⊂ B (đọc là A chứa trong B), hoặc B ⊃ A (đọc là B chứa A).

Nhận xét:

+ A ⊂ A và ∅ ⊂ A với mọi tập hợp A.

+ Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B (đọc là A không chứa trong B hoặc B không chứa A).

+ Nếu A ⊂ B hoặc B ⊂ A thì ta nói A và B có quan hệ bao hàm.

- Trong toán học, người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường cong kín, gọi là biểu đồ Ven.

Chú ý: Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu tỉ, tập số thực), ta có quan hệ bao hàm:  ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.

Ví dụ 4. Cho tập hợp T = {2; 3; 5}; S = {2; 3; 5; 7; 9}; M = {2; 3; 4; 5}.

+ Tập hợp T là tập con của tập hợp S vì tất cả phần tử của T đều có trong phần tử của S.

+ Tập hợp M không là tập hợp con của tập hợp S vì tập M có phần tử 4 không thuộc S.

- Hai tập hợp A và B được gọi là bằng nhau, kí hiệu A = B, nếu A ⊂ B và B ⊂ A.

Ví dụ 5. Cho 2 tập hợp: T = {n ∈ ℕ | n ⋮ 9, 7 < n < 14} và S = {n ∈ ℕ | n ⋮ 3, 8 < n < 10}.

Tìm các phần tử của T và S ta có T = {9} và S = {9} nên T = S.

3. Một số tập con của tập hợp số thực

- Ta thường sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a < b):

Tên gọi và kí hiệu	Tập hợp	Biểu diễn trên trục số
Tập số thực (-∞; +∞)	ℝ
Đoạn [a; b]	{x ∈ ℝ | a ≤  x ≤ b}
Khoảng (a; b)	{x ∈ ℝ | a < x < b}
Nửa khoảng [a; b)	{x ∈ ℝ | a ≤  x < b}
Nửa khoảng (a; b]	{x ∈ ℝ | a < x ≤ b}
Nửa khoảng (-∞; a]	{x ∈ ℝ |  x ≤ a}
Nửa khoảng [a; +∞)	{x ∈ ℝ | x ≥ a}
Khoảng (-∞; a)	{x ∈ ℝ | x < a}
Khoảng (a; +∞)	{x ∈ ℝ | x > a}

- Trong các kí hiệu trên, kí hiệu - ∞ đọc là âm vô cực (âm vô cùng), kí hiệu + ∞ đọc là dương vô cực (dương vô cùng).

Ví dụ 6.

Cho x thỏa mãn 2 < x ≤ 6 thì ta kí hiệu x ∈ (2; 6].

Cho x thỏa mãn x ≥ 7 thì ta kí hiệu x ∈ [7; +∞).