Với lời giải SBT Toán 10 trang 58 Tập 1 chi tiết trong Bài 10: Vectơ trong mặt phẳng tọa độ sách Kết nối tri thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 4.22 trang 58 SBT Toán 10 Tập 1:

Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

Lời giải:

Cách 1:

Gọi A(x_A; y_A); B(x_B; y_B) và C(x_C; y_C) là tọa độ ba đỉnh của tam giác ABC.

Ta có:

+) M(4; 0) là trung điểm của BC nên $\left\{\begin{array}{l}4=\frac{x_B+x_C}{2}\\ 0=\frac{y_B+y_C}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_B+x_C=8\\ y_B+y_C=0\end{array}\right.$                                 (1)

+) N(5; 2) là trung điểm của CA nên $\left\{\begin{array}{l}5=\frac{x_A+x_C}{2}\\ 2=\frac{y_A+y_C}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_A+x_C=10\\ y_A+y_C=4\end{array}\right.\iff \left\{\begin{array}{l}{x}_C=10-x_A\\ y_C=4-y_A\end{array}\right.$     (2)

+) P(2; 3) là trung điểm của AB nên $\left\{\begin{array}{l}2=\frac{x_A+x_B}{2}\\ 3=\frac{y_A+y_B}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_A+x_B=4\\ y_A+y_B=6\end{array}\right.\iff \left\{\begin{array}{l}{x}_B=4-x_A\\ y_B=6-y_A\end{array}\right.$        (3)

Thay (2) và (3) vào (1) ta được:

$\left\{\begin{array}{l}\left(4-x_A\right)+\left(10-x_A\right)=8\\ \left(6-y_A\right)+\left(4-y_A\right)=0\end{array}\right.$$\iff \left\{\begin{array}{l}14-2x_A=8\\ 10-2y_A=0\end{array}\right.$

$\iff \left\{\begin{array}{l}{x}_A=3\\ y_A=5\end{array}\right.$ Þ A(3; 5)

Khi đó $\left\{\begin{array}{l}{x}_B=4-3=1\\ y_B=6-5=1\end{array}\right.$ Þ B(1; 1)

$\left\{\begin{array}{l}{x}_C=10-3=7\\ y_C=4-5=-1\end{array}\right.$Þ C(7; –1)

Vậy A(3; 5), B(1; 1) và C(7; –1).

Cách 2:

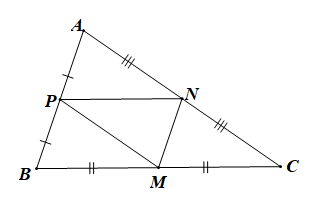
Do M, N, P lần lượt là trung điểm của BC, CA, AB

Nên MN, NP, PM là các đường trung bình của tam giác ABC.

Þ MN // AB, NP // BC, MP // AC.

+) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành

$\Rightarrow \overrightarrow{MB}=\overrightarrow{NP}$

Gọi B(x_B; y_B) và có M(4; 0), N(5; 2) và P(2, 3).

$\Rightarrow \overrightarrow{MB}=\left(x_B-4;y_B\right)$ và $\overrightarrow{NP}=\left(2-5;3-2\right)=\left(-3;1\right)$

Khi đó $\overrightarrow{MB}=\overrightarrow{NP}\iff \left\{\begin{array}{l}{x}_B-4=-3\\ y_B=1\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_B=1\\ y_B=1\end{array}\right.$ Þ B(1; 1)

Tương tự ta cũng có A(3; 5) và C(7; –1).

Vậy A(3; 5), B(1; 1) và C(7; –1).

Bài 4.23 trang 58 SBT Toán 10 Tập 1:

Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0).

a) Tính độ dài các đoạn thẳng AB, BC và CA. Từ đó suy ra tam giác ABC là một tam giác vuông cân.

b) Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.

Lời giải:

a) Với A(2;–1), B(1; 4) và C(7; 0) ta có:

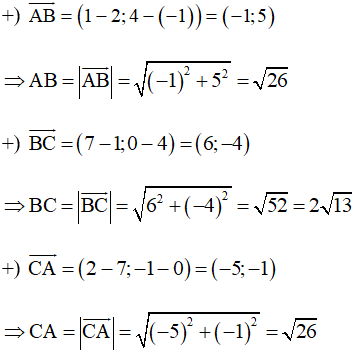
Do đó AB = CA $\left(=\sqrt{26}\right)$

Nên tam giác ABC cân tại A               (1)

Mặt khác: $B{C}^2={\left(2\sqrt{13}\right)}^2=52$

Và $A{B}^2+A{C}^2={\left(\sqrt{26}\right)}^2+{\left(\sqrt{26}\right)}^2=52$

Þ BC² = AB² + AC²

Theo định lí Pythagoras đảo thì tam giác ABC vuông tại A        (2)

Từ (1) và (2) suy ra tam giác ABC vuông cân tại A với $AB=AC=\sqrt{26};BC=2\sqrt{13}.$

b)

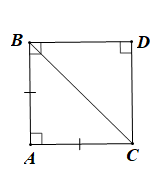
Vì ABC là tam giác vuông cân

Nên để ABDC là hình vuông thì tứ giác ABDC là hình bình hành

$\iff \overrightarrow{CA}=\overrightarrow{DB}$

Gọi D(x_D; y_D) và có A(2;–1), B(1; 4), C(7; 0).

$\Rightarrow \overrightarrow{CA}=\left(-5;-1\right)$và $\overrightarrow{DB}=\left(1-x_D;4-y_D\right)$

Do đó $\overrightarrow{CA}=\overrightarrow{DB}\iff \left\{\begin{array}{l}-5=1-x_D\\ -1=4-y_D\end{array}\right.$

$\iff \left\{\begin{array}{l}{x}_D=6\\ y_D=5\end{array}\right.$ Þ D(6; 5).

Vậy tọa độ điểm D cần tìm là D(6; 5).

Bài 4.24 trang 58 SBT Toán 10 Tập 1:

Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).

a) Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.

b) Tìm toạ độ của điểm Q sao cho $\overrightarrow{MQ}=2\overrightarrow{PN}.$

c) Tìm toạ độ của điểm R thoả mãn $\overrightarrow{RM}+2\overrightarrow{RN}=\overrightarrow{0}.$ Từ đó suy ra P, Q, R thẳng hàng.

Lời giải:

a) Gọi P(a; 0) là điểm thuộc tia Ox.

Với M(–2; 1) và N(4; 5) ta có:

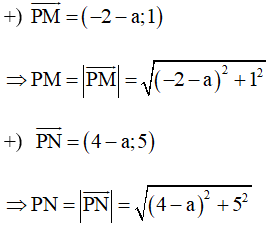
 Do đó PM = PN $\iff \sqrt{{\left(-2-a\right)}^2+1^2}=\sqrt{{\left(4-a\right)}^2+5^2}$

Û (–2 – a)² + 1² = (4 – a)² + 5²

Û 4 + 4a + a² + 1 = 16 – 8a + a² + 25

Û 12a = 36

Û a = 3.

Vậy P(3; 0).

b) Giả sử điểm Q có tọa độ là Q(x; y).

Với M(–2; 1), N(4; 5) và P(3; 0) ta có:

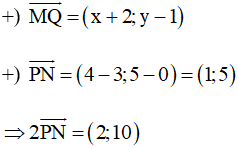
Do đó $\overrightarrow{MQ}=2\overrightarrow{PN}\iff \left\{\begin{array}{l}x+2=2\\ y-1=10\end{array}\right.$

$\iff \left\{\begin{array}{l}x=0\\ y=11\end{array}\right.$ Þ Q(0; 11).

Vậy Q(0; 11).

c) Giả sử R(x₀; y₀) là điểm cần tìm.

Với M(–2; 1) và N(4; 5) ta có:

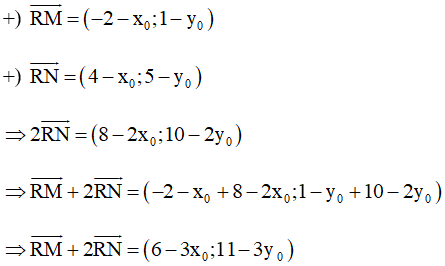
Do đó 

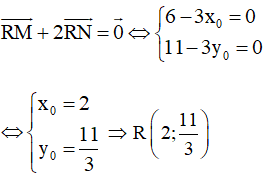
+) Ta xét ba điểm: P(3; 0), Q(0; 11) và $R\left(2;\frac{11}{3}\right)$

$\Rightarrow \overrightarrow{PQ}=\left(-3;11\right)$và $\overrightarrow{QR}=\left(2;\frac{11}{3}-11\right)=\left(2;\frac{-22}{3}\right)$

Có: $\frac{-3}{2}=\frac{11}{\frac{-22}{3}}$ nên hai vectơ $\overrightarrow{PQ}$ và $\overrightarrow{QR}$ cùng phương

Do đó P, Q, R thẳng hàng

Vậy ba điểm P, Q, R thẳng hàng.

Xem thêm các bài giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải SBT Toán 10 trang 59, 60 Tập 1

Giải SBT Toán 10 trang 61, 62 Tập 1

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số