Với giải sách bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0° đến 180° sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 5: Giá trị lượng giác của một góc từ 0° đến 180°

Giải SBT Toán 10 trang 32 Tập 1

Bài 3.1 trang 32 SBT Toán 10 Tập 1: Tính giá trị của biểu thức:

a) A = sin45° + 2sin60° + tan120° + cos135°;

b) B = tan45° . cot135° - sin30° . cos120° - sin60° . cos150°;

c) C = cos²5° + cos²25° + cos²45° + cos²65° + cos²85°;

d) D = $\frac{12}{1+{\tan }^{2}73°}$ - 4tan75° . cot105° +  12sin²107° - 2tan40° . cos60° . tan50°;

e) E = 4tan32° . cos60° . cot148° + $\frac{5{\cot }^{2}108°}{1+{\tan }^{2}18°}$ + 5sin²72°.

Lời giải:

a) A = sin45° + 2sin60° + tan120° + cos135°

Ta có sin 45° = $\frac{1}{\sqrt{2}}$; sin 60° = $\frac{\sqrt{3}}{2}$;

tan 120° = $-\sqrt{3}$; cos 135° = $-\frac{1}{\sqrt{2}}$.

Khi đó A = $\frac{1}{\sqrt{2}}+2.\frac{\sqrt{3}}{2}+\left(-\sqrt{3}\right)+\left(-\frac{1}{\sqrt{2}}\right)$

= $\frac{1}{\sqrt{2}}+\sqrt{3}-\sqrt{3}-\frac{1}{\sqrt{2}}$

= 0.

Vậy A = 0.

b) B = tan45° . cot135° - sin30° . cos120° - sin60° . cos150°

Ta có tan45° = 1; cot135° = -1;

sin30° = $\frac{1}{2}$; cos120° = $\frac{-1}{2}$;

sin60° = $\frac{\sqrt{3}}{2}$; cos150° = $-\frac{\sqrt{3}}{2}$.

Khi đó B = 1 . (-1) - $\frac{1}{2}.\left(-\frac{1}{2}\right)$ - $\frac{\sqrt{3}}{2}.\left(-\frac{\sqrt{3}}{2}\right)$

= -1 + $\frac{1}{4}$ + $\frac{3}{4}$ = 0.

Vậy B = 0.

c) C = cos²5° + cos²25° + cos²45° + cos²65° + cos²85°

Ta có cos45° = $\frac{1}{\sqrt{2}}$;

cos5° = cos(90° - 85°) = sin85°;

cos25° = cos(90° - 65°) = sin65°.

Do đó: cos²5° = sin²85°; cos²25° = sin²65°.

Khi đó C = sin²85° + sin²65° + $\frac{1}{2}$ + cos²65° + cos²85°

C = (sin²85° + cos²85°) + (sin²65° + cos²65°) + $\frac{1}{2}$

= 1 + 1 + $\frac{1}{2}$ = $\frac{5}{2}$.

Vậy C = $\frac{5}{2}$.

d) D = $\frac{12}{1+{\tan }^{2}73°}$ - 4tan75° . cot105° +  12sin²107° - 2tan40° . cos60° . tan50°

Ta có 1 + tan²73° = 1 + $\frac{{\sin }^{2}73°}{{\cos }^{2}73°}$

= $\frac{{\cos }^{2}73°}{{\cos }^{2}73°}+\frac{{\sin }^{2}73°}{{\cos }^{2}73°}$

= $\frac{{\cos }^{2}73°+{\sin }^{2}73°}{{\cos }^{2}73°}$ = $\frac{1}{{\cos }^{2}73°}$ 

=> $\frac{1}{1+{\tan }^{2}73°}$ = cos²73°

=> $\frac{12}{1+{\tan }^{2}73°}$ = 12cos²73°

Khi đó:

D = 12cos²73° - 4 . tan(180° - 105°) . cot105° + 12sin²107° - 2tan(90° - 50°) . cos60° . tan50°

= 12cos²73° – 4(–tan105°) . cot105° + 12sin² 107° - 2cot50° . cos60° . tan50°

= 12cos² 73° + 12sin² 73° + 4tan105° . cot105° - 2cot 50° . tan 50° . cos 60°

= 12(cos² 73° + sin² 73°) + 4.1 – 2.1.cos60°

= 12 + 4 - 2. $\frac{1}{2}$ = 15.

Vậy D = 15.

e) E = 4tan32° . cos60° . cot148° + $\frac{5{\cot }^{2}108°}{1+{\tan }^{2}18°}$ + 5sin²72°

Ta có 1 + tan² 18° = 1 + $\frac{{\sin }^{2}18°}{{\cos }^{2}18°}$ 

= $\frac{{\cos }^{2}18°}{{\cos }^{2}18°}+\frac{{\sin }^{2}18°}{{\cos }^{2}18°}$ 

= $\frac{{\cos }^{2}18°+{\sin }^{2}18°}{{\cos }^{2}18°}$ 

= $\frac{1}{{\cos }^{2}18°}$

Þ $\frac{5{\cot }^{2}108°}{1+{\tan }^{2}108°}$ = 5cot²108° . cos²18°

= 5[cot(180° - 72°)]² . cos²18°

= 5.(-cot72°)² . cos²18°

= 5.cot²72° . cos²18°

Khi đó:

E = 4tan32° . cos60° . cot(180° - 32°) + 5cot² 72° . cos²18° + 5[sin(90° - 18°)]²

= 4tan32° . cos60° . (-cot32°) + 5 cot²72° . cos²18° + 5cos²18°

= -4cos60° + 5cos²18° . (cot²72° + 1)

= -4 . $\frac{1}{2}$ + 5cos²18° . $\frac{1}{{\sin }^{2}72°}$

= -2 + 5cos²18° . $\frac{1}{{\left[\sin \left(90°-18°\right)\right]}^2}$

= -2 + 5cos² 18° . $\frac{1}{{\cos }^{2}18°}$

= -2 + 5 = 3.

Vậy E = 3.

Bài 3.2 trang 32 SBT Toán 10 Tập 1: Cho góc α, 90° < α < 180° thỏa mãn sin α = $\frac{3}{4}$. Tính giá trị của biểu thức:

$F=\frac{\tan \alpha +2\cot \alpha }{\tan \alpha +\cot \alpha }$.

Lời giải:

Do 90° < α < 180° nên sinα > 0, cosα < 0.

Ta có sin² α + cos² α = 1.

Þ cos² α = 1 - sin² α

Þ cos² α = 1 - ${\left(\frac{3}{4}\right)}^2$ = 1 - $\frac{9}{16}$ = $\frac{7}{16}$.

Mà cos α < 0 nên cos α = $-\sqrt{\frac{7}{16}}$ = $\frac{-\sqrt{7}}{4}$.

Khi đó:

• tan α = $\frac{\sin \alpha }{\cos \alpha }=\frac{3}{4}:\frac{-\sqrt{7}}{4}=\frac{3}{4}.\frac{4}{-\sqrt{7}}=\frac{-3}{\sqrt{7}}$.

• cot α = 1 : tan α = $\frac{-\sqrt{7}}{3}$.

Khi đó F = $\frac{\frac{-3}{\sqrt{7}}+2.\frac{-\sqrt{7}}{3}}{\frac{-3}{\sqrt{7}}+\frac{-\sqrt{7}}{3}}$ 

= $\frac{\frac{-3}{\sqrt{7}}-\frac{2\sqrt{7}}{3}}{\frac{-3}{\sqrt{7}}-\frac{\sqrt{7}}{3}}=\frac{\frac{-9-14}{3\sqrt{7}}}{\frac{-9-7}{3\sqrt{7}}}$ 

= $\frac{-23}{3\sqrt{7}}:\frac{-16}{3\sqrt{7}}$ = $\frac{23}{16}$

Vậy F = $\frac{23}{16}$.

Giải SBT Toán 10 trang 33 Tập 1

Bài 3.3 trang 33 SBT Toán 10 Tập 1: Cho góc α thỏa mãn 0° < α < 180°, tanα = 2. Tính giá trị của các biểu thức sau:

a) G = 2sin α + cos α;

b) H = $\frac{2\sin \alpha +\cos \alpha }{\sin \alpha -\cos \alpha }$.

Lời giải:

Do 0° < α < 180° nên sinα > 0.

Mà tanα = $\frac{\sin \alpha }{\cos \alpha }$ = 2 > 0 nên sin α và cos α cùng dấu, do đó cosα > 0.

Do tanα = $\frac{\sin \alpha }{\cos \alpha }$ = 2 nên sinα = 2cosα

=> sin²α = 4cos²α

Ta có sin²α + cos²α = 1

=> 4cos α + cos²α = 1

=> 5cos²α = 1

=> cos²α = $\frac{1}{5}$

Do cosα > 0 nên cosα = $\frac{1}{\sqrt{5}}$.

Do đó sinα = $\frac{2}{\sqrt{5}}$.

a) G = 2sinα + cosα

= 2 . $\frac{2}{\sqrt{5}}$ + $\frac{1}{\sqrt{5}}$

= $\frac{4}{\sqrt{5}}+\frac{1}{\sqrt{5}}$

= $\frac{5}{\sqrt{5}}$= $\sqrt{5}$

Vậy G = $\sqrt{5}$.

b) H = $\frac{2\sin \alpha +\cos \alpha }{\sin \alpha -\cos \alpha }$

= $\frac{2.\frac{2}{\sqrt{5}}+\frac{1}{\sqrt{5}}}{\frac{2}{\sqrt{5}}-\frac{1}{\sqrt{5}}}$ = $\frac{\frac{4}{\sqrt{5}}+\frac{1}{\sqrt{5}}}{\frac{1}{\sqrt{5}}}$

= $\frac{5}{\sqrt{5}}.\sqrt{5}$ = 5

Vậy H = 5.

Bài 3.4 trang 33 SBT Toán 10 Tập 1: Cho góc α thỏa mãn 0° < α < 180°, tanα = $\sqrt{2}$. Tính giá trị của biểu thức

K = $\frac{{\sin }^3\alpha +\sin \alpha .{\cos }^2\alpha +2{\sin }^2\alpha .\cos \alpha -4{\cos }^3\alpha }{\sin \alpha -\cos \alpha }$.

Lời giải:

Do 0° < α < 180° nên sinα > 0.

Mà tanα = $\frac{\sin \alpha }{\cos \alpha }$ = $\sqrt{2}$ > 0 nên sinα và cosα cùng dấu, do đó cosα > 0.

Chia cả tử và mẫu của K cho cos³α ta được:

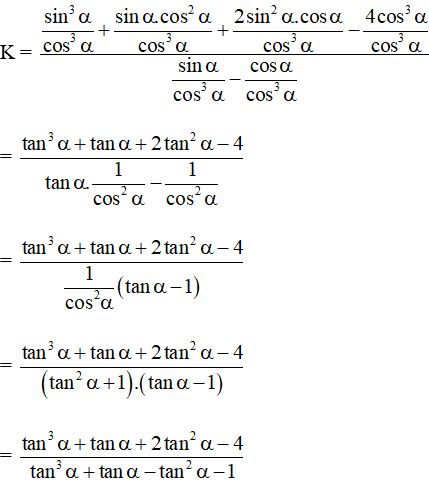
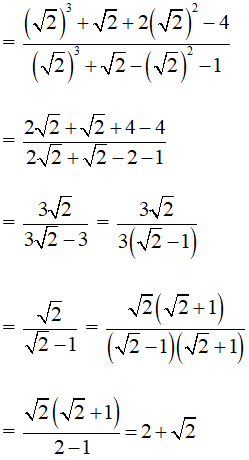
Vậy K = 2 + $\sqrt{2}$

Bài 3.5 trang 33 SBT Toán 10 Tập 1: Chứng minh rằng:

a) sin⁴α + cos⁴α = 1 - 2sin²α . cos²α;

b) sin⁶α + cos⁶α = 1 - 3sin²α . cos²α;

c*) $\sqrt{{\sin }^4\alpha +6{\cos }^2\alpha +3}+$$\sqrt{{\cos }^4\alpha +4{\sin }^2\alpha }=4$.

Lời giải:

a) Ta có (sin²α + cos²α)² = sin⁴α + 2sin²α . cos²α + cos⁴α

=> 1² = sin⁴α + cos⁴α + 2sin²α . cos²α

=> sin⁴α + cos⁴α = 1 - 2sin²α . cos²α

Vậy sin⁴α + cos⁴α = 1 - 2sin²α . cos²α.

b) Ta có (sin²α + cos²α)³ = sin⁶α + cos⁶α + 3sin²α . cos²α(sin²α + cos²α)

=> 1³ = sin⁶α + cos⁶α + 3sin²α . cos²α . 1

=> sin⁶α + cos⁶α = 1 - 3sin²α . cos²α

Vậy sin⁶α + cos⁶α = 1 - 3sin²α . cos²α.

c) Xét sin⁴α + 6cos²α + 3

= sin⁴α + 6(1 - sin²α) + 3

= sin⁴α - 6sin²α + 9

= (sin²α - 3)²

=> $\sqrt{{\sin }^4\alpha +6{\cos }^2\alpha +3}=\sqrt{{\left({\sin }^2\alpha -3\right)}^2}$

= |sin²α – 3| = 3 - sin²α

(do 0 ≤ sin²α < 1 nên sin²α – 3 < 0).

Xét cos⁴α + 4sin²α

= cos⁴α + 4(1 - cos²α)

= cos⁴α - 4 cos²α + 4

= (cos²α - 2)²

=> $\sqrt{{\cos }^4\alpha +4{\sin }^2\alpha }=\sqrt{{\left({\cos }^2\alpha -2\right)}^2}$

 = |cos²α – 2| = 2 - cos²α

(do 0 ≤ cos²α < 1 nên cos²α – 2 < 0).

=> $\sqrt{{\sin }^4\alpha +6{\cos }^2\alpha +3}+$$\sqrt{{\cos }^4\alpha +4{\sin }^2\alpha }$ 

= 3 - sin² α + 2 - cos² α

= 5 - (sin² α + cos² α)

= 5 - 1

= 4.

Vậy $\sqrt{{\sin }^4\alpha +6{\cos }^2\alpha +3}+$$\sqrt{{\cos }^4\alpha +4{\sin }^2\alpha }=4$.

Bài 3.6 trang 33 SBT Toán 10 Tập 1: Góc nghiêng của Mặt Trời tại một vị trí trên Trái Đất là góc nghiêng giữa tia nắng lúc giữa trưa với mặt đất. Trong thực tế, để đo trực tiếp góc này, vào giữa trưa (khoảng 12 giờ), em có thể dựng một thước thẳng vuông góc với mặt đất, đo độ dài của bóng thước trên mặt đất. Khi đó, tang của góc nghiêng Mặt Trời tại vị trí đặt thước bằng tỉ số giữa độ dài của thước và độ dài của bóng thước. Góc nghiêng của Mặt Trời phụ thuộc vào vĩ độ của vị trí đo và phụ thuộc vào thời gian đo trong năm (ngày thứ mấy trong năm). Tại vị trí có vĩ độ f và ngày thứ N trong năm, góc nghiêng của Mặt Trời α còn được tính theo công thức sau:

α = 90° - f - $\left|\cos \left(\left(\frac{2\left(N+10\right)}{365}-m\right)180°\right)\right|$ . 23,5°

trong đó m = 0 nếu 1 ≤ N ≤ 172, m = 1 nếu 173 ≤ N ≤ 355, m = 2 nếu 356 ≤ N ≤ 365.

a) Hãy áp dụng công thức trên để tính góc nghiêng của Mặt Trời vào ngày 10/10 trong năm không nhuận (năm mà tháng 2 có 28 ngày) tại vị trí có vĩ độ f = 20°.

b) Hãy xác định vĩ độ tại nơi em sinh sống và tính góc nghiêng của Mặt Trời tại đó theo hai cách đã được đề cập trong bài toán (đo trực tiếp và tính theo công thức) và so sánh hai kết quả thu được.

Lời giải:

a) Tháng 10 và tháng 12 có 31 ngày; tháng 11 có 30 ngày.

Nên từ 10/10 đến hết tháng 10 còn 21 ngày.

Do đó ngày 10/10 trong năm không nhuận là ngày thứ: 365 - 21 - 30 - 31 = 283 trong năm đó.

Vì 173 ≤ N = 283 ≤ 355 nên m = 1.

Góc nghiêng của Mặt Trời vào ngày 10/10 tại vị trí có vĩ độ f = 20° là:

90° - 20° - $\left|\cos \left(\left(\frac{2\left(283+10\right)}{365}-1\right)180°\right)\right|$ . 23,5°

≈ 70° - |cos109°| . 23,5°

≈ 70° - 7,65°

≈ 62,35°

Vậy góc nghiêng của Mặt Trời vào ngày 10/10 tại vị trí có vĩ độ f = 20° khoảng 62,35°.

b) Học sinh tự thực hiện việc đo và tính theo công thức để so sánh.

Lưu ý tại vị trí có vĩ độ f và ngày thứ N trong năm, góc nghiêng của Mặt Trời α còn được tính theo công thức sau:

α = 90° - f - $\left|\cos \left(\left(\frac{2\left(N+10\right)}{365}-m\right)180°\right)\right|$ . 23,5°

trong đó m = 0 nếu 1 ≤ N ≤ 172, m = 1 nếu 173 ≤ N ≤ 355, m = 2 nếu 356 ≤ N ≤ 365.

Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 2

Bài 6: Hệ thức lượng trong tam giác

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180

1. Giá trị lượng giác của một góc

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.

Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x₀; y₀) trên nửa đường tròn đơn vị để $\widehat{\mathrm{xOM}}=\mathrm{\alpha }$.

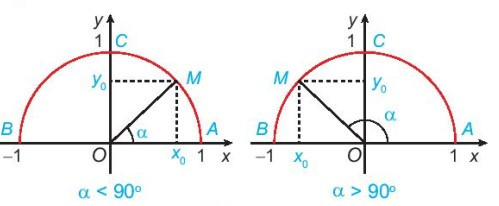
- Định nghĩa tỉ số lượng giác của một góc từ 0^o đến 180^o

Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x₀; y₀) là điểm trên nửa đường tròn đơn vị sao cho  $\widehat{\mathrm{xOM}}=\mathrm{\alpha }$. Khi đó:

+ sin của góc α là tung độ y₀ của điểm M, được kí hiệu là sin α;

+ côsin của góc α là hoành độ x₀ của điểm M, được kí hiệu là cos α;

+ Khi α ≠ 90° (hay x₀ ≠ 0), tang của α là $\frac{{\mathrm{y}}_0}{{\mathrm{x}}_0}$, được kí hiệu là tan α;

+ Khi α ≠ 0° và α ≠ 180° (hay y₀ ≠ 0), côtang của α là $\frac{{\mathrm{x}}_0}{{\mathrm{y}}_0}$, được kí hiệu là cot α.

- Từ định nghĩa trên ta có:

$\mathrm{tan\alpha }=\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}(\mathrm{\alpha }\ne 90°);$$\mathrm{cot\alpha }=\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}(\mathrm{\alpha }\ne 0°\mathrm{và}\mathrm{\alpha }\ne 180°);$$\mathrm{tan\alpha }=\frac{1}{\mathrm{cot\alpha }}\text{ (}\mathrm{\alpha }\notin \text{{}0°;90°;180°\text{}})$

- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:

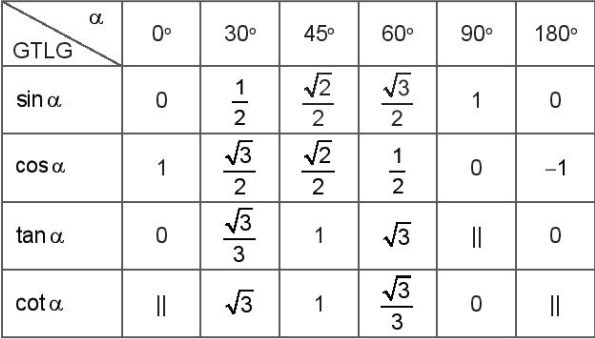
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Ví dụ: Tìm các giá trị lượng giác của góc 120°.

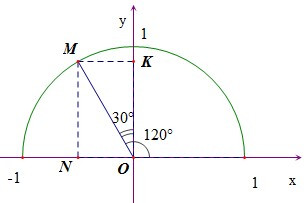
Gọi M là điểm trên nửa đường tròn đơn vị sao cho $\widehat{\mathrm{xOM}}={120}^{\mathrm{o}}$. Gọi N, K tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Do $\widehat{\mathrm{xOM}}={120}^{\mathrm{o}}$ và $\widehat{\mathrm{xOK}}={90}^{\mathrm{o}}$nên $\widehat{\mathrm{KOM}}={30}^{\mathrm{o}}$và $\widehat{\mathrm{MON}}={60}^{\mathrm{o}}$.

Từ bảng GTLG của một số góc đặc biệt:

Ta có: cos 60^o = $\frac{1}{2}$ và cos 30^o = $\frac{\sqrt{3}}{2}$

Các tam giác MOK và MON là các tam giác vuông với cạnh huyền bằng 1

Suy ra ON = cos$\widehat{\mathrm{MON}}$.OM = cos60^o.1 = $\frac{1}{2}$ và OK = cos$\widehat{\mathrm{MOK}}$.OM = cos30^o.1 = $\frac{\sqrt{3}}{2}$

Mặt khác, do điểm M nằm bên trái trục tung nên $\mathrm{M}\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$

Theo định nghĩa giá trị lượng giác ta có:

sin 120^o = $\frac{\sqrt{3}}{2}$

cos 120^o =  $-\frac{1}{2}$

tan 120^o = $\frac{\sin {120}^{\mathrm{o}}}{\cos {120}^{\mathrm{o}}}=-\sqrt{3}$

cot 120^o = $\frac{\cos {120}^{\mathrm{o}}}{\sin {120}^{\mathrm{o}}}=-\frac{1}{\sqrt{3}}$.

Vậy sin 120^o = $\frac{\sqrt{3}}{2}$; cos 120^o =  $-\frac{1}{2}$; tan 120^o = $-\sqrt{3}$; cot 120^o = $-\frac{1}{\sqrt{3}}$.

- Ta có thể dùng máy tính bỏ túi để tính giá trị gần đúng của các giá trị lượng giác của một góc.

Ví dụ:

- Ta cũng có thể tìm được góc khi biết một giá trị lượng giác của góc đó.

Ví dụ:

Chú ý:

+ Khi tìm x biết sin x, máy tính chỉ đưa ra giá trị x ≤ 90°.

+ Muốn tìm x khi biết cos x, tan x, ta cũng làm tương tự như trên, chỉ thay phím  tương ứng bởi phím .

2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Đối với hai góc bù nhau, α và 180° – α, ta có:

sin (180° – α) = sin α;

cos (180° – α) = – cos α;

tan (180° – α) = – tan α  (α ≠ 90°);

cot (180° – α) = – cot α  (0° < α < 180°).

Chú ý:

- Hai góc bù nhau có sin bằng nhau; có côsin, tang, côtang đối nhau.

Ví dụ: Tính các giá trị lượng giác của góc 135°.

Hướng dẫn giải

Ta có 135° + 45° = 180°, vì vậy góc 135° và góc 45° là hai góc bù nhau:

Suy ra:

sin135° = sin45° = $\frac{\sqrt{2}}{2}$

cos135° = – cos45° = $-\frac{\sqrt{2}}{2}$

tan135° = – tan45° = –1

cot135° = – cot45° = –1

Vậy sin135° = $\frac{\sqrt{2}}{2}$; cos135° = $-\frac{\sqrt{2}}{2}$; tan135° = –1 ; cot135° = –1.

- Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Ví dụ:

Ta có  30° + 60° = 90° nên góc 30° và góc 60° là hai góc phụ nhau.

Khi đó:  

sin30° = cos60° = $\frac{1}{2}$

tan30° = cot60° = $\frac{\sqrt{3}}{3}$.