Với giải sách bài tập Toán 7 Bài 5: Tỉ lệ thức sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 5: Tỉ lệ thức
a) Tính tỉ số giữa khối lượng thóc xay lần thứ nhất và khối lượng thóc xay lần thứ hai; tỉ số giữa khối lượng gạo xay lần thứ nhất và khối lượng gạo xay lần thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức không?
Lời giải:
a) Tỉ số giữa khối lượng thóc xay lần thứ nhất và khối lượng thóc xay lần thứ hai là:
.
Tỉ số giữa khối lượng gạo xay lần thứ nhất và khối lượng gạo xay lần thứ hai là:
.
b) Do 100 : 3 = 65 : 19,5 (cùng bằng ) nên hai tỉ số trên lập được tỉ lệ thức.
a) Tính tỉ số giữa thể tích dầu của thùng thứ nhất và thể tích dầu của thùng thứ hai; tỉ số giữa khối lượng dầu của thùng thứ nhất và khối lượng dầu của thùng thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức không?
Lời giải:
a) Tỉ số giữa thể tích dầu của thùng thứ nhất và thể tích dầu của thùng thứ hai là:
.
Tỉ số giữa khối lượng dầu của thùng thứ nhất và khối lượng dầu của thùng thứ hai là:
.
b) Do 17 : 13,6 = 15 : 12 (cùng bằng ) nên hai tỉ số trên lập được tỉ lệ thức.
Bài 40 trang 53 Toán 7 Tập 1: Từ các tỉ số sau đây có thể lập được tỉ lệ thức không?
a) 16 : 6 và 40 : 15;
b) và 12 : (−3);
c) (−39) : 2,4 và 5,85 : (−3,6);
d) và .
Lời giải:
a) Ta có: ; .
Ta thấy hai tỉ số đã cho bằng nhau và đều bằng .
Vậy ta có tỉ lệ thức 16 : 6 = 40 : 15.
b) Ta có: ; 12 : (−3) = −4.
Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
c) Ta có: ;
.
Ta thấy hai tỉ số đã cho bằng nhau và đều bằng .
Vậy ta có tỉ lệ thức (−39) : 2,4 = 5,85 : (−3,6).
d) Ta có: ; .
Ta thấy hai tỉ số đã cho bằng nhau và đều bằng .
Vậy ta có tỉ lệ thức = .
Bài 41 trang 54 Toán 7 Tập 1: Tìm số x trong mỗi tỉ lệ thức sau:
a) ;
b) ;
c) ;
d*) .
Lời giải:
a)
x = 14.
Vậy x = 14.
b)
.
Vậy .
c)
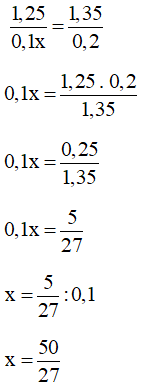
Vậy .
d*)
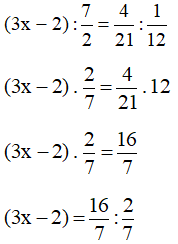
3x – 2 = 8
3x = 10
.
Vậy .
Bài 42 trang 54 Toán 7 Tập 1: Chọn số thích hợp cho :
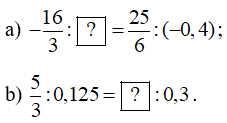
Lời giải:
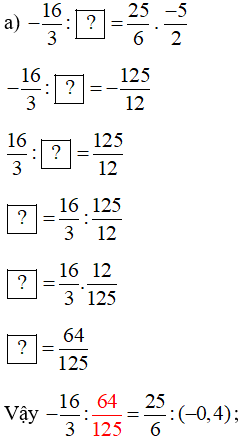
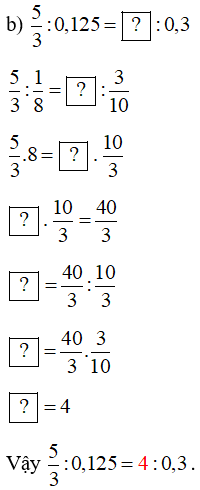
Bài 43 trang 54 Toán 7 Tập 1: Lập tất cả các tỉ lệ thức có thể có được từ bốn số sau:
a) 12; 21; 84; 3;
b) 0,36; 4,25; 0,9; 1,7;
c) ; 6; ; 8;
d) 2,5; −5,12; −3,2; 4.
Lời giải:
a) Ta có: 12 . 21 = 252; 84 . 3 = 252.
Vì 12 . 21 = 84 . 3 nên tất cả các tỉ lệ thức có thể lập được từ bốn số 12; 21; 84; 3 là:
.
b) Ta có: 0,36 . 4,25 = 1,53; 0,9 . 1,7 = 1,53.
Vì 0,36 . 4,25 = 0,9 . 1,7 nên tất cả các tỉ lệ thức có thể lập được từ bốn số 0,36; 4,25; 0,9; 1,7 là:
.
c) Ta có: ; .
Vì nên tất cả các tỉ lệ thức có thể lập được từ bốn số ; 6; ; 8 là:
d) Ta có: 2,5 . (−5,12) = −12,8; (−3,2) . 4 = −12,8.
Vì 2,5 . (−5,12) = (−3,2) . 4 nên tất cả các tỉ lệ thức có thể lập được từ bốn số 2,5; −5,12; −3,2; 4 là:
Bài 44 trang 54 Toán 7 Tập 1: Chọn ba số 6, 8, 24.
a) Tìm số x sao cho x cùng với ba số trên lập thành một tỉ lệ thức.
b) Lập tất cả tỉ lệ thức có thể có được.
Lời giải:
a) Trong ba số 6, 8, 24 có ba cách chọn ra tích của hai trong ba số đó.
• Do 6 . 8 = 48 và 48 = 24 . 2 nên x = 2.
• Do 6 . 24 = 144 và 144 = 8 . 18 nên x = 18.
• Do 8 . 24 = 192 và 192 = 6 . 32 nên x = 32.
b) Với đẳng thức 6 . 8 = 24 . 2, ta có các tỉ lệ thức sau:
.
Với đẳng thức 6 . 24 = 8 . 18, ta có các tỉ lệ thức sau:
.
Với đẳng thức 8 . 24 = 6 . 32, ta có các tỉ lệ thức sau:
.
Bài 45 trang 54 Toán 7 Tập 1: Cho tỉ lệ thức và xy = 56. Tìm x và y.
Lời giải:
Đặt .
Khi đó, ta có: x = 2k; y = 7k.
Do xy = 56 nên 2k . 7k = 56 hay 14k2 = 56 suy ra k2 = 4.
Ta thấy: 22 = (−2)2 = 4 nên k = 2 hoặc k = −2.
• Trường hợp 1: k = 2 thì x = 2 . 2 = 4; y = 7 . 2 = 14.
• Trường hợp 2: k = −2 thì x = 2 . (−2) = −4; y = 7 . (−2) = −14.
Lời giải:
Gọi chiều rộng và chiều dàu của hình chữ nhật đã cho lần l5ượt là x (m) và y(m).
Do tỉ số giữa chiều rộng và chiều dài là nên hay .
Đặt (k > 0).
Khi đó, ta có x = 2k; y = 5k.
Do diện tích của hình chữ nhật là 40 m2 nên xy = 40.
Suy ra 2k . 5k = 40 hay 10k2 = 40, tức là k2 = 4.
Ta thấy 22 = (−2)2 = 4 mà k > 0 nên k = 2.
Do đó x = 2 . 2 = 4 (m) và y = 5 . 2 = 10 (m).
Chu vi của hình chữ nhật đó là:
2 . (4 + 10) = 28 (m).
Vậy chu vi của hình chữ nhật đó là 28 m.
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 8 : Đại lượng tỉ lệ nghịch
Lý thuyết Tỉ lệ thức
1. Định nghĩa
Tỉ lệ thức là đẳng thức của hai tỉ số và , viết là .
Chú ý: Tỉ lệ thức còn được viết là a : b = c : d; các số a, b, c, d gọi là các số hạng của tỉ lệ thức.
Ví dụ: Tỉ lệ thức hay còn được viết là 3 : 4 = 6 : 8.
2. Tính chất
2.1 Tính chất 1
Nếu thì ad = bc.
Ví dụ: Từ tỉ lệ thức suy ra 3.8 = 4.6 = 24.
2.2 Tính chất 2
Nếu ad = bc và a, b, c, d đều khác 0 thì ta có các tỉ lệ thức:
; ; ; .
Ví dụ: Từ đẳng thức 2 . 6 = 3 . 4 có thể suy ra bốn tỉ lệ thức sau:
; ; ; .
Nhận xét: Với a, b, c, d đều khác 0 thì từ một trong năm đẳng thức sau đây, ta có thể suy ra các đẳng thức còn lại.
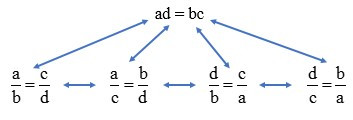
Ví dụ: Từ đẳng thức ta cũng có thể suy ra bốn đẳng thức nữa đó là:
14 . 3 = 6 . 7; ; ; .