Cách tính Đường cao trong tam giác 2024 đầy đủ, chi tiết

Quý Lê Xuân Ngày: 10-09-2024 Lớp 7

Tải xuống 2 2 K 7

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Cách giải đường cao trong tam giác Toán lớp 7, tài liệu bao gồm 2 trang, tuyển chọn bài tập Cách giải đường cao trong tam giác có phương pháp giải chi tiết và bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Cách giải đường cao trong tam giác (ảnh 1)

ĐƯỜNG CAO TRONG TAM GIÁC

A. Lý thuyết

1. Trong một tam giác, đoạn vuông góc vẽ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.

2. Ba đường cao của một tam giác cùng đi qua một điểm (h.20.2). Điểm này gọi là trực tâm của tam giác.

3. Bổ sung tính chất của tam giác cân

- Trong một tam giác cân, đường trung trực ứng với cạnh đáy, đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.

- Trong một tam giác, nếu hai trong bốn loại đường trùng nhau thì tam giác đó là một tam giác cân.

B. Công thức tính đường cao trong tam giác

1. Tính đường cao trong tam giác thường

Tính đường cao trong tam giác thường

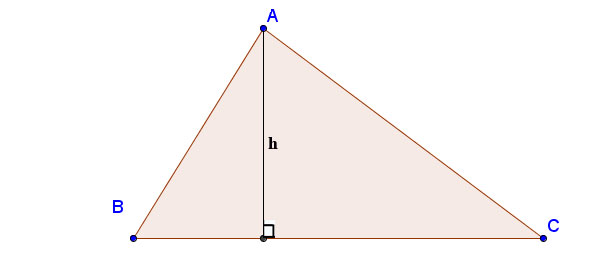
Cách tính đường cao trong tam giác sử dụng công thức Heron:

$h_a=2 \frac{\sqrt{p(p-a)(p-b)(p-c)}}{a}$

Với a, b, c là độ dài các cạnh; ha là đường cao được kẻ từ đỉnh A xuống cạnh BC; p là nửa chu vi:

$p=\frac{(a+b+c)}{2}$

Ví dụ:

Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH kể từ A cắt BC tại H và tính diện tích ABC.

Giải:

Nửa chu vi tam giác: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Chiều cao $AH=2 \frac{\sqrt{p(p-A B)(p-A C)(p-B C)}}{A B}$ $=2 \frac{\sqrt{8(8-4)(8-5)(8-7)}}{4}$

=> $AH = 4 \sqrt{8}(cm)$

Xét tam giác ABC, ta có:

$S_{A B C}=\frac{1}{2} \mathrm{AH} \cdot \mathrm{BC}=\frac{1}{2} 4 \sqrt{8} \times 7=14 \sqrt{8}\left(cm^2\right)$

Như vậy, $\mathrm{AH}=4 \sqrt{8}(cm), S_{A B C}=14 \sqrt{8}\left(cm^2\right)$

2. Công thức tính đường cao trong tam giác cân

Tam giác cân

Giả sử các bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như hình trên:

Công thức tính đường cao AH:

Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến nên:

⇒ HB=HC= ½BC

Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Ví dụ: Cho Δ ABC cân tại A có BC = 30(cm), đường cao AH = 20(cm). Tính đường cao ứng với cạnh bên của tam giác cân đó.

Giải: Xét Δ ABC cân tại A có BC = 30(cm)

⇒ BH = CH = 15(cm).

Áp dụng đinh lý Py – ta – go ta có:

$AB=\sqrt{\left(AH^2+HB^2\right)}$ $=\sqrt{\left(20^2+15^2\right)} =25 cm$

Kẻ $\mathrm{BK} \perp \mathrm{AC}$ , giờ ta phải tính BK = ?

Ta có: $\mathrm{S}_{\mathrm{ABC}}=\frac{1}{2} \cdot\mathrm{AH} \cdot \mathrm{BC}$ $=\frac{1}{2}.20.30\ =\ 300 (cm^{2})$

Mặt khác $\mathrm{S}_{\mathrm{ABC}}=\frac{1}{2} \cdot \mathrm{BK} \cdot \mathrm{AC}=\frac{1}{2} \cdot \mathrm{BK} \cdot 25$

Do đó, ta có $\frac{1}{2}.BK.25 = 300$ ⇔ $BK=\frac{2.300}{25}=24(cm)$

3. Công thức tính đường cao trong tam giác vuông

Tam giác vuông

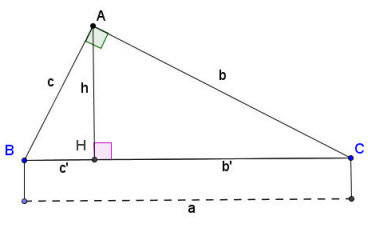
Giả sử có tam giác vuông ABC vuông tại A như hình vẽ trên:

Công thức tính cạnh và đường cao trong tam giác vuông:

1. a²= b²+ c²

2. b²= a.b′ và c²= a.c′

3. a.h = b.c

4. h²= b′.c'

5. $\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}$

Trong đó:

a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;
b’ là đường chiếu của cạnh b trên cạnh huyền;
c’ là đường chiếu của cạnh c trên cạnh huyền;
h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.

Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.

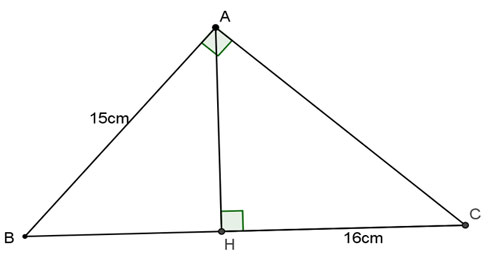
Cho tam giác ABC vuông tại A, đường cao AH

Giải:

Áp dụng hệ thức lượng trong tam giác vuông ABC có:

AC² = CH.BC = 16.BC

Theo định lí Pythagore cho tam giác ABC vuông gại A ta có:

AB² + AC² = BC²

⇔ 15² + 16.BC = BC²

⇔ BC² - 16.BC - 225 = 0

⇔ BC² - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 hoặc BC = -9 (loại)

⇒ AC² = 16.BC = 16.25 = 400 ⇒ AC = 20 (cm)

Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)

=> AH = AB.AC/BC = 15.20/25 = 12(cm)

Vậy BC=25(cm); AC=20(cm); AH=12(cm)

Ví dụ 2:

Cho tam giác ABC vuông tại A, AB=24cm, AC=32cm. Đường trung trực của BC cắt AC, BC theo thứ tự D và E. Tính DE.

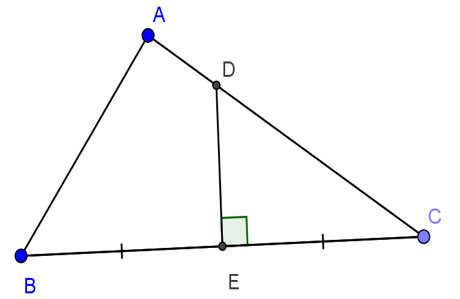
Cho tam giác ABC vuông tại A

Giải:

Xét tam giác vuông ABC, ta có:

BC² = AB²+ AC² ( theo định lý py-ta-go)

BC² = 24²+ 32²

BC² = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Xét tam giác vuông ACB và tam giác vuông ECD có:

Có ∠A = ∠E = 90o

∠C chung

=> Tam giác ACB ∾ tam giác ECD (g.g)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Vậy ED = 15cm

4. Tính đường cao trong tam giác đều

Tính đường cao trong tam giác đều

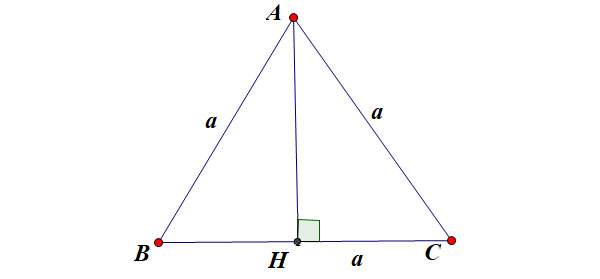
Giả sử tam giác đều ABC có độ dài cạnh bằng a như hình vẽ:

$h=a \frac{\sqrt{3}}{2}$

Trong đó:

h là đường cao của tam giác đều
a là độ dài cạnh của tam giác đều

C. Bài tập tự luyện

Câu 1. Cho $Δ A B C$ ở miền ngoài tam giác vẽ các tam giác đều ABE và ACF. Gọi H là trực tâm của $Δ A B E$ . I là trung điểm của BC. Tính các góc của $Δ F I H .$

Câu 2. Cho góc nhọn xOy, trên 2 cạnh Ox, Oy lần lượt lấy 2 điểm A và B sao cho OA = OB, tia phân giác của góc xOy cắt AB tại I.

a) Chứng minh $O I ⊥ A B .$

b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OI. Chứng minh $B C ⊥ O x .$

Câu 3. Cho góc nhọn xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H dựng các đường vuông góc HA, HB xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).

a) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH. Chứng minh $B C ⊥ O x .$

b) Khi góc xOy bằng $60^{o}$ , chứng minh OA = 2OD.

Câu 4. Cho tam giác ABC cân tại A, trung tuyến AM, đường cao BE. Trên tia BE lấy điểm F sao cho $B F = C E$ . Chứng minh rằng ba đường thẳng BE, CF và AM cùng đi qua một điểm.

Câu 5. Cho tam giác nhọn ABC,hai đường cao BD,CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. Chứng minh rằng $\hat{K A B} = \hat{K C B}$ .

Câu 6. Tam giác ABC có cạnh BC là cạnh lớn nhất. Trên cạnh BC lấy điểm D và E sao cho $B D = B A$ và $C E = C A$ . Tia phân giác của góc B cắt AE tại M. Tia phân giác của góc C cắt AD tại N. Chứng minh rằng tia phân giác của góc $B A C$ vuông góc với MN.

Câu 7. Cho tam giác ABC vuông tại A, vẽ đường cao AH. Gọi M,N lần lượt là trung điểm của AH và HC. Chứng minh rằng $B M ⊥ A N$ .

Câu 8. Cho tam giác ABC đường cao AH. Trên nửa mặt phẳng chứa điểm A bờ là đường thẳng BC lấy điểm D,E sao cho $B D ⊥ B A$ , $B D = B A$ , $C E ⊥ C A$ , $C E = C A$ . Chứng minh rằng các đường thẳng AH, BE, CD đồng quy.

Câu 9. Cho tam giác ABC đường cao AH. Vẽ HD ⊥ AB. Tia phân giác của góc AHC cắt AC tại F. Biết AB = 6cm, AC = 8cm, BC = 10 cm. Tính:

a) Độ dài AH

b) Chu vi tam giác ADF

Câu 10. Cho tam giác ABC vuông tại A, AB : AC = 7 : 24, BC = 625 cm. Tính độ dài hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Câu 11. Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9cm. Tính độ dài BC và AH

Câu 12. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB/AC = 20/21 và AH = 420. Tính chu vi tam giác ABC

Câu 13. Cho tam giác ABC vuông tại A, đường cao AH

Cho biết AC/AB = √2; HC - HB = 2cm.Tính:

a) Tỉ số HC : HB

b) Các cạnh của tam giác ABC

Câu 14. Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Trên HB, HC lần lượt lấy các điểm M, N sao cho góc AMC bằng góc ANB bằng 90⁰. Chứng minh rằng AM = AN

Tài liệu có 2 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm