Tailieumoi.vn xin giới thiệu đến các quý thầy cô Giáo án Toán học 7 bài 3: Quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giác hay nhất theo mẫu Giáo án môn Toán học chuẩn của Bộ Giáo dục. Hi vọng tài liệu này sẽ giúp thầy/cô dễ dàng biên soạn chi tiết Giáo án môn Toán học lớp 7. Chúng tôi rất mong sẽ được thầy/cô đón nhận và đóng góp những ý kiến quý báu của mình.
Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:
|
§3. QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC. BẤT ĐẲNG THỨC TAM GIÁC
|
I. MỤC TIÊU:
HS hiểu cách chứng minh định lí bất đẳng thức tam giác dựa trên quan hệ cạnh và góc trong một tam giác.
- Năng lực chung: Tư duy, gqvđ, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
|
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
|
1. Bất đẳng thức tam giác |
Biết được bất đẳng thức tam giác |
Hiểu cách chứng minh bất đẳng thức tam giác. |
|
|
|
2. Hệ quả của bất đẳng thức tam giác |
|
|
Vận dụng hệ quả của bất đẳng thức tam giác. |
|
III. HOẠT ĐỘNG DẠY - HỌC:
* Kiểm tra bài cũ: (7’)
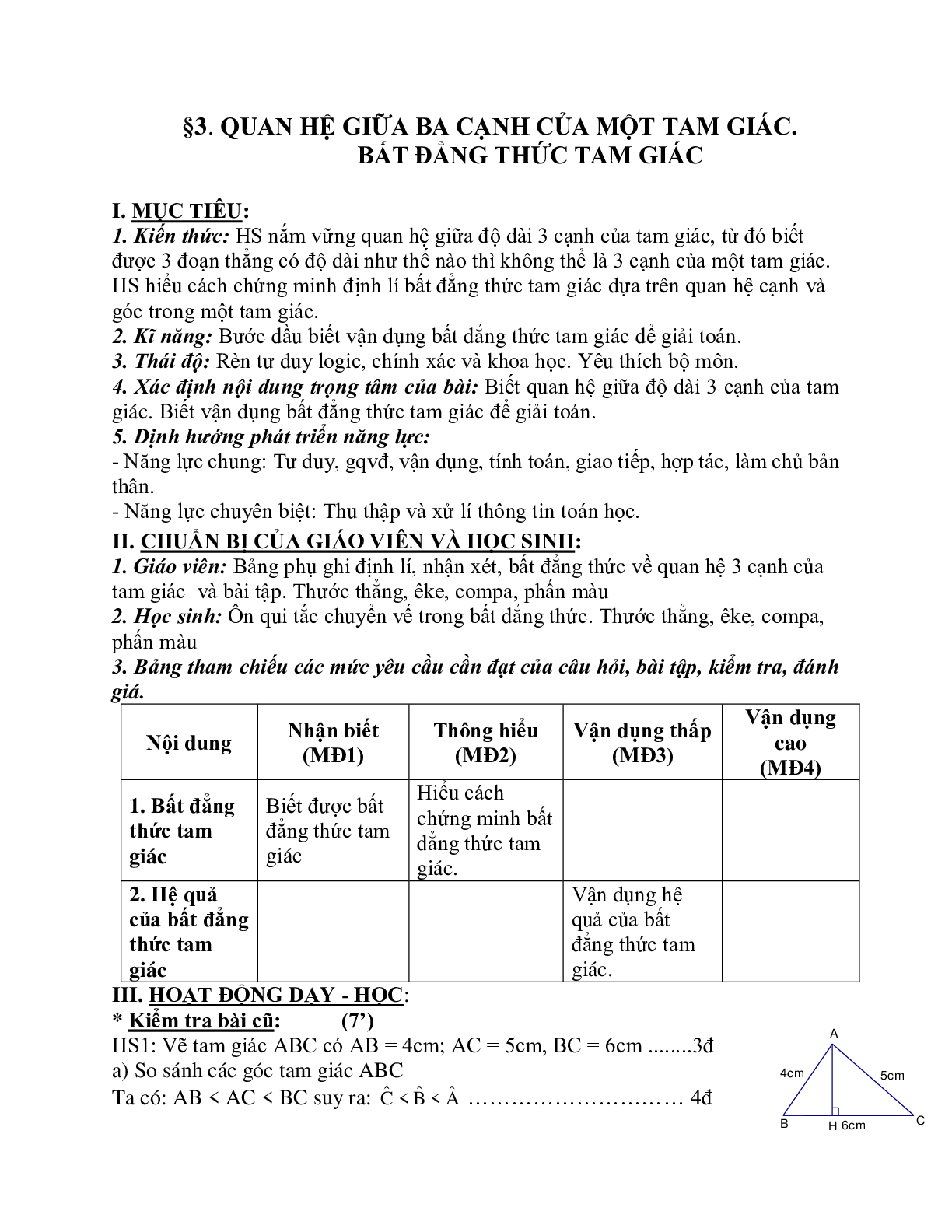
HS1: Vẽ tam giác ABC có AB = 4cm; AC = 5cm, BC = 6cm ........3đ
Ta có: AB < AC < BC suy ra: ………………………… 4đ
Ta có: AB > BH ; AC > HC ………………………….............. 3đ
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Câu trả lời của Hs
|
Hoạt động của GV |
Hoạt động của HS |
|
GV: Từ kết quả phần KTBC em có nhận xét gì về tổng độ dài 2 cạnh bất kì của tam giác ABC so với độ dài cạnh còn lại? GV: Ta hãy xét xem nhận xét này có đúng với mọi tam giác hay không? Đó là nội dung bài học hôm nay chúng ta sẽ tìm hiểu về mối quan hệ giữa độ dài 3 cạnh của một tam giác. Bất đẳng thức tam giác. |
HS: Trong độ dài 2 cạnh bất kì của tam giác lớn hơn độ dài cạnh còn lại của tam giác ABC (4 + 5 > 6; 4 + 6 > 5; 6 + 5 > 4) HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
|
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
||||||
|
HOẠT ĐỘNG 2. Bất đẳng thức tam giác. (18’) (1) Mục tiêu: HS nhận biết được quan hệ giữa độ dài ba cạnh của một tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập. (5) Sản phẩm: Lời giải bài toán ?1, ?2 và nội dung định lý. |
|||||||||
|
1. Bất đẳng thức tam giác Định lí (Sgk/61)
Chứng minh - Trên tia đối của tia AB lấy điểm D sao cho AD = AC. Nối CD Có BD = BA +AC - Có A nằm giữa B và D nên tia CA nằm giữa 2 tia CB và CD nên > - Mà ACD cân do AD = AC = () >
|
GV: Yêu cầu HS thực hiện GV: Hãy thử vẽ tam giác với các cạnh có độ dài: a) 1cm, 2cm, 4cm b) 1cm, 3cm, 4cm H: Em có nhận xét gì? H: có 1 +2 < 4; 1+ 3 = 4 Vậy trong mỗi trường hợp, tổng độ dài 2 cạnh nhỏ so với đoạn lớn nhất như thế nào? GV: Như vậy, không phải 3 độ dài nào cũng là độ dài 3 cạnh của 1 tam giác. Ta có định lí sau. H: Hãy cho biết GT và KL của định lí? GV: Ta sẽ chứng minh bất đẳng thức đầu tiên H: Làm thế nào để tạo ra 1 tam giác có 1 cạnh là BC, một cạnh bằng AB + AC để so sánh chúng? GV hướng dẫn HS phân tích.
H: Làm thế nào để chứng minh BD > BC
H: Tại sao >
H: bằng góc nào?
GV: Các bất đẳng thức còn lại chứng minh tương tự, ta có: AB + BC > AC AC + BC > AB đó là nội dung bài tập 29.Sgk/64 GV: Giới thiệu các bất đẳng thức ở phần KL của định lí được gọi là bất đẳng thức tam giác. |
HS thực hiện HS cả lớp làm vào vở 1HS lên bảng thực hiện
HS: Không vẽ được tam giác có độ dài các cạnh như vậy HS: Vậy tổng độ dài 2 đoạn nhỏ, nhỏ hơn hoặc bằng độ dài đoạn lớn nhất
HS: Đọc định lí
HS vẽ hình và ghi GT, KL của định lí
-Trên tia đối của tia AB lấy điểm D sao cho AD = AC. Nối CD, Có BD = BA + AC HS nghe GV hướng dẫn HS phân tích: HS: Muốn chứng minh BD > BC ta cần có > HS: Có A nằm giữa B và D nên tia CA nằm giữa 2 tia CB và CD nên > - Mà ACD cân do AD = AC =(=) > HS trình bày miệng bài toán
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
||||||
|
HOẠT ĐỘNG 3. Hệ quả của bất đẳng thức tam giác. (9’) (1) Mục tiêu: HS nhận biết được 3 đoạn thẳng có độ dài như thế nào thì không thể là ba cạnh của một tam giác. (2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi. (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập. (5) Sản phẩm: Vận dụng hệ quả của bất đẳng thức tam giác. |
|||||||||
|
2. Hệ quả của bất đẳng thức tam giác
Từ các bất đẳng thức suy ra: AB > AC – BC; AB > BC – AC; AC > AB – BC; AC > BC – AB; BC > AC – AB; BC > AB – AC;
* Hệ quả: SGK/62.
* Nhận xét: SGK/62.
AB – BC < AC < AB + BC AC – BC < AB < AC + BC AB – AC < BC < AB + AC
Lưu ý: SGK/63. |
GV: Hãy nêu lại các bất đẳng thức tam giác.
GV: Phát biểu qui tắc chuyển vế của BĐT GV: Yêu cầu học sinh viết 3 bất đẳng thức tam giác. Dùng quy tắc chuyển vế ta được hệ quả. Hãy phát biểu hệ quả này bằng lời Kết hợp với các bất đẳng thức tam giác, ta có: AC – AB < BC < AB + AC Hãy phát biểu nhận xét trên bằng lời Hãy điền và dấu …. trong các bất đẳng thức … < AB < … … < AC < … Yêu cầu HS làm
Cho HS đọc phần lưu ý |
HS: Trong ABC: AB + AC > BC; AB + BC > AC; AC + BC > AB HS phát biểu qui tắc
HS: BC-AC < AB < BC+AC BC-AB < AC < BC+AB
Phát biểu hệ quả này bằng lời
HS phát biểu nhận xét trên bằng lời
HS trả lời miệng.
HS: không có tam giác với 3 cạnh dài 1cm, 2cm, 4cm vì 1+ 2 < 4 HS đọc phần lưu ý
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân. |
||||||
C. LUYỆN TẬP, CỦNG CỐ (8’)
(1) Mục tiêu: Củng cố kiến thức về bất đẳng thức tam giác. Hs vận dụng để giải được các bài tập ở các mức độ NB, TH, VD.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi
(3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Lời giải các bài tập 1, 2, 3.
|
+ Chuyển giao: GV: Yêu cầu HS làm bài tập Bài 1: Cho tam giác MNP khi đó MN + NP > PM và MP – MN < NP. Hãy điền dấu >, < thích hợp vào chỗ trống MP + NP … MN; MN – MP … PN Bài 2: 1) Có hay không một ∆ mà độ dài 3 cạnh của nó tương ứng là 2cm; 3cm; 6cm? Vì sao? 2) Bộ ba đoạn thẳng nào không thể là ba cạnh của một tam giác: a) 2cm ; 3cm ; 6cm b) 2cm ; 4cm ; 6cm c) 3cm ; 4cm ; 6cm 3) Bạn Lan nói: Muốn biết độ dài ba đoạn thẳng nào đó có tương ứng là độ dài ba cạnh của một ∆ hay không ta chỉ cần so sánh độ dài lớn nhất với tổng hai độ dài còn lại hoặc so sánh độ dài nhỏ nhất với hiệu hai độ còn lại. Theo em bạn Lan nói đúng hay không vì sao? Bài 3: Cho tam giác ABC có AH ^ BC tại H. So sánh AB và BH; AC và CH Từ đó hãy nêu một cách khác để chứng minh bất đẳng thức tam giác.
|
HS: Thảo luận nhóm làm bài
1) Không vì 2 + 3 < 6
2) 2cm ; 3cm ; 6cm 2cm ; 4cm ; 6cm
3) Bạn Lan nói đúng vì bạn đã vận dụng theo Bất đẳng thức tam giác về hệ quả của nó
AB > BH AC > CH Þ AB + AC > BH + CH = BC |
Năng lực tư duy, vận dụng, giao tiếp, làm chủ bản thân, hợp tác. |
D. HƯỚNG DẪN VỀ NHÀ (2’)
- Nắm vững bất đẳng thức tam giác, học cách chứng minh định lí bất đẳng thức tam giác
- BTVN: 16, 17, 18, 19 Sgk/63
- Tiết sau luyện tập.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
Bài 1 (MĐ1); Bài 2 (MĐ2); Bài 3 (MĐ3)
LUYỆN TẬP
I. MỤC TIÊU:
- Năng lực chung: Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, hợp tác, làm chủ bản thân.
- Năng lực chuyên biệt: Thu thập và xử lí thông tin toán học.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
|
Nội dung |
Nhận biết (MĐ1) |
Thông hiểu (MĐ2) |
Vận dụng thấp (MĐ3) |
Vận dụng cao (MĐ4) |
|
1. Quan hệ giữa ba cạnh của tam giác. |
Biết quan hệ giữa độ dài ba cạnh của tam giác. |
Hiểu cách chứng minh bất đẳng thức tam giác. |
Biết vận dụng quan hệ giữa độ dài ba cạnh của tam giác để giải bài toán.
|
Sử dụng định lý trong các bài toán thực tê. |
III. HOẠT ĐỘNG DẠY - HỌC:
* Kiểm tra bài cũ: (7')
HS1: Phát biểu nhận xét quan hệ ba cạnh của một tam giác. Minh hoạ bằng hình vẽ và ghi bất đẳng thức.
Trả lời: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.........……….4đ
BC –AC < AB < BC + AC.........……….2đ
BC – AB < AC < BC + AB……….2đ
AC – AB < BC < AB + AC……….2đ
HS2: Làm bài tập 16 Sgk/63.
Đáp án: Có AC – BC < AB < AC + BC.........................3đ
Hay 7 – 1 < AB < 7 + 1
6 < AB < 8 .........................2đ
Mà độ dài AB là một số nguyên AB = 7cm .........................2đ
Do đó tam giác ABC cân tại A. .........................3đ
Gv nhận xét và cho điểm.
A. KHỞI ĐỘNG
HOẠT ĐỘNG 1. Tình huống xuất phát (mở đầu) (1’)
(1) Mục tiêu: Kích thích hs suy đoán, hướng vào bài mới
(2) Phương pháp/Kĩ thuật dạy học: Phương pháp vấn đáp – gợi mở/Kỹ thuật động não
(3) Hình thức tổ chức hoạt động: Toàn lớp
(4) Phương tiện dạy học: Bảng, phấn.
(5) Sản phẩm: Không
|
Hoạt động của GV |
Hoạt động của HS |
|
GV: Ở tiết học trước các em đã được biết quan hệ giữa ba cạnh của một tam giác. Tiết học hôm nay các em sẽ được củng cố kiến thức về quan hệ giữa ba cạnh của một tam giác thông qua giải một số bài tập. |
HS lắng nghe
|
B. HÌNH THÀNH KIẾN THỨC
|
Nội dung |
Hoạt động của GV |
Hoạt động của HS |
NL hình thành |
|
HOẠT ĐỘNG 2. Luyện tập (27’) (1) Mục tiêu: HS vận dụng quan hệ giữa ba cạnh của một tam giác để giải bài toán liên quan đến tính thực tế. (2) Phương pháp/Kĩ thuật dạy học: Vấn đáp gợi mở, luyện tập thực hành, trực quan/ kỹ thuật đặt câu hỏi, kỹ thuật động não, kỹ thuật thu nhận thông tin phản hồi (3) Hình thức tổ chức hoạt động: HĐ cá nhân, nhóm, cả lớp (4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập. (5) Sản phẩm: Lời giải các bài toán. |
|||
|
1. Bài 18. Sgk/63 a) 2cm; 3cm; 4cm Vì 4cm < 2cm + 3cm => Vẽ được tam giác với độ dài ba đoạn thẳng trên. b) 1cm; 2cm; 3,5cm Ta có: 3,5cm > 1cm + 2cm => Không vẽ được tam giác với độ dài ba đoạn thẳng là 1cm; 2cm; 3,5cm c) 2,2cm; 2cm; 4,2cm Vì 4,2cm = 2cm + 2,2cm Nên không vẽ được tam giác với độ dài ba đoạn thẳng là 2,2cm; 2cm; 4,2cm
2. Bài 19. Sgk/63: Gọi độ dài cạnh thứ ba của tam giác cân là x (cm). Theo bất đẳng thức tam giác ta có: 7,9 – 3,9 < x < 7,9 + 3,9. 4 < x < 11,8 x = 7,9 (cm) Chu vi của tam giác cân là:
3. Bài 21. Sgk/64: Tam giác ABC, có: AC + CB > AB (bđt tam giác) Nên AC + CB ngắn nhất khi AC + CB = AB Hay điểm C nằm giữa hai điểm A và B Khi đó 3 điểm A, B, C thẳng hàng Phải dựng cột điện tại điểm C thuộc đường thẳng AB (bên bờ sông gần khu dân cư) để độ dài đường dây dẫn là ngắn nhất. |
GV: Nêu bài 18 Sgk (đưa đề bài lên bảng phụ) H: Muốn biết độ dài ba đoạn thẳng có phải là ba cạnh của một tam giác hay không ta làm như thế nào? GV: Yêu cầu Hs làm bài trên vở nháp Sau 2’ giáo viên thu một vài bài chấm điểm và gọi Hs lên bảng trình bày. GV: Yêu cầu Hs dưới lớp nhận xét. Giáo viên uốn nắn sửa theo đáp án GV: nêu bài 19 tr63 Sgk H: chu vi của tam giác là gì? H: Vậy trong hai cạnh dài 3,9 cm và 7,9 cm , cạnh nào sẽ là cạnh thứ ba, cạnh nào sẽ là cạnh bên của tam giác cân? Làm thế nào để biết ? GV: yêu cầu HS tính chu vi tam giác cân. GV: nêu bài 21 (đưa đề bài và hình vẽ lên bảng phụ), giới thiệu trạm biến áp A, khu dân cư B, cột điện C. H: Cột điện C ở vị trí nào để độ dài AB ngắn nhất?
|
HS: Đọc đề bài 18 Sgk. HS: Đứng tại chỗ trả lời
HS: Thảo luận làm bài theo nhóm
Hs lên bảng trình bày.
HS: Nhận xét
HS: Trả lời là tổng ba cạnh của tam giác đó. HS: dựa vào bất đẳng thức tam giác
HS: trình bày cách xác định cạnh của tam giác cân. HS: tính chu vi tam giác HS: quan sát đề bài trên bảng thảo luận và trình bày
HS: Vị trí cột điện C là giao của bờ sông với đường thẳng AB
|
Năng lực tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, làm chủ bản thân.
|
C. LUYỆN TẬP: Đã thực hiện ở mục B
D. VẬN DỤNG, TÌM TÒI, MỞ RỘNG
HOẠT ĐỘNG 3. Tìm tòi, mở rộng (8’)
(1) Mục tiêu: Giúp HS tăng cường ý thức tự tìm hiểu, mở rộng kiến thức và sự hiểu biết của mình thông qua các câu hỏi thực tiễn.
(2) Phương pháp/Kĩ thuật dạy học: Vấn đáp, thực hành, trực quan/ kỹ thuật động não.
(3) Hình thức tổ chức hoạt động: Hoạt động nhóm, cả lớp
(4) Phương tiện dạy học: Bảng, phấn, sgk, bảng phụ, dụng cụ học tập.
(5) Sản phẩm: Các tư liệu mà học sinh sưu tầm được liên quan đến các yếu tố trong tam giác
|
*Bài tập 22. Sgk/64: DABC, có: 90 – 30 < BC < 90 + 30 Hay 60 < BC < 120 a) Nếu đặt máy phát ở C với bán kính hoạt động là 60 km thì thành phố B không nhận được tín hiệu. b) Nếu đặt máy phát ở C với bán kính hoạt động là 120 km thì thành phố B nhận được tín hiệu. |
+ Chuyển giao: Bài tập (treo bảng phụ) H: Bài tập 22 cho ta biết và yêu cầu chứng minh điều gì? H: Muốn biết ba tỉnh có nhận được tín hiệu hay không thì ta cần chỉ ra khoảng cách giữa ba thành phố phải nhỏ hơn bán kính phát sóng. Vậy có kết luận gì?
|
HS: Hoạt động nhóm, đại diện trả lời. |
Năng lực sáng tạo, làm chủ bản thân.
|
E. HƯỚNG DẪN VỀ NHÀ (2’)
- Học thuộc quan hệ giữa ba cạnh của một tam giác thể hiện bằng bất đẳng thức tam giác.
- Xem các bài tập đã giải. BTVN 25, 27, 29, 30/26 – 27 SBT.
- Tiết sau học “Tính chất ba đường trung tuyến của tam giác”, mỗi HS chuẩn bị một tam giác bằng giấy và một mảnh giấy kẻ ô vuông mỗi chiều 10 ô như hình 22 tr 65 Sgk. Mang compa, thước thẳng có chia khoảng.
- Ôn khái niệm trung điểm của đoạn thẳng và cách xác định trung điểm đoạn thẳng bằng thước và cách gấp giấy.
* NỘI DUNG CÁC CÂU HỎI, BÀI TẬP
GV: Củng cố bài lồng ghép vào quá trình luyện tập.
Các bài tập củng cố thể hiện trong "Hoạt động 2, 3". (MĐ2, 3, 4)