§8. TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC

Nội dung

Nhận biết

(MĐ1)

Thông hiểu

(MĐ2)

Vận dụng thấp

(MĐ3)

Vận dụng cao

(MĐ4)

1. Đường trng trực của tam giác 

Nhận biết được đường trung trực của tam giác. Biết vẽ 3 đường trung trực của tam giác

2. Tính chất ba đường trung trực  của tam giác

Biết ba đường trung trực của tam giác đồng quy tại một điểm, điểm đó cách đều ba đỉnh của tam giác.

Hiểu chứng minh sự đồng quy của ba đường trung trực

Vận dụng tính chất ba đường trung trực của tam giác

Hoạt động của GV

Hoạt động của HS

GV: Ở tiết học trước ta được ôn lại đường trung trực của một đoạn thẳng và tính chất của nó. Vậy đường trung trực của tam giác được xác định như thế nào và có tính chất gì đặc biệt? Chúng ta sẽ nghiên cứu qua bài học hôm nay.

HS lắng nghe

Nội dung

Hoạt động của GV

Hoạt động của  HS

NL hình

thành

HOẠT ĐỘNG 2: Đường trung trực của tam giác. (10’)

(1) Mục tiêu: HS biết khái niệm đường trung trực của tam giác.

(2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi.

(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp.

(4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập

(5) Sản phẩm: HS vễ được đường trung trực của tam giác.

1. Đường trung trực của tam giác.

a là đường trung trực của tam giác ABC. Mỗi tam giác có ba đường trung trực.

*Trong một tam giác cân đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.

GV đưa hình lên bảng phụ và hỏi: Vậy một tam giác có mấy đường trung trực?

H: Trong một tam giác bất kỳ đường trung trực của một cạnh có nhất thiết đi qua đỉnh đối diện với cạnh ấy hay không ?

Trường hợp nào đường trung trực của một tam giác  đi qua đỉnh đối diện với cạnh ấy

H: Đoạn thẳng DI nối đỉnh của tam giác với trung điểm của cạnh đối diện. Vậy DI là đường gì của D DEF? (Phần KTBC)

GV từ c/minh trên ta có tính chất

GV nhấn mạnh: trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là trung trực của cạnh đáy, cũng đồng thời là đường trung tuyến của tam giác.

HS: có 3 đường trung trực

HS: Trả lời

HS: Đoạn thẳng DI là đường trung tuyến của D DEF

Tư duy, giải quyết vấn đề, vận dụng, giao tiếp làm chủ bản thân.

HOẠT ĐỘNG 3: Tính chất ba đường trung trực của tam giác. (16’)

(1) Mục tiêu: HS biết tính chất ba đường trung trực của tam giác. Biết xác định giao ba đường trung trực của một tam giác.

(2) Phương pháp/Kĩ thuật dạy học: Tái hiện kiến thức, thu thập thông tin, thuyết trình, vấn đáp/ kỹ thuật đặt câu hỏi, động não, thu nhận thông tin phản hồi.

(3) Hình thức tổ chức hoạt động: HĐ cá nhân, cả lớp.

(4) Phương tiện dạy học: Bảng, phấn, sgk, dụng cụ học tập

(5) Sản phẩm: Rút ra tính chất ba đường trung trực của tam giác, giao của ba đường trung trực của tam giác gọi là điểm cách đều 3 đỉnh của tam giác.

2. Tính chất ba đường trung trực của tam giác:

Định lý: Sgk/78

          DABC, b, c là

GT    trung trực của AC

          AB, b cắt c tại O

KL     O nằm trên đường

          Trung trực của BC

          OA = OB = OC

Chứng minh: Sgk

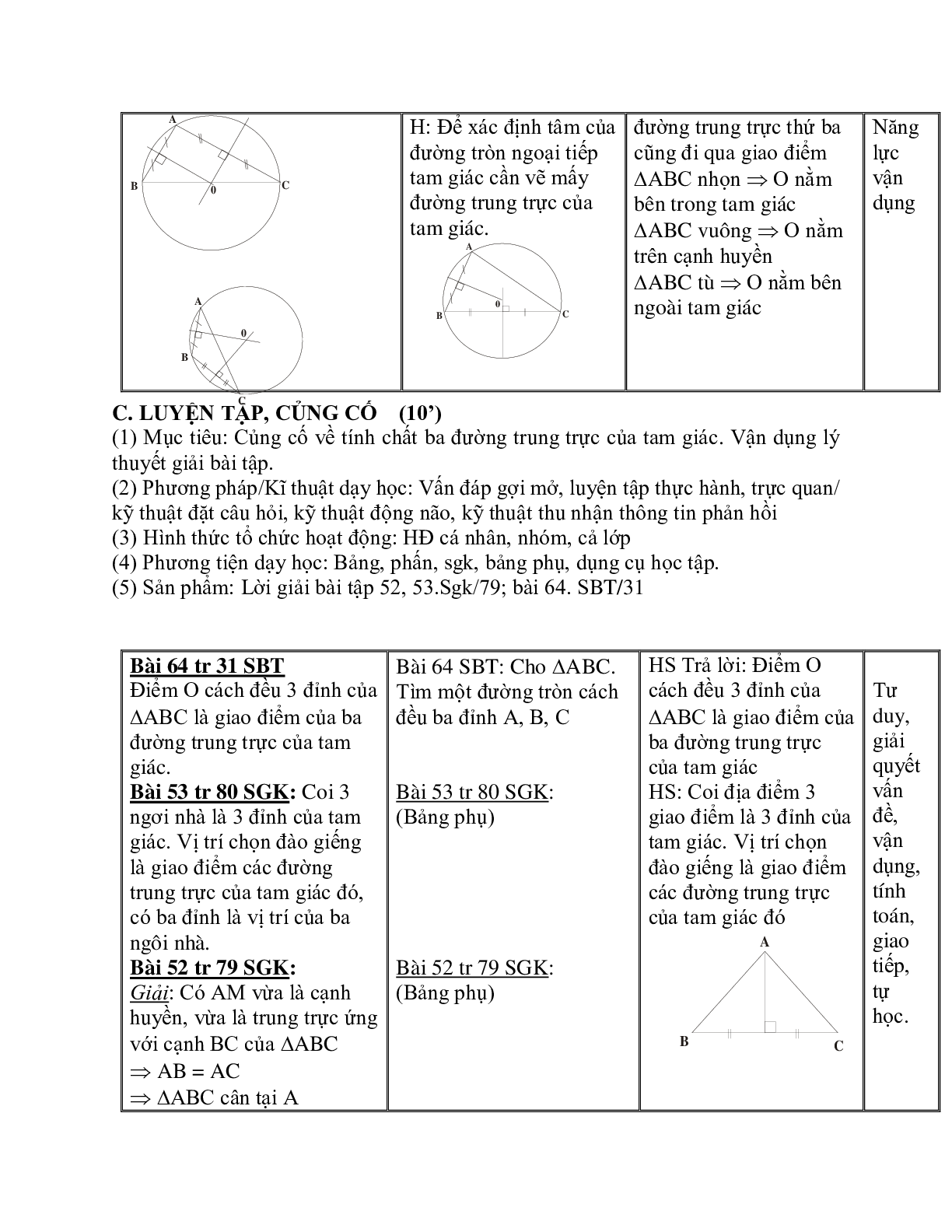
GV yêu cầu HS đọc định lý Sgk/78

H: Hãy nêu GT, KL của định lý?

GV: Để c/m định lý này ta cần dựa trên 2 định lý thuận và định lý đảo của  đoạn thẳng

GV g.thiệu đường tròn ngoại tiếp tam giác  ABC là đường tròn đi qua ba đỉnh của tam giác.

H: Để xác định tâm của đường tròn ngoại tiếp  tam giác cần vẽ mấy đường trung trực của tam giác.

HS: đọc định lý

HS:  nêu GT, KL

Ta chỉ cần vẽ hai đường trung trực của tam giác, giao điểm của chúng sẽ là tâm của đường tròn ngoại tiếp tam giác vì đường trung trực thứ ba cũng đi qua giao điểm

DABC nhọn Þ O nằm bên trong tam giác

DABC vuông Þ O nằm trên cạnh huyền

DABC tù Þ O nằm bên ngoài tam giác

Tư duy, giải quyết vấn đề, giao tiếp làm chủ bản thân

Năng lực vận dụng

Bài 64 tr 31 SBT

Điểm O cách đều 3 đỉnh của DABC là giao điểm của ba đường trung trực của tam giác.

Bài 53 tr 80 SGK: Coi 3 ngơi nhà là 3 đỉnh của tam giác. Vị trí chọn đào giếng là giao điểm các đường trung trực của tam giác đó, có ba đỉnh là vị trí của ba ngôi nhà.

Bài 52 tr 79 SGK:

Giải: Có AM vừa là cạnh huyền, vừa là trung trực ứng với cạnh BC của DABC

Þ AB = AC

Þ DABC cân tại A

Bài 64 SBT: Cho DABC. Tìm một đường tròn cách đều ba đỉnh A, B, C

Bài 53 tr 80 SGK:

(Bảng phụ)

Bài 52 tr 79 SGK:

(Bảng phụ)

HS Trả lời: Điểm O cách đều 3 đỉnh của DABC là giao điểm của ba đường trung trực của tam giác

HS: Coi địa điểm 3 giao điểm là 3 đỉnh của tam giác. Vị trí chọn đào giếng là giao điểm các đường trung trực của tam giác đó

Tư duy, giải quyết vấn đề, vận dụng, tính toán, giao tiếp, tự học.

Nội dung

Nhận biết

(MĐ1)

Thông hiểu

(MĐ2)

Vận dụng thấp

(MĐ3)

Vận dụng cao

(MĐ4)

1. Đường trung trực của tam giác. Tính chất ba đường trung trực của tam giác .

Biết chứng minh sự đồng quy của ba đường trung trực.

Chứng minh được 3 đường trung trực của một tam giác đồng quy tại một điểm. Điểm đó là tâm đường tròn ngoại tiếp tam giác.

 Vận dụng được đ/l về sự đồng quy của 3 đường trung trực trong 1 tam giác để giải một số bài tập đơn giản.

Hoạt động của GV

Hoạt động của HS

GV: Tiết học trước các em đã nắm được định lý về tính chất ba đường trung trực của tam giác, tiết học hôm nay các em sẽ luyện tập để củng cố kiến thức cho bài học thông qua việc giải một số bài tập thực tế.

HS lắng nghe

Nội dung

Hoạt động của GV

Hoạt động của  HS

NL hình

thành

HOẠT ĐỘNG 2: Luyện tập. (32’)

(1) Mục tiêu: Củng cố các địmh lí về tính chất đường trung trực của một đoạn thẳng, tính chất ba đường trung trực của tam giác.

(2) Phương pháp/Kĩ thuật dạy học: Tái hiện k.thức, thu thập thông tin, thuyết trình, vấn đáp.

(3) Hình thức tổ chức hoạt động: Toàn lớp

(4) Phương tiện dạy học: Bảng, phấn, Sgk, compa, êke và thước thẳng.

(5) Sản phẩm: Học sinh hiểu và vận dụng lý thuyết để giải các bài tập

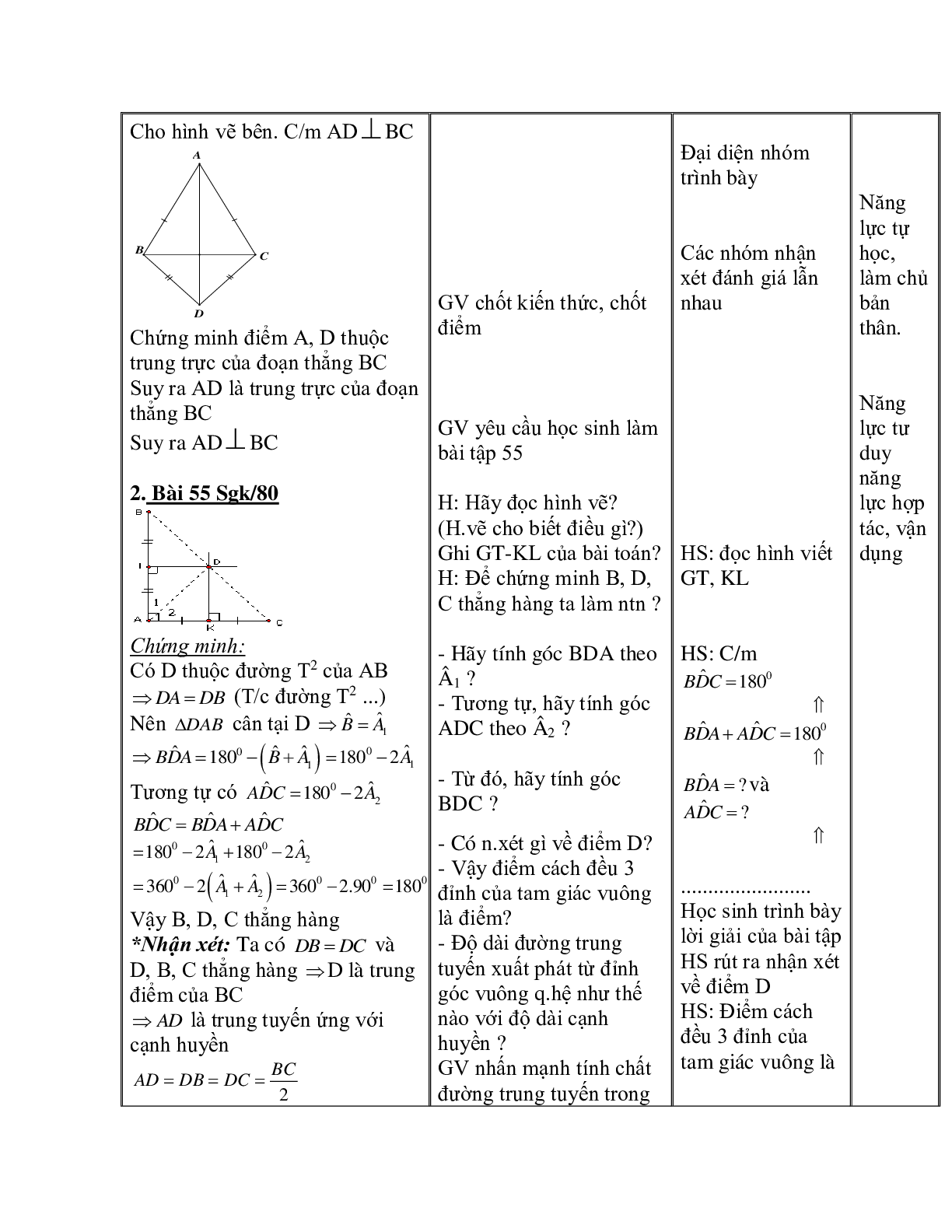
1. Bài tập 1:

Cho hình vẽ bên. C/m ADBC

Chứng minh điểm A, D thuộc trung trực của đoạn thẳng BC

Suy ra AD là trung trực của đoạn thẳng BC

Suy ra ADBC

2. Bài 55 Sgk/80

Chứng minh:

Có D thuộc đường T² của AB

 (T/c đường T² ...)

Nên  cân tại D

Tương tự có

 Vậy B, D, C thẳng hàng

*Nhận xét: Ta có  và D, B, C thẳng hàng D là trung điểm của BC

 là trung tuyến ứng với cạnh huyền

3. Bài 57 Sgk/80

- Lấy 3 điểm A, B, C phân biệt trên cung tròn

- Vẽ đường trung trực của AB, BC. Giao của 2 đường trung trực này là tâm đường tròn bị gãy (điểm O)

- Bán kính của đường viền là khoảng cách từ O đến 1 điểm bất kỳ của cung tròn (= OA)

4. Bài tập

Cho ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D (DBC). Trên tia đối của tia AD lấy E sao cho AE=BD. Chứng minh DCE cân.

GV phát phiếu học tập cho HS

GV chốt kiến thức, chốt điểm

GV yêu cầu học sinh làm bài tập 55

H: Hãy đọc hình vẽ? (H.vẽ cho biết điều gì?)

Ghi GT-KL của bài toán?

H: Để chứng minh B, D, C thẳng hàng ta làm ntn ?

- Hãy tính góc BDA theo Â₁ ?

- Tương tự, hãy tính góc ADC theo Â₂ ?

- Từ đó, hãy tính góc BDC ?

- Có n.xét gì về điểm D?

- Vậy điểm cách đều 3 đỉnh của tam giác vuông là điểm?

- Độ dài đường trung tuyến xuất phát từ đỉnh góc vuông q.hệ như thế nào với độ dài cạnh huyền ?

GV nhấn mạnh tính chất đường trung tuyến trong tam giác vuông và tính chất trung điểm của cạnh huyền.

GV yêu cầu học sinh làm tiếp bài tập 57 (SGK)

(H.vẽ đưa lên bảng phụ)

H: Làm thế nào để xđ được bán kính của đường viền này?

GV yêu cầu học sinh đọc đề bài, vẽ hình, ghi GT, KL

GV hướng dẫn HS phân tích bài toán tìm hướng giải

HS thảo luận nhóm

Đại diện nhóm trình bày

Các nhóm nhận xét đánh giá lẫn nhau

HS: đọc hình viết GT, KL

HS: C/m

Học sinh trình bày lời giải của bài tập

HS rút ra nhận xét về điểm D

HS: Điểm cách đều 3 đỉnh của tam giác vuông là TĐ của cạnh huyền

HS:

Học sinh nghe giảng và ghi bài

Học sinh đọc đề bài và làm bài tập 57

HS: Bước 1: Xác định tâm của đường tròn bị gãy

Bước 2: Xác định khoảng cách từ tâm đến 1 điểm trên đường viền

HS đọc đề bài, vẽ hình, ghi GT, KL

Cá nhân HS phát biểu từng ý

HS về nhà hoàn thiện bài.

Năng lực tự học, làm chủ bản thân.

Năng lực tư duy

năng lực hợp tác, vận dụng