Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các dạng toán về vectơ và các phép toán vectơ, tài liệu bao gồm 34 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu bao gồm các nội dung sau:

A. Hai vécto bằng nhau

B. Tổng và hiệu hai vecto

C. Tích của vecto với một số

Các dạng toán về vectơ và các phép toán vectơ

A. Hai vécto bằng nhau

I. Chứng minh các vécto bằng nhau

Ví dụ 1: Cho tam giác nhọn ABC nội tiếp trong đường tròn tâm O. Gọi H là trực tâm của tam giác ABC. Gọi M, N lần lưọt là trung điểm của BC và AH. Chứng minh: \(\overrightarrow {{\rm{OM}}}  = \overrightarrow {{\rm{AN}}} \)

Giải:

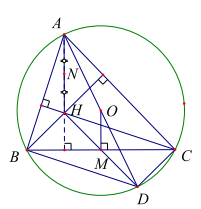
OA kéo dài cắt đường tròn ngọai tiếp tam giác ABC tại D.

Ta có \({\rm{DC}} \bot {\rm{AC}},{\rm{DB}} \bot {\rm{AB}}\) ( góc nội tiếp chắn nửa đường tròn) \( \Rightarrow {\rm{BH}}//{\rm{DC}},{\rm{CH}}//{\rm{DB}} \Rightarrow {\rm{BHCD}}\) là hình bình hành \( \Rightarrow {\rm{H}},{\rm{M}},{\rm{D}}\) thẳng hàng và MH=MD.

Trong tam giác DAH có \({\rm{OM}}//{\rm{AH}}\) và \({\rm{OM}} = \frac{1}{2}{\rm{AH}}\)

Suy ra OM=AN.

Ví dụ 2: Cho hình vuông ABCD. Gọi M,N,P,Q lần lưọt là các điểm trên các cạnh AB, BC, CD và DA sao cho \(\frac{{{\rm{AM}}}}{{{\rm{AB}}}} = \frac{{{\rm{BN}}}}{{{\rm{BC}}}} = \frac{{{\rm{CP}}}}{{{\rm{CD}}}} = \frac{{{\rm{DQ}}}}{{{\rm{DA}}}} = \frac{1}{3}\). Chứng minh rằng: \(\overrightarrow {{\rm{MN}}}  = \overrightarrow {{\rm{QP}}} ,\overrightarrow {{\rm{MQ}}}  = \overrightarrow {{\rm{NP}}} \).

Giải:

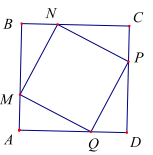
Từ giả thiết ta suy ra \({\rm{AM}} = {\rm{BN}} = {\rm{CP}} = {\rm{DQ}} \Rightarrow {\rm{MNPQ}}\) là hình bình hành \( \Rightarrow \overrightarrow {{\rm{MN}}}  = \overrightarrow {{\rm{QP}}} \) và \(\overrightarrow {{\rm{MQ}}}  = \overrightarrow {{\rm{NP}}} \)

Ví dụ 3: Cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là trung điểm các cạnh AB,BC,CD và DA. Chứng minh rằng: \(\overrightarrow {{\rm{NP}}}  = \overrightarrow {{\rm{MQ}}} ,\overrightarrow {{\rm{PQ}}}  = \overrightarrow {{\rm{NM}}} \).

Giải:

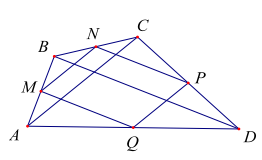
Từ giả thiết ta suy ra MN=PQ và \({\rm{MN}}//{\rm{PQ}}\) vì chúng đều bằng \(\frac{1}{2}{\rm{AC}}\) và đều song song với AC. Vậy tứ giác MNPQ là hình bình hành nên ta có \(\overrightarrow {{\rm{NP}}}  = \overrightarrow {{\rm{MQ}}} ,\overrightarrow {{\rm{PQ}}}  = \overrightarrow {{\rm{NM}}} \)

Ví dụ 4: Cho hình bình hành ABCD. Dựng \(\overrightarrow {{\rm{AM}}}  = \overrightarrow {{\rm{BA}}} ;\overrightarrow {{\rm{MN}}}  = \overrightarrow {{\rm{DA}}} ;\overrightarrow {{\rm{NP}}}  = \overrightarrow {{\rm{DC}}} \). Chứng minh \(\overrightarrow {{\rm{MP}}}  = \overrightarrow {{\rm{DB}}} ;\overrightarrow {{\rm{MD}}}  = \overrightarrow {{\rm{PB}}} \)

Giải:

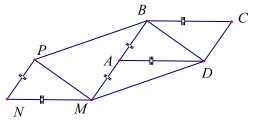
Ta có B, A, M thẳng hàng và AB=AM.

Do \(\overrightarrow {{\rm{MN}}}  = \overrightarrow {{\rm{DA}}}  \Rightarrow {\rm{MN}}//{\rm{DA}}\) và MN=DA.

Do \(\overrightarrow {{\rm{NP}}}  = \overrightarrow {{\rm{DC}}}  = \overrightarrow {{\rm{AB}}}  \Rightarrow {\rm{NP}}//{\rm{AP}}\) và NP=AB

Hai tam giác ABC và NPM bằng nhau và có các cạnh tương ứng song song. Từ đó suy ra MP=DB và \({\rm{MP}}//{\rm{DB}}\). Vậy tứ giác MODB là hình bình hành.

\( \Rightarrow \overrightarrow {{\rm{MP}}}  = \overrightarrow {{\rm{DB}}} ;\overrightarrow {{\rm{MD}}}  = \overrightarrow {{\rm{PB}}} \) (đpcm)

II. Tính độ dài vécto

Ví dụ 5: Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm của AB,N là điểm đối xứng với C qua D. Hãy tính độ dài của các vécto sau: \(\overrightarrow {{\rm{MD}}} ,\overrightarrow {{\rm{MN}}} \).

Giải:

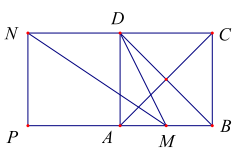
Trong tam giác vuông MAD ta có

\(|\overrightarrow {{\rm{MD}}} | = {\rm{MD}} = \sqrt {{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{M}}^2}}  = \sqrt {{{\rm{a}}^2} + {{\left( {\frac{{\rm{a}}}{2}} \right)}^2}}  = \frac{{{\rm{a}}\sqrt 5 }}{2}\)

Dựng hình vuông ADNP, khi đó \({\rm{PM}} = \frac{{3{\rm{a}}}}{2}\).

Trong tam giác vuông MNP ta có

\(|\overrightarrow {{\rm{MN}}} | = {\rm{MN}} = \sqrt {{\rm{N}}{{\rm{P}}^2} + {\rm{P}}{{\rm{M}}^2}}  = \sqrt {{{\rm{a}}^2} + {{\left( {\frac{{3{\rm{a}}}}{2}} \right)}^2}}  = \frac{{{\rm{a}}\sqrt {13} }}{2}\)

Ví dụ 6: Cho tam giác đều ABC cạnh a và G là trọng tâm. Gọi I là trung điểm của AG. Tính độ dài của các vécto \(\overrightarrow {{\rm{AG}}} ,\overrightarrow {{\rm{BI}}} \).

Giải

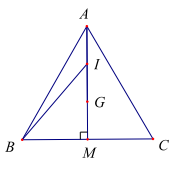
Ta có \(|\overrightarrow {{\rm{AG}}} | = {\rm{AG}} = \frac{2}{3}{\rm{AM}} = \frac{2}{3}\sqrt {{\rm{A}}{{\rm{B}}^2} - {\rm{B}}{{\rm{M}}^2}}  = \)\[\frac{2}{3}\sqrt {{a^2} - \frac{{{a^2}}}{4}}  = \frac{{a\sqrt 3 }}{3}\]

 \(|\overrightarrow {{\rm{BI}}} | = {\rm{BI}} = \sqrt {{\rm{B}}{{\rm{M}}^2} + {\rm{M}}{{\rm{I}}^2}}  = \sqrt {\frac{{{{\rm{a}}^2}}}{4} + \frac{{{{\rm{a}}^2}}}{3}}  = \frac{{{\rm{a}}\sqrt {21} }}{6}\)

Bài tâp

Bài 1: Cho tam giác ABC có trọng tâm G. Gọi I là trung điểm của C$. Dựng điểm \(B\) ' sao cho \(\overrightarrow {{{\rm{B}}^\prime }{\rm{B}}}  = \overrightarrow {{\rm{AG}}} \)

a) Chứng minh: \(\overrightarrow {{\rm{BI}}}  = \overrightarrow {{\rm{IC}}} \)

b) Gọi J là trung điểm của \({\rm{B}}{{\rm{B}}^\prime }\). Chứng minh : \(\overrightarrow {{\rm{BJ}}}  = \overrightarrow {{\rm{IG}}} \)

Bài 2: Cho hình bình hành ABCD. Gọi M,N lần lượt là trung điểm của DC,AB . Gọi P là giao điểm của của AM và DB ; Q là giao điểm của CN và DB. Chứng minh \(\overrightarrow {{\rm{DP}}}  = \overrightarrow {{\rm{PQ}}}  = \overrightarrow {{\rm{QB}}} \)

Bài 3: Cho hình thang ABCD có hai đáy là AB và CD với \(AB = 2CD\). Từ C vẽ \(\overrightarrow {{\rm{CI}}}  = \overrightarrow {{\rm{DA}}} \). Chứng minh:

a) \(\overrightarrow {{\rm{DI}}}  = \overrightarrow {{\rm{CB}}} \). b) \(\overrightarrow {{\rm{AI}}}  = \overrightarrow {{\rm{IB}}}  = \overrightarrow {{\rm{DC}}} \).

B. Tổng và hiệu hai vécto

Dạng 1: Tìm tổng của hai vecto và tổng của nhiều vécto

Phưong pháp: Dùng định nghĩa tổng của hai véctơ, quy tắc ba điểm, quy tắc hình bình hành và các tính chất của tổng các véctơ

Ví dụ 1: Cho lục giác đều ABCDEF tâm O. Chứng minh \(\overrightarrow {{\rm{OA}}}  + \overrightarrow {{\rm{OB}}}  + \overrightarrow {{\rm{OC}}}  + \overrightarrow {{\rm{OD}}}  + \overrightarrow {{\rm{OE}}}  + \overrightarrow {{\rm{OF}}}  = \vec 0\)

Ví dụ 2: Cho năm điểm A,B,C,D,E. Hãy tính tổng \(\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{BC}}}  + \overrightarrow {{\rm{CD}}}  + \overrightarrow {{\rm{DE}}} \)

Ví dụ 3: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD.

a) Tìm tổng của hai véctơ \(\overrightarrow {{\rm{NC}}} \) và \(\overrightarrow {{\rm{MC}}} ,\overrightarrow {{\rm{AM}}} \) và \(\overrightarrow {{\rm{CD}}} ,\overrightarrow {{\rm{AD}}} \) và \(\overrightarrow {{\rm{NC}}} \).

b) Chứng minh \(\overrightarrow {{\rm{AM}}}  + \overrightarrow {{\rm{AN}}}  = \overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AD}}} \)

Dang 2 : Tìm vecto đối và hiệu của hai vécto

Phương pháp:

1) Tính tổng \(\vec a - \vec b\), ta làm hai bước sau:

- Tìm véctơ đối của \(\vec b\) là \( - \vec b\)

- Tính tổng \(\vec a + ( - \vec b)\)

2) Vận dụng quy tắc \(\overrightarrow {{\rm{OA}}}  - \overrightarrow {{\rm{OB}}}  = \overrightarrow {{\rm{BA}}} \) với ba điểm O,A,B bất kì.

Ví dụ 1: Cho tam giác ABC.Các điểm M, N và P lần lượt là trung điểm củaA B, AC và BC.

a) Tìm hiệu \(\overrightarrow {{\rm{AM}}}  - \overrightarrow {{\rm{AN}}} ,\overrightarrow {{\rm{MN}}}  - \overrightarrow {{\rm{NC}}} ,\overrightarrow {{\rm{MN}}}  - \overrightarrow {{\rm{PN}}} ,\overrightarrow {{\rm{BP}}}  - \overrightarrow {{\rm{CP}}} \)

b) Phân tích \(\overrightarrow {AM} \) theo hai vecto \(\overrightarrow {MN} \) và \(\overrightarrow {MP} \)

Ví dụ 2: Cho bốn điểm A,B,C, A. Chứng minh \(\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{CD}}}  = \overrightarrow {{\rm{AC}}}  - \overrightarrow {{\rm{BD}}} \)

Ví dụ 3: Cho hai điểm phân biệt A và B. Tìm điểm M thoả mãn một trong các điều kiện sau:

a) \(\overrightarrow {{\rm{MA}}}  - \overrightarrow {{\rm{MB}}}  = \overrightarrow {{\rm{BA}}} \)

b) \(\overrightarrow {{\rm{MA}}}  - \overrightarrow {{\rm{MB}}}  = \overrightarrow {{\rm{AB}}} \)

c) \(\overrightarrow {{\rm{MA}}}  + \overrightarrow {{\rm{MB}}}  = \vec 0\)

Dạng 3 : Chúng minh Đẳng thúc vécto

Phương pháp:

Sử dụng quy tắc ba điểm, quy tắc hình bình hành, trung điểm để biến đổi vế này thành vế kia của đẳng thức hoặc biến đổi cả hai vế để được hai vế bằng nhau hoặc ta cũng có thể biến đổi đẳng thức véctơ cần chứng minh đó tương đương với một đẳng thức véctơ đã được công nhận là đúng.

Ví dụ 1: Cho bốn điểm bất kì A,B,C,D. Chứng minh các đẳng thức sau:

a) \(\overrightarrow {{\rm{AC}}}  + \overrightarrow {{\rm{BD}}}  = \overrightarrow {{\rm{AD}}}  + \overrightarrow {{\rm{BC}}} \)

b) \(\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{CD}}}  = \overrightarrow {{\rm{AD}}}  + \overrightarrow {{\rm{CB}}} \)

c) \(\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{CD}}}  = \overrightarrow {{\rm{AC}}}  - \overrightarrow {{\rm{BD}}} \)

Ví dụ 2: Cho 6 điểm A,B,C,D,E,F tuỳ ý . Chứng minh rằng:

\(\overrightarrow {{\rm{AC}}}  + \overrightarrow {{\rm{BD}}}  + \overrightarrow {{\rm{EF}}}  = \overrightarrow {{\rm{AF}}}  + \overrightarrow {{\rm{BC}}}  + \overrightarrow {{\rm{ED}}} \)

Ví dụ 3: Cho hình bình hành ABCD tâm O. Chứng minh :

\(\overrightarrow {{\rm{BD}}}  - \overrightarrow {{\rm{BA}}}  = \overrightarrow {{\rm{OC}}}  - \overrightarrow {{\rm{OB}}} {\rm{ va  }}\overrightarrow {{\rm{BC}}}  - \overrightarrow {{\rm{BD}}}  + \overrightarrow {{\rm{BA}}}  = \vec 0\)

Ví dụ 4: Cho hình bình hành ABCD tâm O. M là điểm tuỳ ý. Chứng minh :

\(\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{OA}}}  = \overrightarrow {{\rm{OB}}} {\rm{ va  }}\overrightarrow {{\rm{MA}}}  + \overrightarrow {{\rm{MC}}}  = \overrightarrow {{\rm{MB}}}  + \overrightarrow {{\rm{MD}}} \)

Ví dụ 5: Cho hình bình hành ABCD. Gọi M và N là trung điểm của AD và BC. Chứng minh

a) \(\overrightarrow {{\rm{AD}}}  + \overrightarrow {{\rm{MB}}}  + \overrightarrow {{\rm{NA}}}  = \vec 0\)

b) \(\overrightarrow {{\rm{CD}}}  - \overrightarrow {{\rm{CA}}}  + \overrightarrow {{\rm{CB}}}  = \vec 0\)

Ví dụ 6: Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:

a) \(\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{CD}}}  = \overrightarrow {{\rm{AD}}}  + \overrightarrow {{\rm{CB}}} \)

b) \(\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{CD}}}  = \overrightarrow {{\rm{AC}}}  + \overrightarrow {{\rm{DB}}} \)

c) \(\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{AD}}}  = \overrightarrow {{\rm{CB}}}  - \overrightarrow {{\rm{CD}}} \)

d) \(\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{BC}}}  + \overrightarrow {{\rm{CD}}}  + \overrightarrow {{\rm{DA}}}  = \vec 0\)

e) \(\overrightarrow {{\rm{AD}}}  + \overrightarrow {{\rm{BE}}}  + \overrightarrow {{\rm{CF}}}  = \overrightarrow {{\rm{AE}}}  + \overrightarrow {{\rm{BF}}}  + \overrightarrow {{\rm{CD}}} \)

f) \(\overrightarrow {{\rm{AC}}}  + \overrightarrow {{\rm{DE}}}  - \overrightarrow {{\rm{DC}}}  - \overrightarrow {{\rm{CE}}}  + \overrightarrow {{\rm{CB}}}  = \overrightarrow {{\rm{AB}}} \)

Dạng 4 : Tính độ dài vécto

Phương pháp: Đưa tổng hoặc hiệu của các véctơ về một véctơ có độ dài là một cạnh của đa giác

Ví dụ 1: Cho tam giác ABC vuông tại A, biết \({\rm{AB}} = {\rm{a}};{\rm{AC}} = 2{\rm{a}}\). Tính \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AC}}} |\) và \(|\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{AC}}} |\).

Giải:

$+|\overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}|=\left|\overrightarrow{\text{AD}}\right|=\text{AD}=\text{BC}=\sqrt{{\text{a}}^2+{\left(2\text{a}\right)}^2}=\text{a}\sqrt{5}$

$+|\overrightarrow{\text{AB}}-\overrightarrow{\text{AC}}|=\left|\overrightarrow{\text{CB}}\right|=\text{CB}=\text{a}\sqrt{5}$

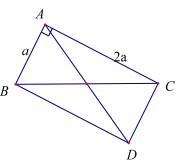
Ví dụ 2: Cho tam giác đều ABC cạnh a. Tính \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{BC}}} |\) và \(|\overrightarrow {{\rm{CA}}}  - \overrightarrow {{\rm{CB}}} |\).

Giải:

$\begin{array}{l}+|\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}|=\left|\overrightarrow{\text{AC}}\right|=\text{AC}=\text{a}\\ +|\overrightarrow{\text{AB}}-\overrightarrow{\text{AC}}|=\left|\overrightarrow{\text{CB}}\right|=\text{CB}=\text{a}\end{array}$

Ví dụ 3: Cho hình thoi ABCD cạnh a có $\text{BAD}={60}^{°}$. Gọi O là giao điểm hai đường chéo .Tính:

a) \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AD}}} |\)

b) \(|\overrightarrow {{\rm{BA}}}  - \overrightarrow {{\rm{BC}}} |\);

c) \(|\overrightarrow {{\rm{OB}}}  - \overrightarrow {{\rm{DC}}} |\)

Giải:

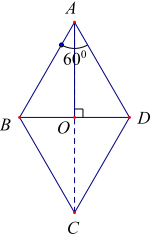
a) \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AD}}} | = |\overrightarrow {{\rm{AC}}} | = {\rm{AC}} = 2{\rm{AO}} = \sqrt {{\rm{A}}{{\rm{B}}^2} - {\rm{B}}{{\rm{O}}^2}}  = {\rm{a}}\sqrt 3 \)

b) \(|\overrightarrow {{\rm{BA}}}  - \overrightarrow {{\rm{BC}}} | = |\overrightarrow {{\rm{CA}}} | = {\rm{CA}} = {\rm{a}}\sqrt 3 \)

c) \(|\overrightarrow {{\rm{OB}}}  - \overrightarrow {{\rm{DC}}} | = |\overrightarrow {{\rm{DO}}}  - \overrightarrow {{\rm{DC}}} | = |\overrightarrow {{\rm{CO}}} | = {\rm{CO}} = \frac{{{\rm{a}}\sqrt 3 }}{2}\)

Ví dụ 4: Cho tam giác ABC vuông tại A, biết AB= a và $\text{B}={60}^{°}$ Tính \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{BC}}} |\) và \(|\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{AC}}} |\).

Giải:

$\begin{array}{l}+|\overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}|=\left|\overrightarrow{\text{AC}}\right|=\text{AC}=\text{AB}\cdot \tan {60}^{°}=a\sqrt{3}\\ +|\overrightarrow{\text{AB}}-\overrightarrow{\text{AC}}|=\left|\overrightarrow{\text{CB}}\right|=\text{CB}=\frac{\text{a}}{\cos {60}^{°}}=2\text{a}\end{array}$

Ví dụ 5: Cho hình vuông ABCD cạnh a, có O là giao điểm hai đường chéo . Tính:

a) \(|\overrightarrow {{\rm{OA}}}  - \overrightarrow {{\rm{CB}}} |\)

b) \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{DC}}} |\);

c) \(|\overrightarrow {{\rm{CD}}}  - \overrightarrow {{\rm{DA}}} |\)

Giải:

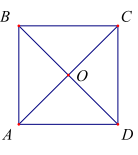
a) \(|\overrightarrow {{\rm{OA}}}  - \overrightarrow {{\rm{CB}}} | = |\overrightarrow {{\rm{CO}}}  - \overrightarrow {{\rm{CB}}} | = |\overrightarrow {{\rm{BO}}} | = {\rm{BO}} = \frac{{{\rm{a}}\sqrt 2 }}{2}\)

b) \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{DC}}} | = |\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AB}}} | = 2|\overrightarrow {{\rm{AB}}} | = 2{\rm{a}}\)

c) \(|\overrightarrow {{\rm{CD}}}  - \overrightarrow {{\rm{DA}}} | = |\overrightarrow {{\rm{CD}}}  - \overrightarrow {{\rm{CB}}} | = |\overrightarrow {{\rm{BD}}} | = {\rm{BD}} = {\rm{a}}\sqrt 2 \)

Bài tâp

Bài 1:Cho tam giác đều ABC cạnh a và đường cao AH.Tính \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AC}}} |\) và \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{BH}}} |,|\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{AC}}} |\).

Bài 2: Cho hình vuông ABCD cạnh a . Tính \(|\overrightarrow {{\rm{BC}}}  + \overrightarrow {{\rm{AB}}} |;|\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{AC}}} |\)

Bài 3: Cho hình chữ nhật ABCD. Gọi O là giao điểm hai đường chéo AC và BD.

a) Với M tuỳ ý, Hãy chứng minh: \(\overrightarrow {{\rm{MA}}}  + \overrightarrow {{\rm{MC}}}  = \overrightarrow {{\rm{MB}}}  + \overrightarrow {{\rm{MD}}} \)

b) Chứng minh rằng: \(|\overrightarrow {{\rm{AB}}}  + \overrightarrow {{\rm{AD}}} | = |\overrightarrow {{\rm{AB}}}  - \overrightarrow {{\rm{AD}}} |\)

Bài 4 : Cho hai véctơ \(\vec a\) và \(\vec b\) cùng khác \(\vec 0\). Khi nào thì:

a) \(|\vec a + \vec b| = |\vec a| + |\vec b|\)

b) \(|\vec a + \vec b| = |\vec a| - |\vec b|\)

c) \(|\vec a - \vec b| = |\vec a| - |\vec b|\)

Bài 5: Tìm tính chất tam giác ABC biết rằng : \(|\overrightarrow {{\rm{CA}}}  + \overrightarrow {{\rm{CB}}} | = |\overrightarrow {{\rm{CA}}}  - \overrightarrow {{\rm{CB}}} |\)