Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 4 Bài 3: Phương trình bậc hai một ẩn. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 3: Phương trình bậc hai một ẩn. Mời các bạn đón xem:
Bài tập Toán 9 Chương 4 Bài 3: Phương trình bậc hai một ẩn
A. Bài tập Phương trình bậc hai một ẩn
I. Bài tập trắc nghiệm
Câu 1: Hệ số c của phương trình x2 + 7x + 9 = 9 là?
A. 9
B. -9
C. 0
D. 18
Lời giải:
Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0 .Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0 .
Khi đó ta có:
Do đó hệ số c là x2 + 7x + 9 = 9 ⇔ x2 + 7x = 0
Chọn đáp án C.
Câu 2: Trong các phương trình sau, phương trình nào là phương trình bậc hai?
A. x2 + 4x - 7 = x2 + 8x - 10
B. x3 + 8x = 0
C. x2 - 4 = 0
D. 5x - 1 = 0
Lời giải:
Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0 .Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0 .
+ x2 + 4x - 7 = x2 + 8x - 10 ⇔ 4x - 3 = 0 . Loại vì đây là phương trình bậc nhất
+ x3 + 8x = 0 vì mũ cao nhất của x là 3 nên không là phương trình bậc hai.
+ x2 - 4 = 0 là phương trình bậc hai thỏa mãn
+ 5x - 1 = 0 là phương trình bậc nhất một ẩn
Chọn đáp án C.
Câu 3: Số nghiệm của phương trình x2 = 20x - 102 là?
A. 1 nghiệm
B. 2 nghiệm
C. Vô số nghiệm
D. Vô nghiệm
Lời giải:
Ta có:
Vậy phương tình đã cho có 1 nghiệm
Chọn đáp án A.
Câu 4: Tập nghiệm của bất phương trình Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án
A. x > -4
B. x < -4
C. x ≤ -4
D. x = -4
Lời giải:
Ta có:
Suy ra x = -4
Chọn đáp án D.
Câu 5: Tập nghiệm của bất phương trình x2 + 10x + 26 < 1
A. x ≥ -5
B. x ≤ -5
C. x = -5
D. Vô nghiệm
Lời giải:
Ta có:
Bất phương trình vô nghiệm vì
Chọn đáp án D.
Câu 6: Cho phương trình 2x2 – 10x + 100 = -2x + 10. Sau khi đưa phương trình trên về dạng ax2 + bx + c = 0 thì hệ số b là?
A. -8
B . -12
C. 12
D. 8
Lời giải:
Ta có:
2x2 – 10x + 100 = -2x + 10
⇔ 2x2 – 10x +100 + 2x -10 =0
⇔ 2x2 – 8x + 90 = 0
Đây là phương trình bậc hai một ẩn có a = 2; b = - 8 và c = 90 .
Chọn đáp án A.
Câu 7: Cho phương trình 2x3 + 2x2 - 3x + 10 = 2x3 + x2 – 10. Sau khi biến đổi đưa phương trình trên về dạng ax2 + bx+ c =0 thì hệ số a bằng ?
A. 2
B.1
C. 3
D. -1
Lời giải:
Ta có : 2x3 + 2x2 - 3x + 10 = 2x3 + x2 – 10
⇔ 2x3 + 2x2 - 3x + 10 - 2x3 - x2 + 10= 0
⇔ x2 – 3x + 20 = 0
Phương trình trên là phương trình bậc hai một ẩn với a = 1; b = -3 và c = 20.
Chọn đáp án B.
Câu 8: Giải phương trình sau: 2x2 - 5x + 3 = 0
Chọn đáp án D.
Câu 9: Giải phương trình -10x2 + 40 = 0
A. Vô nghiệm
B. x = 2
C. x = 4
D . x = ±2
Ta có: -10x2 + 40 = 0
⇔ -10x2 = - 40 ⇔ x 2 = 4
⇔ x = ±2
Chọn đáp án C.
Câu 10: Giải phương trình x2 - 10x + 8 = 0
Ta có:
Chọn đáp án A.
Câu 11: Tìm tích các giá trị của m để phương trình 4mx2 − x – 14m2 = 0 có nghiệm x = 2
Thay x = 2 vào phương trình 4mx2 – x – 10m2 = 0, ta có:
Đáp án cần chọn là: A
Câu 12: Tìm tổng các giá trị của m để phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0 có nghiệm x = −3
A. −5
B. −4
C. 4
D. 6
Thay x = −3 vào phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là: B
Câu 13: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: 9x2 − 15x + 3 = 0
A. ∆ = 117 và phương trình có nghiệm kép
B. ∆ = − 117 và phương trình vô nghiệm
C. ∆ = 117 và phương trình có hai nghiệm phân biệt
D. ∆ = − 117 và phương trình có hai nghiệm phân biệt
Ta có: 9x2 − 15x + 3 = 0 (a = 9; b = −15; c = 3)
⇒ ∆ = b2 – 4ac = (−15)2 – 4.9.3 = 117 > 0 nên phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: C
Câu 14: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: −13x2 + 22x − 13 = 0
A. ∆ = 654 và phương trình có nghiệm kép
B. ∆ = −192 và phương trình vô nghiệm
C. ∆ = − 654 và phương trình vô nghiệm
D. ∆ = − 654 và phương trình có hai nghiệm phân biệt
Ta có:
−13x2 + 22x − 13 = 0 (a = −13; b = 22; x = −13)
⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0 nên phương trình vô nghiệm
Đáp án cần chọn là: B
Câu 15: Tính biệt thức ∆ từ đó tìm các nghiệm (nếu có) của phương trình 
A. ∆ = 0 và phương trình có nghiệm kép x1 = x2 = √2
B. ∆ < 0 và phương trình vô nghiệm
C. ∆ = 0 và phương trình có nghiệm kép x1 = x2 = −√2
D. ∆ > 0 và phương trình có hai nghiệm phân biệt x1 = −√2 ; x2 =√2
nên phương trình có nghiệm kép
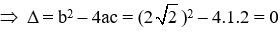
Đáp án cần chọn là: A
II. Bài tập tự luận có lời giải
Câu 1: Giải phương trình x2 - 3x = 0
Lời giải:
Ta có: x2 - 3x = 0 ⇔ x(x - 3) = 0
Vậy phương trình có hai nghiệm là x1 = 0; x2 = 3
Câu 2: Đưa các phương trình sau về dạng ax2 + bx + c = 0 rồi chỉ rõ các hệ số a, b, c của phương trình ấy. Các phương trình: 5x2 - 3x = 10x + 100; x2 = 900
Lời giải:
+ Ta có: 5x2 - 3x = 10x + 100 ⇔ 5x2 - 13x - 100 = 0
Hệ số a = 5; b = -13; c = -100
+ Ta có: x2 = 900 ⇔ x2 - 900 = 0
Hệ số a = 1, b = 0; c = -900
Câu 3: Giải các phương trình sau bằng cách thêm bớt thích hợp
a) x2 + 6x = -8
b) x2 + x = 7
Lời giải:
a) Ta có: x2 + 6x = -8 ⇔ x2 + 6x + 9 = -8 + 9
⇔ (x + 3)2 = 1 
Vậy phương trình đã cho có x = -2 hoặc x = -4
b) Ta có: 
Vậy phương trình đã cho có nghiệm là 
III. Bài tập vận dụng
Câu 1: Giải phương trình bằng cách phân tích đa thức thành nhân tử x2 - 7x + 12 = 0
Câu 2: Giải phương trình 
B. Lý thuyết Phương trình bậc hai một ẩn
1. Định nghĩa
Phương trình bậc hai một ẩn là phương trình có dạng: ax2 + bx + c = 0. Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.
Ví dụ:
+ x2 - 5x + 4 = 0 là phương trình bậc hai một ẩn trong đó a = 1; b = -5; c = 4
+ 2x2 - 13x + 17 = 0 là phương trình bậc hai một ẩn trong đó a = -2; b = -13; c = 17.
+ x2 – 10 = 0 là phương trình bậc hai một ẩn có a = 1; b = 0 và c = -10
+ x2 + 20x = 0 là phương trình bậc hai một ẩn có a = 1 và b = 20; c = 0
2. Giải phương trình với hai trường hợp đặc biệt
a) Trường hợp c = 0.
Khi đó phương trình có dạng: ax2 + bx = 0 ⇔ x(ax + b) = 0
Phương trình có nghiệm: x1 = 0; x2 = -b/a
Ví dụ: Giải phương trình x2 - 3x = 0
Ta có: x2 - 3x = 0 ⇔ x(x - 3) = 0
Vậy phương trình có hai nghiệm là x1 = 0; x2 = 3
b) Trường hợp b = 0
Khi đó phương trình có dạng: ax2 + c = 0 ⇔ x2 = -c/a
+ Nếu a, c cùng dấu thì -c/a < 0 ⇒ phương trình vô nghiệm.
+ Nếu a, c khác dấu thì -c/a > 0 ⇒ phương trình có hai nghiệm
Ví dụ: Giải phương trình 2x2 - 3 = 0.
Ta có:
Vậy phương trình có hai nghiệm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
