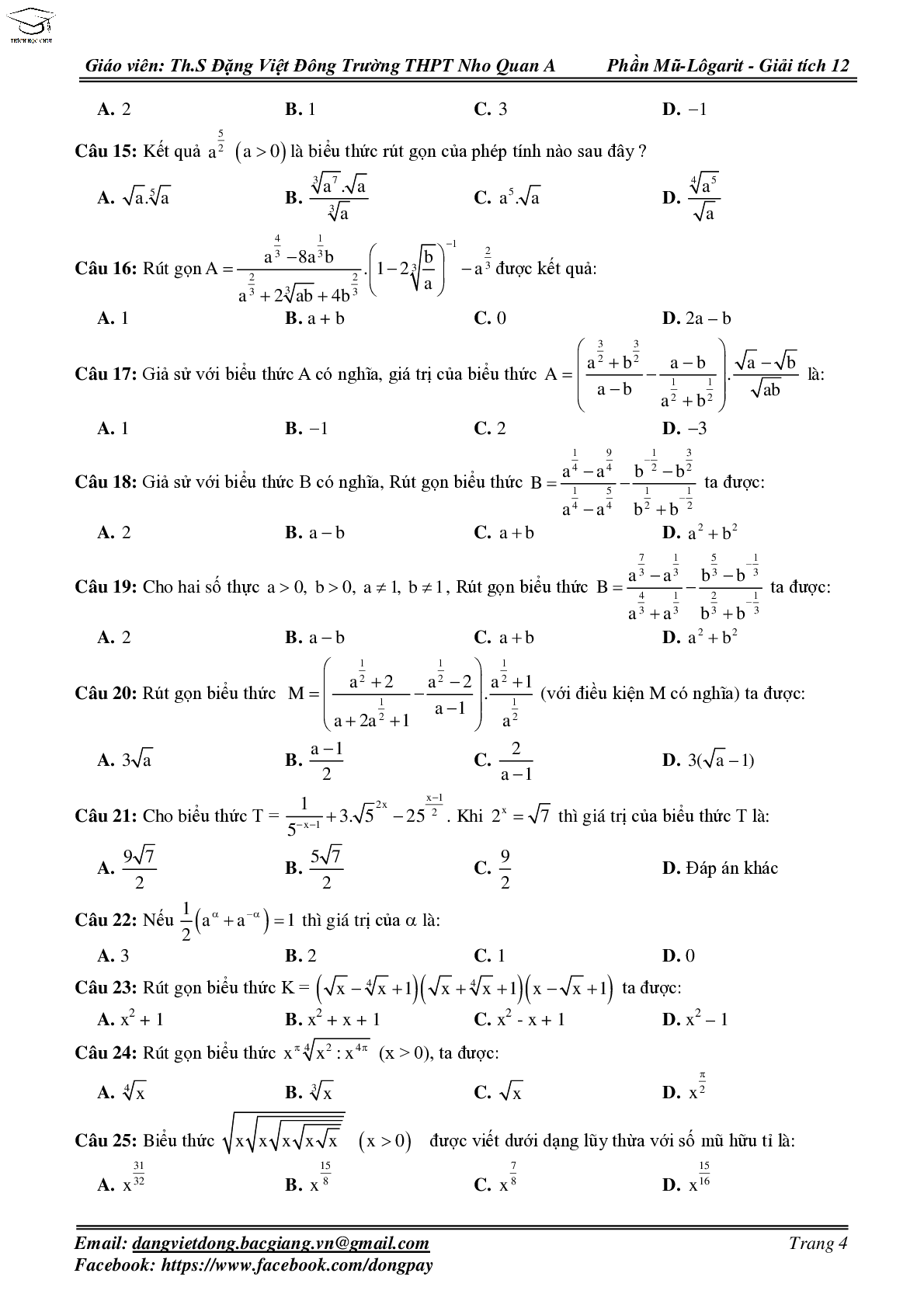Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn bài tập trắc nghiệm Chuyên đề Mũ - Lôgarit, tài liệu bao gồm 63 trang. Đề thi được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi TN THPT. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lũy thừa

A. Lý thuyết tóm tắt

1. Định nghĩa lũy thừa

2. Tính chất của lũy thừa

* Với mọi a > 0, b > 0 ta có:

\[\begin{array}{l}{a^\alpha }.{a^\beta } = {a^{\alpha  + \beta }};\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha  - \beta }};\\{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha .\beta }};{\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha };\\{\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\end{array}\]

* a > 1: \[{a^\alpha } > {a^\beta } \Leftrightarrow \alpha  > \beta \]

0 < a < 1: \[{a^\alpha } > {a^\beta } \Leftrightarrow \alpha  < \beta \]

* Với 0 < a < b ta có:

\[{a^m} < {b^m} \Leftrightarrow m > 0\]           

\[{a^m} > {b^m} \Leftrightarrow m < 0\]

Chú ý:

+ Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

+ Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.

3. Định nghĩa và tính chất của căn thức

* Căn bậc n của a là số b sao cho bⁿ = a

* Với \[a,b \ge 0,m,n \in N*,p,q \in Z\] ta có:

\[\sqrt[n]{{ab}} = \sqrt[n]{a}.\sqrt[n]{b};\sqrt[n]{{\frac{a}{b}}} = \frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}}\left( {b > 0} \right)\]

\[\sqrt[n]{{{a^p}}} = {\left( {\sqrt[n]{a}} \right)^p}\left( {a > 0} \right)\]                    \[\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}\]

Nếu \[\frac{p}{n} = \frac{q}{m}\] thì \[\sqrt[n]{{{a^p}}} = \sqrt[m]{{{a^q}}}\left( {a > 0} \right)\]. Đặc điệt \[\sqrt[n]{a} = \sqrt[{mn}]{{{a^m}}}\]

* Nếu n là số nguyên dương lẻ và a < b thì \[\sqrt[n]{a} < \sqrt[n]{b}\]

  Nếu n là số nguyên dương chẵn và 0 < a < b thì \[\sqrt[n]{a} < \sqrt[n]{b}\]

Chú ý:

+ Khi n lẻ, mỗi số thực a chỉ có mật căn bậc n. Kí hiệu \[\sqrt[n]{a}\]

+ Khi n chẵn, mỗi số thực dương a có đúng hai căn bậc n là hai số đối nhau

B. Bài tập

Câu 1. Cho x, y là hai số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?

A. \[{x^m}.{x^n} = {x^{m + n}}\]

B. \[{\left( {xy} \right)^n} = {x^n}.{y^n}\]

C. \[{\left( {{x^n}} \right)^m} = {x^{nm}}\]

D. \[{x^m}.{y^n} = {\left( {xy} \right)^{m + n}}\]

Câu 2. Nếu m là số nguyên dương, biểu thức nào theo sau đây không bằng với (2⁴)^m?

A. \[{4^{2m}}\]

B. \[{2^m}.\left( {{2^{3m}}} \right)\]

C. \[{4^m}.\left( {{2^m}} \right)\]

D. \[{2^{4m}}\]

Câu 3. Giá trị của biểu thức \[A = {9^{2 + 3\sqrt 3 }}:{27^{2\sqrt 3 }}\] là:

A. 9

B. \[{3^{4 + 5\sqrt 3 }}\]

C. 81

D. \[{3^{4 + 12\sqrt 3 }}\]

Câu 4. Giá trị của biểu thức \[A = \frac{{{2^3}{{.2}^{ - 1}} + {5^{ - 3}}{{.5}^4}}}{{{{10}^{ - 3}}:{{10}^{ - 2}} - {{\left( {0,1} \right)}^0}}}\] là:

A. – 9

B. 9

C. – 10

D. 10

Câu 5. Tính \[{\left( { - 0,5} \right)^{ - 4}} - {625^{0,25}} - {\left( {2\frac{1}{4}} \right)^{ - 1\frac{1}{2}}} + 19.{\left( { - 3} \right)^{ - 3}}\] kết quả là:

A. 10

B. 11

C. 12

D. 13

Câu 6. Giá trị của biểu thức \[A = \frac{{\left( {{2^{2\sqrt 3 }} - 1} \right)\left( {{2^{\sqrt 3 }} + {2^{2\sqrt 3 }} + {2^{2\sqrt 3 }}} \right)}}{{{2^{4\sqrt 3 }} - {2^{\sqrt 3 }}}}\] là:

A. 1

B. \[{2^{\sqrt 3 }} + 1\]

C. \[{2^{\sqrt 3 }} - 1\]

D. – 1

Câu 7. Tính: \[0,{001^{ - \frac{1}{3}}} - {\left( { - 2} \right)^{ - 2}}{.64^{\frac{3}{2}}} - {8^{ - 1\frac{1}{3}}} + {\left( {{9^0}} \right)^2}\] kết quả là:

A. \[\frac{{115}}{{16}}\]

B.  \[\frac{{109}}{{16}}\]

C. \[ - \frac{{1873}}{{16}}\]

D.  Đáp án khác

Câu 8. Tính: \[{81^{ - 0,75}} + {\left( {\frac{1}{{125}}} \right)^{ - \frac{1}{3}}} - {\left( { - \frac{1}{{32}}} \right)^{ - \frac{3}{5}}}\] kết quả là:

A. \[ - \frac{{80}}{{27}}\]

B. \[\frac{{352}}{{27}}\]

C. \[\frac{{80}}{{27}}\]

D. Đáp án khác

Câu 9. Trục căn thức ở mẫu biểu thức \[\frac{1}{{\sqrt[3]{5} - \sqrt[3]{2}}}\] ta được:

A. \[\frac{{\sqrt[3]{{25}} + \sqrt[3]{{10}} + \sqrt[3]{4}}}{3}\]

B. \[\sqrt[3]{5} + \sqrt[3]{2}\]

C. \[\sqrt[3]{{75}} + \sqrt[3]{{15}} + \sqrt[3]{4}\]

D. \[\sqrt[3]{5} + \sqrt[3]{4}\]

Câu 10. Rút gọn: \[\frac{{{{\left( {\sqrt[4]{{{a^3}.{b^2}}}} \right)}^4}}}{{\sqrt[3]{{\sqrt {{a^{12}}.{b^6}} }}}}\] ta được:

A. a²b

B. ab²

C. a²b²

D. Ab

Câu 11. Rút gọn: \[\left( {{a^{\frac{2}{3}}} + 1} \right)\left( {{a^{\frac{4}{9}}} + {a^{\frac{2}{9}}} + 1} \right)\left( {{a^{\frac{2}{9}}} - 1} \right)\] ta được:

A. \[{a^{\frac{1}{3}}} + 1\]

B. \[{a^{\frac{4}{3}}} + 1\]

C. \[{a^{\frac{4}{3}}} - 1\]

D. \[{a^{\frac{1}{3}}} - 1\]

Câu 12. Rút gọn: \[{a^{ - 2\sqrt 2 }}.{\left( {\frac{1}{{{a^{ - \sqrt 2  - 1}}}}} \right)^{\sqrt 2  + 1}}\] ta được:

A. a³

B. a²

C. a

D. a⁴

Câu 13. Với giá trị thực nào của a thì \[\sqrt {a.\sqrt[3]{{a.\sqrt[4]{a}}}}  = \sqrt[{24}]{{{2^5}}}.\frac{1}{{\sqrt {{2^{ - 1}}} }}\]?

A. a = 0

B. a = 1

C. a = 2

D. a = 3

Câu 14. Rút gọn biểu thức \[T = \left( {\frac{{a + b}}{{\sqrt[3]{a} + \sqrt[3]{b}}} - \sqrt[3]{{ab}}} \right):\left( {\sqrt[3]{a} - \sqrt[3]{b}} \right)\]?

A. 2

B. 1

C. 3

D. – 1

Câu 15. Kết quả \[{a^{\frac{5}{2}}}\] (a > 0) là biểu thức rút gọn của phép tính nào sau đây?

A. \[\sqrt a \sqrt[5]{a}\]

B. \[\frac{{\sqrt[3]{{{a^7}}}\sqrt a }}{{\sqrt[3]{a}}}\]

C. \[{a^5}.\sqrt a \]

D. \[\frac{{\sqrt[4]{{{a^5}}}}}{{\sqrt a }}\]

Câu 16. Rút gọn \[A = \frac{{{a^{\frac{4}{3}}} - 8{a^{\frac{1}{3}}}b}}{{{a^{\frac{2}{3}}} + 2\sqrt[3]{{ab}} + 4{b^{\frac{2}{3}}}}}.{\left( {1 - 2\sqrt[3]{{\frac{b}{a}}}} \right)^{ - 1}} - {a^{\frac{2}{3}}}\] được kết quả:

A. 1

B. a + b

C. 0

D. 2a – b

Câu 17. Giả sử với biểu thức A có nghĩa, giá trị của biểu thức \[A = \left( {\frac{{{a^{\frac{3}{2}}} + {b^{\frac{3}{2}}}}}{{a - b}} - \frac{{a - b}}{{{a^{\frac{1}{2}}} + {b^{\frac{1}{2}}}}}} \right).\frac{{\sqrt a  - \sqrt b }}{{\sqrt {ab} }}\] là:

A. 1

B. – 1

C. 2

D. – 3

Câu 18. Giả sử với biểu thức B có nghĩa, Rút gọn biểu thức \[B = \frac{{{a^{\frac{1}{4}}} - {a^{\frac{9}{4}}}}}{{{a^{\frac{1}{4}}} - {a^{\frac{5}{4}}}}} - \frac{{{b^{ - \frac{1}{2}}} - {b^{\frac{3}{2}}}}}{{{b^{\frac{1}{2}}} + {b^{ - \frac{1}{2}}}}}\] ta được:

A. 2

B. a – b

C. a + b

D. a² + b²

Câu 19. Cho hai số thực \[a > 0,b > 0,a \ne 1,b \ne 1\], Rút gọn biểu thức \[B = \frac{{{a^{\frac{7}{3}}} - {a^{\frac{1}{3}}}}}{{{a^{\frac{4}{3}}} + {a^{\frac{1}{3}}}}} - \frac{{{b^{\frac{5}{3}}} - {b^{ - \frac{1}{3}}}}}{{{b^{\frac{2}{3}}} + {b^{\frac{1}{3}}}}}\]

A. 2

B. a – b

C. a + b

D. a² + b²

Câu 20. Rút gọn biểu thức \[M = \left( {\frac{{{a^{\frac{1}{2}}} + 2}}{{a + 2{a^{\frac{1}{2}}} + 1}} - \frac{{{a^{\frac{1}{2}}} - 2}}{{a - 1}}} \right).\frac{{{a^{\frac{1}{2}}} + 1}}{{{a^{\frac{1}{2}}}}}\]( với điều kiện M có nghĩa) ta được:

A. \[3\sqrt a \]

B. \[\frac{{a - 1}}{2}\]

C. \[\frac{2}{{a - 1}}\]

D. \[3\left( {\sqrt a  - 1} \right)\]

Câu 21. Cho biểu thức \[T = \frac{1}{{{5^{ - x - 1}}}} + 3.{\sqrt 5 ^{2x}} - {25^{\frac{{x - 1}}{2}}}\]. Khi \[{2^x} = \sqrt 7 \] thì giá trị của biểu thức T là:

A. \[\frac{{9\sqrt 7 }}{2}\]

B. \[\frac{{5\sqrt 7 }}{2}\]

C. \[\frac{9}{2}\]

D. Đáp án khác

Câu 22. Nếu \[\frac{1}{2}\left( {{a^\alpha } + {a^{ - \alpha }}} \right) = 1\] thì giá trị của α là:

A. 3

B. 2

C. 1

D. 0

Câu 23. Rút gọn biểu thức \[K = \left( {\sqrt x  - \sqrt[4]{x} + 1} \right)\left( {\sqrt x  + \sqrt[4]{x} + 1} \right)\left( {x - \sqrt x  + 1} \right)\] ta được:

A. \[{x^2} + 1\]

B. \[{x^2} + x + 1\]

C. \[{x^2} - x + 1\]

D. \[{x^2} - 1\]

Câu 24. Rút gọn biểu thức \[{x^\pi }\sqrt[4]{{{x^2}:{x^{4\pi }}}}\left( {x > 0} \right)\], ta được:

A. \[\sqrt[4]{x}\]

B. \[\sqrt[3]{x}\]

C. \[\sqrt x \]

D. \[{x^{\frac{\pi }{2}}}\]

Câu 25. Biểu thức \[\sqrt {x\sqrt {x\sqrt {x\sqrt {x\sqrt x } } } } \left( {x > 0} \right)\] được viết dưới dạng lũy thừa với số mũ hữu tỉ là:

A. \[{x^{\frac{{31}}{{32}}}}\]

B. \[{x^{\frac{{15}}{8}}}\]

C. \[{x^{\frac{7}{8}}}\]

D. \[{x^{\frac{{15}}{{16}}}}\]

Câu 26. Rút gọn biểu thức: \[A = \sqrt {x\sqrt {x\sqrt {x\sqrt x } } } :{x^{\frac{{11}}{{16}}}},\left( {x > 0} \right)\] ta được:

A. \[\sqrt[8]{x}\]

B. \[\sqrt[6]{x}\]

C. \[\sqrt[4]{x}\]

D. \[\sqrt x \]

Câu 27. Cho \[f\left( x \right) = \frac{{\sqrt x \sqrt[3]{{{x^2}}}}}{{\sqrt[6]{x}}}\]. Khi đó \[f\left( {\frac{{13}}{{10}}} \right)\] bằng:

A. 1

B. \[\frac{{11}}{{10}}\]

C. \[\frac{{13}}{{10}}\]

D. 4

Câu 28. Mệnh đề nào sau đây là đúng?

A. \[{\left( {\sqrt 3  - \sqrt 2 } \right)^4} < {\left( {\sqrt 3  - \sqrt 2 } \right)^5}\]

B. \[{\left( {\sqrt {11}  - \sqrt 2 } \right)^6} < {\left( {\sqrt {11}  - \sqrt 2 } \right)^7}\]

C. \[{\left( {2 - \sqrt 2 } \right)^3} < {\left( {2 - \sqrt 2 } \right)^4}\]

D.  \[{\left( {4 - \sqrt 2 } \right)^3} < {\left( {4 - \sqrt 2 } \right)^4}\]

Câu 29. Các kết luận sau, kết luận nào sai

I. \[\sqrt {17}  > \sqrt[3]{{28}}\]

II. \[{\left( {\frac{1}{3}} \right)^{\sqrt 3 }} > {\left( {\frac{1}{2}} \right)^{\sqrt 2 }}\]

III. \[{4^{\sqrt 5 }} < {4^{\sqrt 7 }}\]

IV. \[\sqrt[4]{{13}} < \sqrt[5]{{23}}\]

A. II và III

B. III

C. I

D. II và IV

Câu 30. Cho a > 1. Mệnh đề nào sau đây là đúng?

A. \[{a^{ - \sqrt 3 }} > \frac{1}{{{a^{\sqrt 5 }}}}\]

B. \[{a^{\frac{1}{3}}} > \sqrt a \]

C. \[\frac{1}{{{a^{2016}}}} < \frac{1}{{{a^{2017}}}}\]

D.  \[\frac{{\sqrt[3]{{{a^2}}}}}{a} > 1\]

Câu 31. Cho a, b > 0 thỏa mãn: \[{a^{\frac{1}{2}}} > {a^{\frac{1}{3}}},{b^{\frac{2}{3}}} > {b^{\frac{3}{4}}},\]. Khi đó:

A. a > 1, b > 1

B. a > 1, 0 < b < 1

C. 0 < a < 1, b > 1

D. 0 < a < 1, 0 < b < 1

Câu 32. Biết \[{\left( {a - 1} \right)^{ - 2\sqrt 3 }} > {\left( {a - 1} \right)^{ - 3\sqrt 2 }}\]. Khi đó ta có thể kết luận về a là:

A. a > 2

B. a > 1

C. 1 < a < 2

D. 0 < a < 1

Câu 33. Cho 2 số thực a, b thỏa mãn \[a > 0,a \ne 1,b > 0,b \ne 1\]. Chọn đáp án đúng

A. \[{a^m} > {a^n} \Leftrightarrow m > n\]

B. \[{a^m} < {a^n} \Leftrightarrow m < n\]

C. \[\left\{ {\begin{array}{*{20}{c}}{a < b}\\{n > 0}\end{array}} \right. \Rightarrow {a^n} < {b^n}\]

D.  \[\left\{ {\begin{array}{*{20}{c}}{a < b}\\{n < 0}\end{array}} \right. \Rightarrow {a^n} < {b^n}\]

Câu 34. Biết \[{2^{ - x}} + {2^x} = m\] với m ≥ 2. Tính giá trị của \[M = {4^x} + {4^{ - x}}\]:

A. M = m + 2

B. M = m – 2

C. M = m² – 2

D. M = m² + 2

Đáp án

1D, 2C, 3C, 4C, 5A, 6B, 7C, 8D, 9A, 10D, 11C, 12A, 13C, 14B, 15B, 16C, 17A, 18C, 19B, 20C, 21D, 22D, 23B, 24C, 25A, 26C, 27C, 28D, 29D, 30A, 31B, 32A, 33C, 34C