Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 10 Bài 2: Hàm số bậc hai sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 10.
Trắc nghiệm Toán 10 Bài 2: Hàm số bậc hai
I. Nhận biết
Câu 1. Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ:
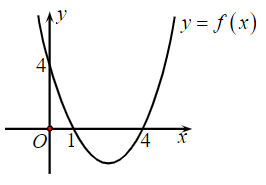
Đặt ∆ = b2 – 4ac. Tìm dấu của a và ∆.
A. a > 0, ∆ > 0;
B. a < 0, ∆ > 0;
C. a > 0, ∆ = 0;
D. a < 0, ∆ = 0.
Hướng dẫn giải
Đáp án: A
Giải thích:
Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.
Lại có đồ thị cắt trục Ox tại hai điểm phân biệt (cụ thể là tại x = 1 và x = 4) nên phương trình ax2 + bx + c = 0 có hai nghiệm x1, x2.
Do đó ∆ > 0.
Vậy a > 0, ∆ > 0.
Do đó ta chọn phương án A.
Câu 2. Cho hàm số y = –x2 + 5x – 4. Khẳng định nào sau đây đúng?
A. Hàm số đạt giá trị lớn nhất bằng
B. Hàm số đạt giá trị nhỏ nhất bằng
C. Hàm số đạt giá trị nhỏ nhất bằng
D. Hàm số đạt giá trị lớn nhất bằng
Hướng dẫn giải
Đáp án: D
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 5, c = –4.
∆ = b2 – 4ac = 52 – 4.(–1).(–4) = 9.
Vì a = –1 < 0 nên hàm số đạt giá trị lớn nhất bằng tại
Vậy hàm số đạt giá trị lớn nhất bằng tại x =
Ta chọn phương án D.
Câu 3. Cho hàm số y = f(x) = x2 + 3x + 4. Bảng giá trị của hàm số đã cho là:
|
x |
–3 |
–2 |
|
–1 |
0 |
|
f(x) |
8 |
2 |
1 |
2 |
8 |
|
x |
–3 |
–2 |
|
–1 |
0 |
|
f(x) |
4 |
6 |
5 |
4 |
6 |
|
x |
–3 |
–2 |
|
–1 |
0 |
|
f(x) |
4 |
2 |
|
2 |
4 |
|
x |
–3 |
–2 |
|
–1 |
0 |
|
f(x) |
2 |
4 |
|
2 |
4 |
Đáp án: C
Giải thích:
Xét hàm số y = f(x) = x2 + 3x + 4.
• Với x = –3, ta có f(–3) = (–3)2 + 3.(–3) + 4 = 4.
• Với x = –2, ta có f(–2) = (–2)2 + 3.(–2) + 4 = 2.
• Với x = , ta có
• Với x = –1, ta có f(–1) = (–1)2 + 3.(–1) + 4 = 2.
• Với x = 0, ta có f(0) = 02 + 3.0 + 4 = 4.
Vậy bảng giá trị của hàm số đã cho là:
|
x |
–3 |
–2 |
|
–1 |
0 |
|
f(x) |
4 |
2 |
2 |
4 |
Do đó ta chọn đáp án C.
Câu 4. Trong các hàm số sau đây, hàm số nào là hàm số bậc hai?
A. f(x) = 3x2 + 2x – 5;
B. f(x) = 2x – 4;
C. f(x) = 3x3 + 2x – 1;
D. f(x) = x4 – x2 + 1.
Hướng dẫn giải
Đáp án: A
Giải thích:
Hàm số bậc hai có dạng y = ax2 + bx + c, với a ≠ 0.
Ta thấy hàm số ở phương án A có dạng như trên với a = 3, b = 2 và c = –5; nên hàm số ở phương án A là hàm số bậc hai.
Hàm số ở phương án B có dạng y = ax + b nên đây là hàm số bậc nhất.
Hàm số ở phương án C có chứa x3 nên đây không phải hàm số bậc hai.
Hàm số ở phương án D có chứa x4 nên đây không phải hàm số bậc hai.
Vậy ta chọn phương án A.
Câu 5. Cho hàm số y = x2 – 2x có đồ thị (P). Khi đó, tọa độ đỉnh của (P) là:
A. (0; 0);
B. (1; –1);
C. (–1; 3);
D. (2; 0).
Hướng dẫn giải
Đáp án: B
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = 1, b = –2, c = 0.
∆ = b2 – 4ac = (–2)2 – 4.1.0 = 4.
Đỉnh S có tọa độ:
⦁
⦁
Suy ra tọa độ đỉnh S(1; –1).
Vậy ta chọn phương án B.
Câu 6. Trục đối xứng của parabol y = –x2 + 5x + 3 là đường thẳng có phương trình:
A.
B.
C.
D.
Hướng dẫn giải
Đáp án: D
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 5, c = 3.
Trục đối xứng của hàm số đã cho là đường thẳng (đường thẳng này đi qua đỉnh S và song song với trục Oy).
Vậy ta chọn phương án D.
Câu 7. Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình bên:
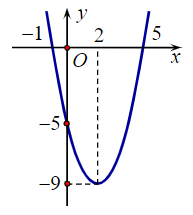
Trục đối xứng của đồ thị hàm số trên là đường thẳng:
A. x = –9;
B. x = –5;
C. x = 0;
D. x = 2.
Hướng dẫn giải
Đáp án: D
Giải thích:
Quan sát đồ thị, ta thấy tọa độ đỉnh S(2; –9).
Trục đối xứng của đồ thị hàm số đã cho là đường thẳng đi qua đỉnh S và song song (hoặc trùng) với trục Oy.
Khi đó trục đối xứng là đường thẳng x = 2.
Vậy ta chọn phương án D.
II. Thông hiểu
Câu 1. Cho hàm số f(x) = x2 – 4x + 5. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (–∞; 2) và đồng biến trên (2; +∞);
B. Hàm số nghịch biến trên (–∞; 2) và (2; +∞);
C. Hàm số đồng biến trên (–∞; 2) và nghịch biến trên (2; +∞);
D. Hàm số đồng biến trên (–∞; 2) và (2; +∞).
Hướng dẫn giải
Đáp án: A
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = 1, b = –4, c = 5.
Ta có:
Vì a = 1 > 0 nên ta có hàm số đã cho nghịch biến trên (–∞; 2) và đồng biến trên (2; +∞).
Vậy ta chọn phương án A.
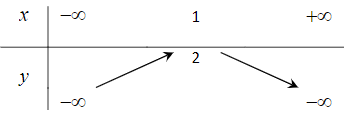
Câu 2. Bảng biến thiên nào dưới đây là của hàm số y = –x2 + 2x + 1?
A. 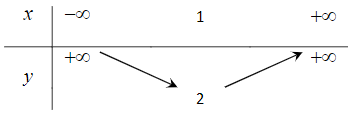
B. 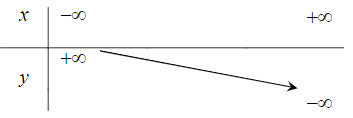
C. 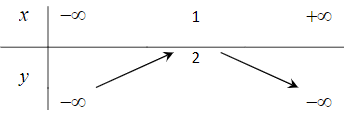
D. 
Hướng dẫn giải
Đáp án: C
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 1.
Đỉnh S có tọa độ:
⦁
⦁ yS = –12 + 2.1 + 1 = 2.
Suy ra S(1; 2).
Vì hàm số bậc hai có a = –1 < 0 nên hàm số đã cho đồng biến trên khoảng (–∞; 1) và nghịch biến trên khoảng (1; +∞).
Ta có bảng biến thiên như sau:
Vậy ta chọn phương án C.
Câu 3. Hàm số y = –x2 + 2x + 3 có đồ thị là hình nào trong các hình sau?
A. 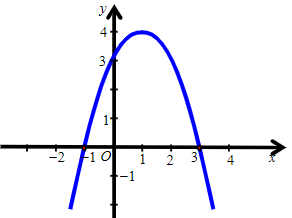
B. 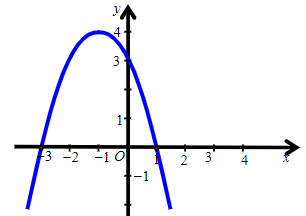
C. 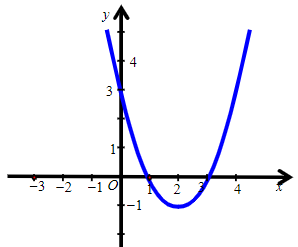
D. 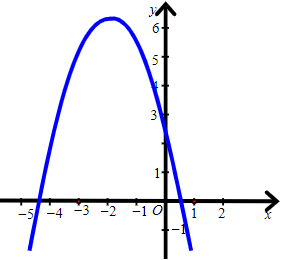
Hướng dẫn giải
Đáp án: A
Giải thích:
Cách 1:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = –1, b = 2, c = 3.
Ta có ∆ = b2 – 4ac = 4 – 4.(–1).3 = 16.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 2x + 3 là một parabol (P):
⦁ Đỉnh S có tọa độ: và
Suy ra tọa độ đỉnh S(1; 4).
⦁ Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy).
⦁ Có bề lõm quay xuống dưới vì a = –1 < 0.
⦁ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ngoài ra, phương trình –x2 + 2x + 3 = 0 có hai nghiệm phân biệt x1 = 3 và x2 = –1 nên đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có tọa độ (3; 0) và (–1; 0).
Ta vẽ được đồ thị sau:
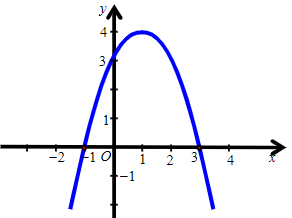
Vậy ta chọn phương án A.
Cách 2:
• Xét hàm số y = –x2 + 2x + 3 có a = –1, b = 2, c = 3.
Vì a = –1 < 0 nên đồ thị có bề lõm quay xuống dưới.
Do đó ta loại phương án C.
• Đỉnh S có tọa độ: và
Suy ra tọa độ đỉnh S(1; 4).
Do đó ta loại phương án B và D.
Vậy ta chọn phương án A.
Câu 4. Cho hàm số y = 2x2 – 4x + 3 có đồ thị là parabol (P). Mệnh đề nào sau đây sai?
A. (P) không có giao điểm với trục hoành;
B. (P) có đỉnh là S(1; 1);
C. (P) có trục đối xứng là đường thẳng y = 1;
D. (P) đi qua điểm M(–1; 9).
Hướng dẫn giải
Đáp án: C
Giải thích:
+ Gọi điểm A là giao điểm của parabol (P) và trục hoành.
Suy ra yA = 0.
Vì A ∈ (P) nên (vô nghiệm).
Do đó không có điểm A là giao điểm của parabol (P) và trục hoành.
Vì vậy phương án A đúng.
+ Hàm số đã cho có dạng y = ax2 + bx + c, với a = 2, b = –4, c = 3.
Đỉnh S có tọa độ:
⦁
⦁ yS = 2.12 – 4.1 + 3 = 1.
Suy ra (P) có đỉnh S(1; 1) và có trục đối xứng là x = 1.
Do đó phương án B đúng, C sai.
+ Thay tọa độ điểm M vào hàm số của đồ thị (P) ta được:
9 = 2.(–1)2 – 4.(–1) + 3 (đúng).
Suy ra (P) đi qua điểm M(–1; 9).
Do đó phương án D đúng.
Vậy ta chọn phương án C.
Câu 5. Cho hàm số y = –x2 – x – 1. Tập giá trị của hàm số đã cho là:
A.
B.
C.
D.
Hướng dẫn giải
Đáp án: B
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = b = c = –1.
Ta có ∆ = b2 – 4ac = (–1)2 – 4.(–1).(–1) = –3.
Suy ra
Vì a = –1 < 0 nên hàm số có giá trị lớn nhất bằng và có tập giá trị là
Vậy ta chọn phương án B.
Câu 6. Đồ thị dưới đây là của hàm số nào sau đây?
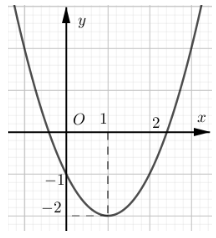
A. y = –x2 – 2x + 3;
B. y = x2 + 2x – 2;
C. y = 2x2 – 4x – 2;
D. y = x2 – 2x – 1.
Hướng dẫn giải
Đáp án: D
Giải thích:
+ Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.
Do đó ta loại phương án A vì a = –1 < 0.
+ Quan sát đồ thị, ta thấy parabol có trục đối xứng là đường thẳng x = 1.
⦁ Ở phương án B, đồ thị của hàm số y = x2 + 2x – 2 có trục đối xứng là đường thẳng
Do đó ta loại phương án B.
⦁ Ở phương án C, đồ thị của hàm số y = 2x2 – 4x – 2 có trục đối xứng là đường thẳng
• Ở phương án D, đồ thị của hàm số y = x2 – 2x – 1 có trục đối xứng là đường thẳng
+ Quan sát đồ thị, ta thấy parabol đi qua điểm A(0; –1).
• Thay x = 0, y = –1 vào hàm số ở phương án C, ta có: –1 = 2.02 – 4.0 – 2 (vô lí).
Do đó đồ thị của hàm số ở phương án C không đi qua điểm A(0; –1).
Vì vậy ta loại phương án C.
• Thay x = 0, y = –1 vào hàm số ở phương án D, ta có –1 = 02 – 2.0 – 1 (đúng).
Do đó đồ thị của hàm số ở phương án D đi qua điểm A(0; –1).
Vậy ta chọn phương án D.
Câu 7. Điều kiện của m để hàm số y = (m – 1)x2 + 2mx – m2 + 4 là hàm số bậc hai là:
A. m > 1;
B. m < 1;
C. m ≠ 1;
D. m ≥ 1.
Hướng dẫn giải
Đáp án: C
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = m – 1, b = 2m, c = –m2 + 4.
Để hàm số đã cho là hàm số bậc hai thì a ≠ 0.
Nghĩa là, m – 1 ≠ 0.
Suy ra m ≠ 1.
Vậy ta chọn phương án C.
Câu 8. Parabol (P): y = ax2 + 3x – 2 (a ≠ 0) có trục đối xứng là đường thẳng x = –3 là:
A. y = x2 + 3x – 2
B.
C.
D.
Hướng dẫn giải
Đáp án: D
Giải thích:
Parabol (P): y = ax2 + 3x – 2 (a ≠ 0) có b = 3.
(P) có trục đối xứng là đường thẳng x = –3.
Ta suy ra
Tức là,
Khi đó ta có a = (thỏa mãn a ≠ 0).
Vậy (P):
Do đó ta chọn phương án D.
III. Vận dụng
Câu 1. Cho hàm số f(x) = ax2 + bx + c (a, b, c ≠ 0) có đồ thị như hình vẽ bên.
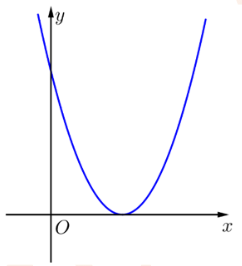
Biết f(c) = c. Giá trị của b là:
A. b = –6;
B. b = –2;
C. ;
D. b = –4.
Hướng dẫn giải
Đáp án: D
Giải thích:
Quan sát đồ thị, ta thấy parabol cắt trục hoành tại đỉnh của parabol hay parabol cắt trục hoành tại một điểm duy nhất.
Nghĩa là, phương trình ax2 + bx + c = 0 có nghiệm kép.
Do đó ∆ = 0.
Suy ra b2 – 4ac = 0 (1)
Ta có f(c) = c.
Suy ra ac2 + bc + c = c.
Khi đó c(ac + b) = 0.
Vì vậy ac + b = 0 (vì c ≠ 0).
Do đó (vì a ≠ 0).
Thay vào (1) ta được:
Khi đó b2 + 4b = 0 b(b + 4) = 0.
Vì vậy b = 0 hoặc b = –4.
Vì b ≠ 0 nên ta nhận b = –4.
Vậy ta chọn phương án D.
Câu 2. Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị đi qua điểm A(0; 6). Giá trị biểu thức P = abc bằng
A. –6;
B. –3;
C. 6;
D.
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có giá trị nhỏ nhất của hàm số bằng 4 tại x = 2.
Tức là đỉnh S(2; 4) và a > 0.
Suy ra 4 = a.22 + b.2 + c.
Do đó 4a + 2b + c = 4 (1)
Ta có xS = 2.
Suy ra
Do đó –b = 4a (2)
Đồ thị hàm số đi qua điểm A(0; 6).
Suy ra 6 = a.02 + b.0 + c.
Do đó c = 6 (3)
Thay (2), (3) vào (1), ta được: –b + 2b + 6 = 4.
Suy ra b = –2.
Với b = –2, thay vào (2) ta được 4a = 2.
Suy ra a = (thỏa mãn a > 0).
Vì vậy ta có , b = –2, c = 6.
Khi đó P = abc =
Vậy ta chọn phương án A.
Câu 3. Đồ thị hàm số y = mx2 – 2mx – m2 – 2 (m ≠ 0) là parabol có đỉnh nằm trên đường thẳng y = x – 3 thì m nhận giá trị nằm trong khoảng nào dưới đây?
A. (1; 6);
B. (–∞;–2);
C. (–3; 3);
D. (0; +∞).
Hướng dẫn giải
Đáp án: C
Giải thích:
Hàm số đã cho có dạng y = ax2 + bx + c, với a = m, b = –2m, c = –m2 – 2 (m ≠ 0).
Suy ra b’ = –m.
∆ = b’2 – ac = (–m)2 – m.(–m2 – 2) = m3 + m2 + 2m.
Đỉnh S có tọa độ:
⦁
⦁
Do đó yS = –m2 – m – 2 (vì m ≠ 0).
Suy ra tọa độ đỉnh S(1; –m2 – m – 2).
Vì đỉnh S nằm trên đường thẳng y = x – 3 nên ta có:
–m2 – m – 2 = 1 – 3.
Suy ra –m2 – m = 0
Khi đó m = 0 (loại) hoặc m = –1 (thỏa mãn).
Vì vậy m ∈ (–3; 3).
Vậy ta chọn phương án C.
Câu 4. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học phát hiện ra rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ có cân nặng P(n) = 360 – 10n. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất?
A. 3 240;
B. 40;
C. 20;
D. 18.
Hướng dẫn giải
Đáp án: D
Giải thích:
Gọi T là trọng lượng tất cả số con cá trên một đơn vị diện tích của mặt hồ.
Vì trên một diện tích của mặt hồ có n con cá nên ta có:
T = (360 – 10n).n = –10n2 + 360n.
Hàm số T có dạng T = an2 + bn + c, với a = –10, b = 360, c = 0.
∆ = b2 – 4ac = 3602 – 4.(–10).0 = 129 600.
Vì a = –10 < 0 nên hàm số đạt giá trị lớn nhất bằng tại
Khi đó khi
Vậy phải thả 18 con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất.
Câu 5. Một chiếc cổng hình parabol có phương trình . Biết cổng có chiều rộng d = 5 m. Chiều cao h của cổng bằng:
A. 4,45 m;
B. 3,125 m;
C. 4,125 m;
D. 3,25 m.
Hướng dẫn giải
Đáp án: B
Giải thích:
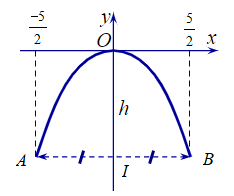
Gọi A và B là hai điểm ứng với chân cổng như hình vẽ.
Vì cổng hình parabol có phương trình và có chiều rộng d = 5 (m) nên ta có: AB = 5.
Gọi I là trung điểm AB. Suy ra IA = IB = (m).
Hàm số đã cho có dạng y = ax2 + bx + c, với , b = c = 0.
Vì b = 0 nên Oy là trục đối xứng của parabol.
Do đó trung điểm I của đoạn thẳng AB nằm trên Oy.
Khi đó điểm I có hoành độ bằng 0.
Vì IA = IB = nên ta có
Với , ta có
Suy ra tọa độ
Với , ta có
Suy ra tọa độ
Vì vậy chiều cao h của cổng là:
h = OI = |yA| = |yB| = (m).
Vậy ta chọn phương án B.
Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Bài 1: Hàm số và đồ thị
Trắc nghiệm Bài 2: Hàm số bậc hai
Trắc nghiệm Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°