Tailieumoi.vn xin giới thiệu chuyên đề Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số thuộc chương trình Toán 12. Chuyên đề gồm 182 trang với đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 12.

Chuyên đề Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Phần 1: Các dạng bài tập về sự đồng biến, nghịch biến của hàm số

A. LÝ THUYẾT.

1. Định nghĩa.

Cho hàm số y = f(x) xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn.

- Hàm số y = f(x) đồng biến (tăng) trên K nếu ∀ x₁, x₂∈ K, x₁ < x₂⇒ f(x₁) < f(x₂).

- Hàm số y = f(x) nghịch biến (giảm) trên K nếu ∀ x₁, x₂∈ K, x₁ < x₂⇒ f(x₁) > f(x₂).

2. Điều kiện cần để hàm số đơn điệu.

Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.

– Nếu hàm số đồng biến trên khoảng K thì f'(x) ≥ 0, ∀ x ∈ K 

– Nếu hàm số nghịch biến trên khoảng K thì f'(x) ≤ 0, ∀ x ∈ K.

3. Điều kiện đủ để hàm số đơn điệu.

Giả sử hàm số y = f(x) có đạo hàm trên khoảng K.

– Nếu f'(x) > 0, ∀x ∈ K thì hàm số đồng biến trên khoảng K.

– Nếu f'(x) < 0, ∀x ∈ K thì hàm số nghịch biến trên khoảng K.

– Nếu f'(x) = 0, ∀x ∈ K thì hàm số không đổi trên khoảng K.

Lưu ý

– Nếu f'(x) ≥ 0, ∀x ∈ K (hoặc f'(x) ≤ 0, ∀x ∈ K) và f'(x) = 0 chỉ tại một số điểm hữu hạn của K thì hàm số đồng biến trên khoảng K (hoặc nghịch biến trên khoảng K).

B. CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Phần I. Các bài toán không chứa tham số.

Dạng 1: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.

1. Phương pháp giải.

Bước 1. Tìm tập xác định D.

Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị x_i (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.

Bước 4. Sắp xếp các giá trị x_i theo thứ tự tăng dần và lập bảng biến thiên.

Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất.

2. Ví dụ minh hoạ.

Ví dụ 1. Cho hàm số y = x³ + 3x² – 9x – 7  . Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên khoảng (-3;1) .

B. Hàm số đồng biến trên (-9;-5).

C. Hàm số đồng biến trên R.     

D. Hàm số đồng biến trên (5;+∞).

Lời giải

Tập xác định: D = R. 

Ta có: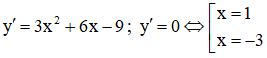 

Bảng biến thiên:

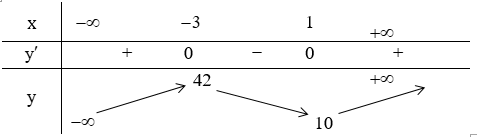
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)

Chọn C.

Ví dụ 2. Các khoảng nghịch biến của hàm số y = -x⁴ + 2x² - 4 là

A. (-1;0) và (1;+∞)                                  B. (-∞;1) và (1;+∞) 

C. (-1;0) và (0;1)                                     D. (-∞;1) và (0;1) 

Lời giải

Tập xác định: D = R. 

Ta có: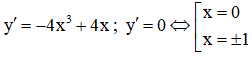 

Bảng biến thiên

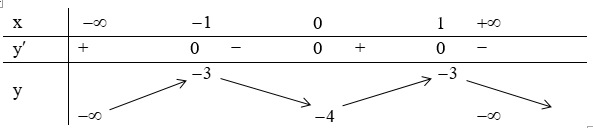
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;1), (0;1) . Hàm số nghịch biến trên các khoảng: (-1;0), (1;+∞) 

Chọn A.

Ví dụ 3. Chọn mệnh đề đúng về hàm số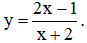 

A. Hàm số nghịch biến trên từng khoảng xác định của nó.

B. Hàm số đồng biến trên tập xác định của nó.

C. Hàm số đồng biến trên từng khoảng xác định của nó.

D. Hàm số nghịch biến trên tập xác định của nó.

Lời giải

Tập xác định: D = R\{-2} .Ta có: 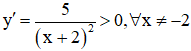. Nên hàm số đồng biến trên từng khoảng xác định của nó.

Bảng biến thiên

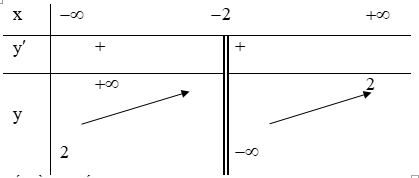
Kết luận: hàm số đồng biến trên từng khoảng xác định.

Chọn C.

Ví dụ  4. Cho hàm số 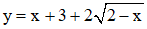. Khẳng định nào sau đây là khẳng đúng

A. Hàm số đồng biến trên khoảng (-∞;-2) và nghịch biến trên khoảng (-2;2) 

B. Hàm số đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1;2) 

C. Hàm số nghịch biến trên khoảng (-∞;-2) và đồng biến trên khoảng (-2;2) 

D. Hàm số nghịch biến trên khoảng (-∞;1) và đồng biến trên khoảng (1;2)

Lời giải

Tập xác định: D = (-∞;2] .

Đạo hàm: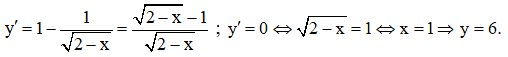 

Bảng biến thiên:

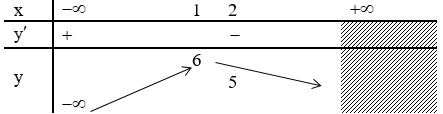
Kết luận: hàm số đã cho đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1;2)

Chọn B.

Ví dụ 5. Cho hàm số 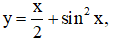 với x ∈ [0;π] . Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên [0;π]              B. Hàm số nghịch biến trên [0;π]

C. Hàm số nghịch biến trên 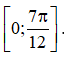D. Hàm số nghịch biến trên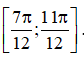 

Lời giải

Tập xác định: D = [0;π] 

Đạo hàm: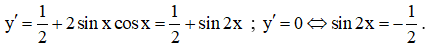 

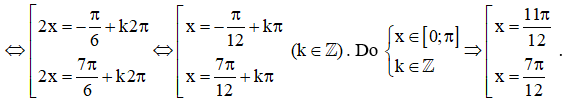
Bảng biến thiên

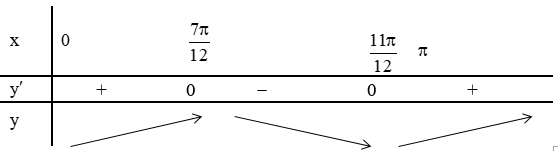
Chọn D.

3. Bài tập tự luyện.

Câu 1. Cho hàm số y = -x³ + 3x² - 3x + 2. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên R.

B. Hàm số nghịch biến trên các khoảng (-∞;1) và (1;+∞).

C. Hàm số đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1;+∞).

D. Hàm số luôn đồng biến trên R.

Câu 2. Hỏi hàm số nào sau đây luôn nghịch biến trên R?

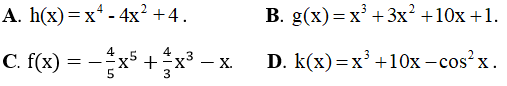
Câu 3. Hỏi hàm số 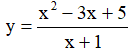 nghịch biến trên các khoảng nào ?

A. (-∞;-4) và (2;+∞).           B. (-4;2) .

C. (-∞;-1) và (-1;+∞)          D. (-4;-1) và (-1;2).

Câu 4. Hỏi hàm số 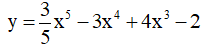 đồng biến trên khoảng nào?

A. (-∞;0).               B. R.              C. (0;2).              D. (2;+∞).

Câu 5. Cho hàm số y = ax³ + bx² + cx + d. Hỏi hàm số luôn đồng biến trên R khi nào?

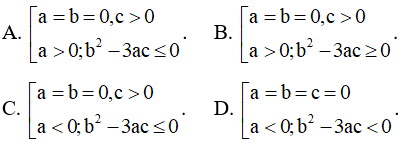
Câu 6. Cho hàm số 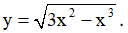 Khẳng định nào sau đây là khẳng định sai?

A. Hàm số đồng biến trên khoảng (0;2).

B. Hàm số đồng biến trên các khoảng (-∞;0); (2;3)

C. Hàm số nghịch biến trên các khoảng (-∞;0); (2;3)

D. Hàm số nghịch biến trên khoảng (2;3)

Câu 7. Cho các hàm số sau: 

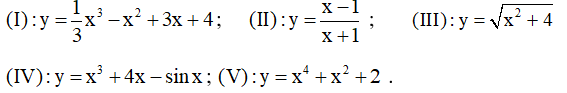
Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định?

A. 2.            B. 4.            C. 3.            D. 5.

Câu 8. Cho các hàm số sau:

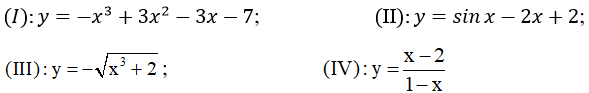
Hỏi hàm số nào nghịch biến trên toàn trục số?

A. (I), (II).                       B. (I), (II) và (III).  

C. (I), (II) và (IV).           D. (II), (III).

Câu 9. Xét các mệnh đề sau:

 (I). Hàm số y = -(x - 3)³ nghịch biến trên R.

(II). Hàm số 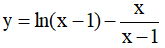 đồng biến trên tập xác định của nó.

(III). Hàm số 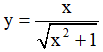 đồng biến trên R.

Hỏi có bao nhiêu mệnh đề đúng?

A. 3.            B. 2.            C. 1.            D. 0.

Câu 10. Cho hàm số 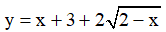. Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số nghịch biến trên khoảng (-∞;-2) và đồng biến trên khoảng (-2;2)

B. Hàm số đồng biến trên khoảng (-∞;-2) và nghịch biến trên khoảng (-2;2).

C. Hàm số đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1;2)

D. Hàm số nghịch biến trên khoảng (-∞;1) và đồng biến trên khoảng (1;2)

Câu 11. Hàm số 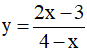. Chọn phát biểu đúng:

A. Luôn đồng biến trên R.        

B. Luôn nghịch biến trên từng khoảng xác định.

C. Đồng biến trên từng khoảng xác định.

D. Luôn nghịch biến trên R.

Câu 12. Cho hàm số y = -x³ + 3x² + 2021. Khoảng đồng biến của hàm số này là

A. (0;+∞).             B. (-∞;0).               C. (2;+∞).                 D. (0; 2).

Câu 13. Cho hàm số: f(x) = -2x³ + 3x² + 12x -1. Trong các mệnh đề sau, tìm mệnh đề sai:

A. f(x) nghịch biến trên khoảng (5;10).        B. f(x) giảm trên khoảng (-1; 3)

C. f(x) nghịch biến trên khoảng (-3; -1)       D. f(x) đồng biến trên khoảng (-1; 1)

Câu 14. (ĐỀ THI THPT QUỐC GIA NĂM 2017). Hàm số nào đồng biến trên khoảng (-∞;+∞)

A. y = -x³ - 3x .      B. y = x³ + x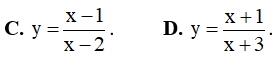 

Câu 15. Tập xác định của hàm số 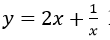 là:

A. D = R\{-1}               B. D = R.               C. R\.               D. R\

Câu 16. Khẳng định nào sau đây sai?

A. Hàm số y = 2x + cosx luôn đồng biến trên R.

B. Hàm số y = -x³ - 3x + 1 luôn nghịch biến trên R

C. Hàm số 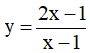 luôn đồng biến trên mỗi khoảng xác định.

D. Hàm số y = 2x⁴ + x² + 1 luôn nghịch biến trên (-∞;0).

Câu 17. Cho hàm số 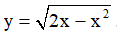. Hàm số nghịch biến trên khoảng nào dưới đây?

A. (0;2).                B. (0;1).                    C. (1;2).                D. (-1;1).

Câu 18. Hàm số nào sau đây đồng biến trên  ?

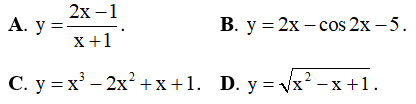
Câu 19. Cho y = 2x⁴ - 4x². Hãy chọn mệnh đề sai trong bốn phát biểu sau:

A. Hàm số nghịch biến trên các khoảng ( -∞; -1) và (0;1).

B. Hàm số đồng biến trên các khoảng (-∞;-1) và (1;+ ∞).

C. Trên các khoảng (-∞;-1) và (0;1), y’ < 0 nên hàm số nghịch biến.

D. Trên các khoảng (-1;0) và (1;+ ∞), y’ > 0 nên hàm số đồng biến.

Câu 20. (ĐỀ THPT QG 2017)  Hàm số nào sau đây đồng biến trên R.

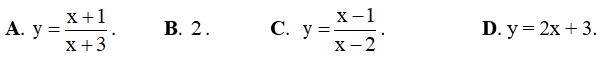
Đáp án

 

Dạng 2: Từ bảng biến thiên, đồ thị hàm số của hàm số f’(x), xác định khoảng đồng biến, nghịch biến của hàm số đã cho.

1. Phương pháp giải.

- Dựa vào bảng biến thiên có sẵn, kết luận khoảng đồng biến, nghịch biến và chọn đáp án đúng.

- Từ đồ thị hàm số của hàm số f’(x), ta có:

+ Khoảng đồng biến của hàm số là khoảng mà tại đó giá trị f'(x) > 0 (nằm phía trên trục hoành).

+ Khoảng đồng biến của hàm số là khoảng mà tại đó f'(x) < 0 (nằm phía dưới trục hoành).

Xét bài toán: Cho bảng biến thiên của hàm số f’(x). Xét tính đồng biến, nghịch biến của hàm số g(x) theo f(x).

- Các bước giải:

Bước 1: Ta tính đạo hàm g^'(x) 

Bước 2: Kết hợp các nguyên tắc xét dấu tích, thương, tổng (hiệu) và bảng biến thiên của f’(x) để có được bảng xét dấu cho g^'(x)

Bước 3: Dựa vào bảng xét dấu của g^'(x) vừa có để kết luận về sự đồng biến, nghịch biến của hàm số g(x).

2. Ví dụ minh hoạ.

Ví dụ. Cho hàm số y = f(x) có bảng biến thiên như hình bên. Hàm số y = -2018.f(x) đồng biến trên khoảng nào dưới đây?

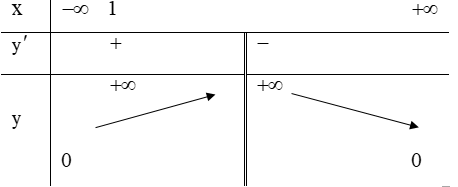
A. (-∞;0)               B. (1;+ ∞)               C. (0;+ ∞)             D. (-∞;1)

Lời giải

Đặt g(x) = -2018.f(x), ta có: g^'(x) = -2018.f^'(x).

Xét g^'(x) = -2018.f^'(x) ≥ 0 ⇔ f^'(x) ≤ 0 ⇔ x ≥ 1

Vậy hàm số y = -2018.f(x) đồng biến trên khoảng (1;+ ∞) 

Chọn B.

3. Bài tập tự luyện.

Câu 1. Cho hàm số y = f(x) có đạo hàm liên tục trên [-3,3] và hàm số y = f^'(x) có đồ thị như hình vẽ bên dưới.

 

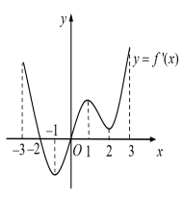
Hàm số y = f(x) nghịch biến trên khoảng nào?

A. (2;3).               B. (0;2)               C. (-1;0).             D. (-3;-1)

Câu 2. Cho hàm số f(x) có bảng biến thiên như sau:

 

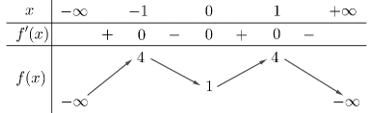
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. (1;+ ∞)                   B. (-1;1) .               C. (0;1)                  D. (-1;0) .

Câu 3. Cho hàm số y = f(x). Biết f(x) có đạo hàm là f^'(x) và hàm số y = f^'(x) có đồ thị như hình vẽ bên. 

 

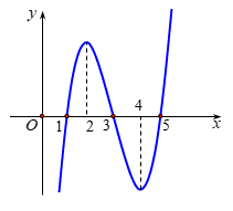
Kết luận nào sau đây là đúng?

A. Hàm số y = f(x) chỉ có hai điểm cực trị.

B. Hàm số y = f(x) đồng biến trên khoảng (1;3). 

C. Hàm số y = f(x) đồng biến trên khoảng (-∞;2)

D. Hàm số y = f(x) nghịch biến trên khoảng (4;+ ∞)

Câu 4. Cho hàm số f(x) xác định trên R và có đồ thị của hàm số f^'(x) như hình vẽ.

 

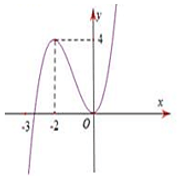
 Mệnh đề nào sau đây đúng?

A. Hàm số y = f(x) đồng biến trên khoảng (-∞;2); (0;+ ∞).

B. Hàm số y = f(x) nghịch biến trên khoảng (-2;0)  

C. Hàm số y = f(x) đồng biến trên khoảng (-3;+ ∞) 

D. Hàm số y = f(x) nghịch biến trên khoảng (-∞;0).

Câu 5. Cho hàm số f(x) xác định trên R và có đồ thị của hàm số f^'(x) như hình vẽ. 

 

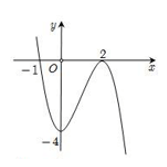
Mệnh đề nào sau đây đúng?

A. Hàm số y = f(x) đồng biến trên khoảng (-4,2) 

B. Hàm số y = f(x) đồng biến trên khoảng (-∞;-1)  

C. Hàm số y = f(x) đồng biến trên khoảng (0,2) 

D. Hàm số y = f(x) nghịch biến trên khoảng (-∞;-4) và (2;+ ∞) 

Câu 6. Cho hàm số f(x) có đạo hàm f^'(x) xác định, liên tục trên R và f^'(x) có đồ thị như hình vẽ bên. 

 

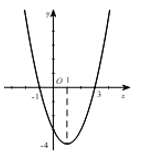
Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên (1;+ ∞)

B. Hàm số đồng biến trên (-∞;-1)  và (3;+ ∞) 

C. Hàm số nghịch biến trên (-∞;-1)  

D. Hàm số đồng biến trên (-∞;-1) ∪ (3;+ ∞)

Câu 7.  Cho hàm số f(x) có đạo hàm f^'(x) xác định, liên tục trên R và f^'(x) có đồ thị như hình vẽ bên. 

 

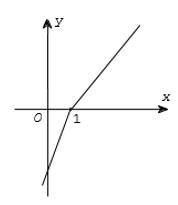
Khẳng định nào sau đây là đúng?

A. Hàm số f(x) đồng biến trên (-∞;1)  

B. Hàm số f(x) đồng biến trên (-∞;1) và (1;+ ∞) 

C. Hàm số f(x) đồng biến trên (1;+ ∞) 

D. Hàm số f(x) đồng biến trên R 

Câu 8. Cho hàm số f(x) = ax⁴ + bx³ + cx² + dx + e (a ≠ 0). Biết rằng hàm số f(x) có đạo hàm là f^'(x) và hàm số y = f^'(x) có đồ thị như hình vẽ bên. 

 

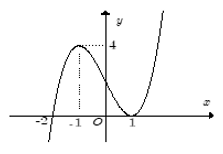
Khi đó nhận xét nào sau đây là sai?

A. Trên (-2,1) thì hàm số f(x) luôn tăng.

B. Hàm f(x) giảm trên đoạn [-1,1]

C. Hàm f(x) đồng biến trên khoảng (1;+ ∞)

D. Hàm f(x) nghịch biến trên khoảng (-∞;-2)

Câu 9. Cho hàm số y = f(x) liên tục và xác định trên R. Biết f(x) có đạo hàm f^'(x) và hàm số y = f^'(x) có đồ thị như hình vẽ:

 

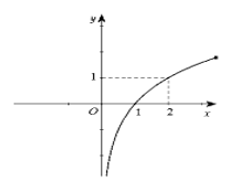
Khẳng định nào sau đây đúng?

A. Hàm số f(x) đồng biến trên R 

B. Hàm số f(x) nghịch biến trên R  

C. Hàm số f(x) chỉ nghịch biến trên khoảng (0,1) 

D. Hàm số f(x) đồng biến trên khoảng (0;+ ∞)

Câu 10. Cho hàm số y = f(x) có bảng biến thiên như sau

 

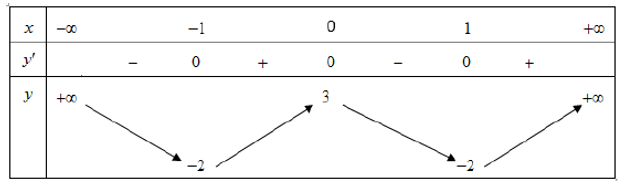
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (-1;0)                B. (-∞;0)

C. (1;+∞)              D. (0;1)

Đáp án

1	2	3	4	5	6	7	8	9	10
D	C	B	C	B	B	C	B	C	D

 

Dạng 3. Xét sự đồng biến, nghịch biến của hàm hợp.

1. Phương pháp giải.

Bài toán 1: Cho hàm y = f(x) hoặc hàm y = f^'(x) xét sự biến thiên của hàm g(x) = f(u(x)).

Phương pháp: 

- Tính đạo hàm g^'(x) = f^'(u(x)).u^'(x)

- Xét dấu g^'(x) dựa vào dấu của f^'(u(x)) và u^'(x) theo quy tắc nhân dấu.  Lưu ý khi xét dấu f^'(u(x)) dựa vào dấu của f^'(x) như sau: Nếu f^'(x) không đổi dấu trên D thì f^'(u(x)) không đổi dấu khi u(x) ∈ D.

Bài toán 2: Cho hàm y = f(x) hoặc y = f^'(x) xét sự biến thiên của hàm g(x) = f(u(x)) + h(x)

Phương pháp: 

- Tính g^'(x) = f^'(u(x)).u^'(x) + h^'(x) 

- Lập bảng xét dấu g^'(x) bằng cách cộng dấu của hai biểu thức f^'(u(x)).u^'(x) và h^'(x) 

Bài toán 3: Cho hàm y = f(u(x)) hoặc hàm y = f^'(u(x)) xét sự biến thiên của hàm y = f(x)

Phương pháp: Giả sử ta có: f^'(u(x)) > 0 ⇔x ∈ D. Ta cần giải BPT f^'(x) > 0

- Đặt t = u(x) => x = v(t) 

- Giải bất phương trình: f^'(t) > 0 ⇔ f^'(u(x)) > 0 ⇔x ∈ D ⇔ x = v(t) ∈ D ⇔ t ∈ D^'

- Vậy  f^'(t) > 0 ⇔ x ∈ D^' 

2. Ví dụ minh hoạ.

Ví dụ 1. Cho hàm số f(x) , bảng xét dấu của f^'(x) như sau:

 

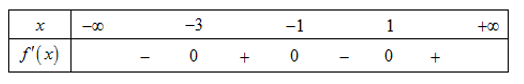
Hàm số f(5 - 2x) nghịch biến trên khoảng nào dưới đây?

A. (2;3).                         B. (0;2).                     

C. (3;5).                         D. (5;+∞).

Lời giải

Ta có y = f(5 - 2x) → y^' = -2f^'(5 - 2x)  

Hàm số nghịch biến khi y^' = -2f^'(5 - 2x) ≤ 0 ⇔ f^'(5 - 2x) ≥ 0

Dựa vào bảng xét dấu ta thấy khi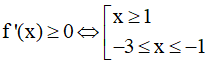  

Nên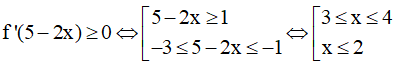   

Vậy hàm số y = f(5 - 2x) nghịch biến trên các khoảng (3,4) và (-∞;2)

Chọn B

Ví dụ 2. Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị hàm f^'(x) như hình vẽ dưới đây. Hàm số g(x) = f(x² - x) đồng biến trên khoảng nào?

 

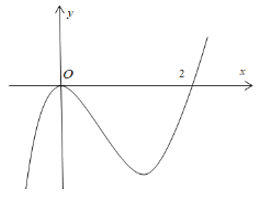
Lời giải

Ta có: g(x) = f(x² - x) => g^'(x) = (2x - 1)f^'(x² - x)

 

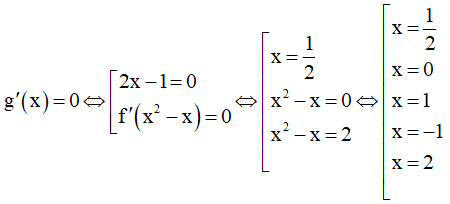
Từ đồ thị f^'(x) ta suy ra f^'(x) > 0 ⇔ x > 2   

Do đó :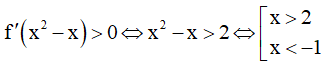  

 (Ta cần xác định một loại dấu của )

Bảng xét dấu g^'(x): 

 

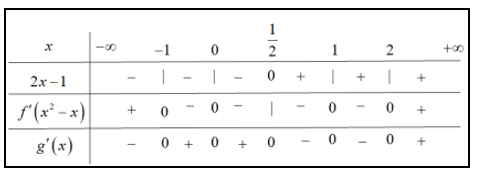
Từ bảng xét dấu ta có hàm số g(x) đồng biến trên khoảng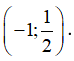 

Chọn C.

Lưu ý: Dấu của g^'(x) ở bảng trên có được nhờ nhân dấu của hai biểu thức (2x - 1) và f^'(x² - x) 

Ví dụ 3. Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:

 

Hàm số y = 3f(x + 2) - x³ + 3x đồng biến trên khoảng nào dưới đây?

A. (5;+∞)                            B. (-∞;-1)       

C. (-1,0)                             D. (0,2)

Lời giải

Ta có y^' = 3f^'(x + 2) - 3x² + 3 = 3[f^'(x + 2) + (1 - x²)] 

Xét f^'(x + 2) = 0 ⇔ x + 2 ∈ ⇔ x ∈ {-1,0,1,2}

Xét 1 - x² = 0 ⇔ x = 1, x = -1

Lại có: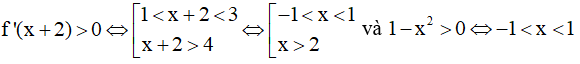 

Bảng xét dấu 

 

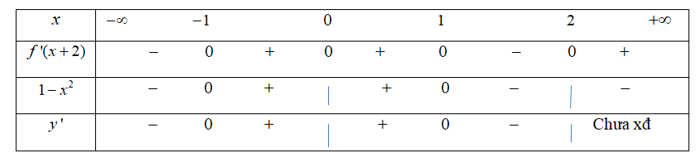
Từ bảng xét dấu suy ra trên khoảng (-1,0) hàm số đồng biến. 

Chọn C.

Ví dụ 4. Cho hàm số y = f(x) có đạo hàm trên R. Hàm số y = f^'(3x - 1)  có đồ thị như hình vẽ:

 

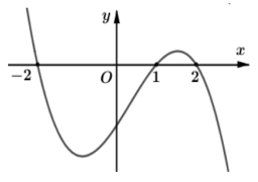
Hàm số đồng biến trên khoảng nào dưới đây?

A. (2,6)                             B. (-∞;-7)       

C. (-∞;-6)                         D.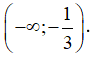 

Lời giải

Ta cần giải BPT dạng f^'(x) > 0.

Ta có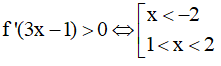  

Đặt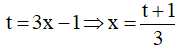  

Do đó: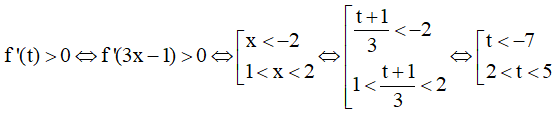  

Vậy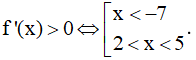 

Chọn B.

Ví dụ 5.  Cho hàm số y = f(x) có 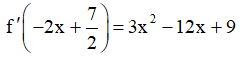. Hàm số y = f(x) nghịch biến trên khoảng nào sau đây.

Lời giải

Ta cần giải bất phương trình f^'(x) < 0 .

Từ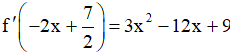 

Đặt 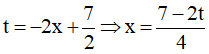. Khi đó ta có  .

Vậy hàm số y = f(x) nghịch biến trên khoảng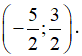 

Chọn C.

                                 

3. Bài tập tự luyện.

Bài 1.  Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f^'(3x + 5) như hình vẽ. Hàm số y = f(x) nghịch trên khoảng nào?

 

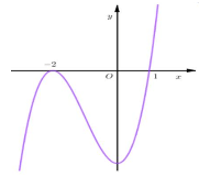
Bài 2. Cho hàm số y = f(x) có đồ thị hàm số y = f^'(2 - x) như hình vẽ bên. Hỏi hàm số y = f(x) đồng biến trên khoảng nào sau đây?

 

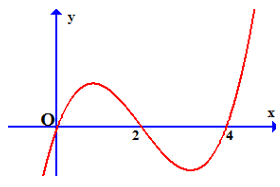
A. (-2,4) .                 B. (-1,3)                 C. (-2,0)             D. (0,1)

Bài 3. Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y = f^'(x) như hình vẽ bên dưới.

 

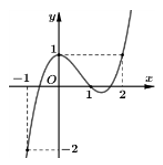
Hàm số 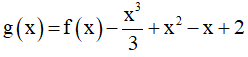 đồng biến trên khoảng nào trong các khoảng sau?

A. (-1,0)                       B. (0,2)                  C. (1,2)                   D. (0,1)

Bài 4. (Đề tham khảo BGD năm 2017-2018) Cho hàm số y = f(x). Hàm số y = f^'(x) có đồ thị như hình bên. Hàm số y = f(2 - x) đồng biến trên khoảng:

 

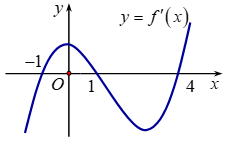
A. (1;3)                                B. (2;+∞)        

C. (-2;1)                               D. (-∞;2)

Bài 5. (Sở GD&ĐT Nam Định năm 2018-2019) Cho hàm số f(x) liên tục trên R và có đạo hàm f’(x) thỏa mãn f’(x) = (1-x)(x+2)g(x) + 2018 với g(x) < 0,∀x ∈ R. Hàm số y = f(1-x) + 2018x + 2019 nghịch biến trên khoảng nào?

A. (1;+∞)                              B. (0;3)                   

C. (-∞;3)                               D. (4;+∞)

Bài 6.  Cho hàm số f’(x) có bảng xét dấu như sau:

 

Hàm số y = f(x² + 2x) nghịch biến trên khoảng nào dưới đây?

A. (-2;1)                            B. (-4;-3)        

C. (0;1)                             D. (-2;-1)

Bài 7. Cho hàm số f(x). Biết hàm số f’(x) có đồ thị như hình vẽ bên. Hàm số y = f(3 - x²) + 2018 đồng biến trong khoảng nào dưới đây?

 

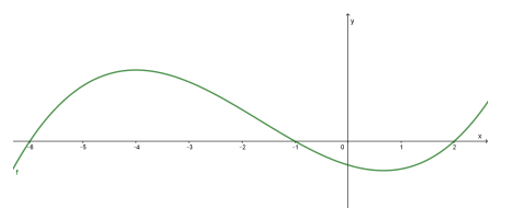
A. (-1;0).                              B. (2;3)                

C. (-2,-1) .                           D. (0;1)

Bài 8. Cho hàm số f(x) liên tục trên R, hàm số y = f^'(x) có đồ thị như hình vẽ. Xét hàm số h(x) = 2f(3x + 1) - 9x² - 6x + 4. Hãy chọn khẳng định đúng:

 

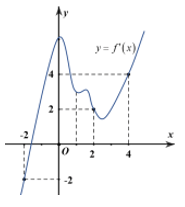
A. Hàm số h(x) nghịch biến trên R.           B. Hàm số h(x) nghịch biến trên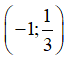  

C. Hàm số h(x) đồng biến trên 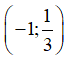D. Hàm số h(x) đồng biến trên R.

Bài 9. (Chuyên Quốc Học Huế năm 2018-2019) Cho hàm số f(x) có đạo hàm trên R là f’(x) = (x-1)(x+3). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;20] để hàm số y = f(x²+3x-m) đồng biến trên khoảng (0;2)?

A. 18                       B. 17                      C. 16                      D. 20

Bài 10. Cho hàm số f(x) có đồ thị của hàm số y = f^'(x - 2) + 2 như hình vẽ. 

 

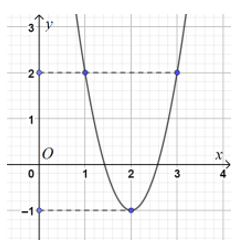
Hỏi hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?

A. (-1;1)                                B. (-∞;2)           

C. 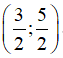                            D. (2;+∞)

Đáp án

 

Phần II. Các bài toán có chứa tham số.

Dạng 4. Tìm tham số m để hàm số đồng biến (nghịch biến) tập xác định (khoảng xác định) của hàm số.

1. Phương pháp giải.

Bài toán 1. Tìm tham số m để hàm số y = ax³ + bx² + cx + d đơn điệu trên R

Bước 1: Tập xác định: D = R

Bước 2: Đạo hàm y^' = 3ax² + 2bx + c .

Bước 3: Điều kiện đơn điệu (khi a ≠ 0).

- Hàm số đồng biến trên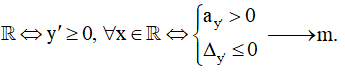  

- Hàm số nghịch biến trên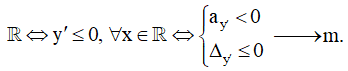  

Lưu ý: Nếu hàm bậc ba y = ax³ + bx² + cx + d có a chứa tham số thì ta cần xét a = 0 để kiểm tra xem hàm số có đơn điệu trên R hay không.

- Không xét bài toán tìm m để hàm số y = ax⁴ + bx² + c đơn điệu trên R do phương trình y’=0 luôn có ít nhất 1 nghiệm là x = 0.

Bài toán 2. Tìm tham số m để hàm số 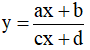 (c ≠ 0,ad - bc ≠ 0 ) đơn điệu trên mỗi khoảng xác định của nó. 

Phương pháp:

Bước 1: Tập xác định: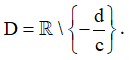 

Bước 2: Đạo hàm: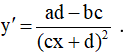

Bước 3: Điều kiện đơn điệu:

- Hàm số đồng biến trên mỗi khoảng xác định ⇔ y^' > 0,∀x ∈ D ⇔ ad - bc > 0 → m

- Hàm số nghịch biến trên mỗi khoảng xác định ⇔ y^' < 0,∀x ∈ D ⇔ ad - bc < 0 → m

Lưu ý: Nếu hàm số 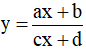 có c chứa tham số thì ta nên xét c = 0 để kiểm tra xem hàm số có đơn điệu trên từng khoảng xác định của nó hay không.

Mở rộng: 

* Tìm tham số  để hàm số 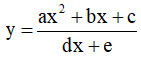 (ad ≠ 0 ) đơn điệu trên mỗi khoảng xác định của nó. 

Phương pháp:

Bước 1: Tập xác định: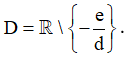 

Bước 2: Đạo hàm: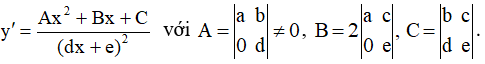 

Bước 3: Điều kiện đơn điệu:

- Hàm số đồng biến trên mỗi khoảng xác định ⇔ y^' ≥ 0,∀x ∈ D .

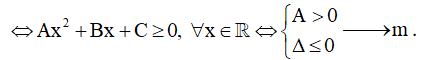
- Hàm số nghịch biến trên mỗi khoảng xác định ⇔ y^' < 0,∀x ∈ D

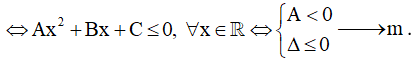
Lưu ý: Nếu gặp câu hỏi tương tự dành cho hàm số 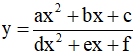 thì ta cũng làm theo phương pháp nêu trên.

- Đối với bài toán 2, đạo hàm y^' chỉ lớn hơn 0 hoặc nhỏ hơn 0 chứ không được cho y^' ≥ 0,y^' ≤ 0. Lý do là nếu ta cho y^' = 0 thì sẽ có vô số giá trị x thỏa mãn (mà định nghĩa nêu rõ y^' = 0 tại một số hữu hạn điểm x mà thôi).

* Tìm tham số m để hàm số lượng giác đơn điệu trên R 

Cách 1.

- Tính đạo hàm y^' = f^'(x), cho y^' = f^'(x) ≥ 0 nếu đề bài yêu cầu hàm số đồng biến trên R (Ngược lại: y^' = f^'(x) ≤ 0 nếu đề bài yêu cầu hàm số nghịch biến trên R )

- Cô lập m để có được dạng g(m) ≥ h(x)  

(hoặc g(m) ≤ h(x);g(m) > h(x);g(m) < h(x) ).

- Tìm Max-Min cho hàm số h(x) trên R (Hoặc lập bảng biến thiên cho hàm h(x)).

- Dựa vào giá trị Max-Min hoặc bảng biến thiên để kết luận về điều kiện của m.

Cách 2. Đặt t = sinx (hoặc t = cosx ) với điều kiện t ∈ [-1,1] 

Bất phương trình: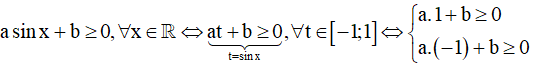  

Hoàn toàn tương tự: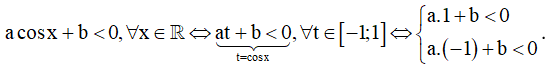 

2. Ví dụ minh hoạ.

Ví dụ 1. Cho hàm số y = -x³ - mx² + (4m + 9)x + 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (-∞;+∞)  

A. 4                      B. 6                         C. 7                               D. 5 

Lời giải

TXĐ: D = R . 

Đạo hàm y^' = -3x² - 2mx + 4m + 9 

Để hàm số đã cho nghịch biến trên khoảng (-∞;+∞) ⇔ y^' ≤ 0,∀x ∈ R     

( y^' = 0 có hữu hạn nghiệm). 

Do a = -3 < 0 nên y’ ≤ 0 ⇔ Δ^' ≤ 0 ⇔ m² + 3(4m + 9) ≤ 0 ⇔ -9 ≤ m ≤ -3. 

 

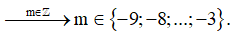
Vậy có 7 giá trị m thoả mãn điều kiện bài toán.

Chọn C.

Sai lầm hay gặp là ^''Để hàm số đã cho nghịch biến trên khoảng (-∞;+∞) thì ⇔ y^' < 0,∀x ∈ R^''. Khi đó ra giải ra -9 ≤ m ≤ -3 và chọn D.

Ví dụ 2. Hàm số 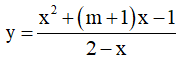 ( m là tham số) nghịch biến trên mỗi khoảng xác định của nó khi các giá trị của m là:

A. m ≥ 1 .               B. m = 1 .             C. 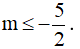D. -1 < m < 1

Lời giải

Tập xác định: D = R\. 

Đạo hàm: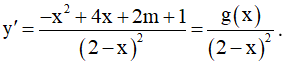 

Hàm số nghịch biến trên mỗi khoảng xác định của nó khi và chỉ khi y^' ≤ 0,∀x ∈ R 

(Dấu ^'' = ^'' chỉ xảy ra tại hữu hạn điểm trên D )

⇔ g(x) = -x² + 4x + 2m + 1 ≤ 0, ∀x ∈ D . 

Do a = -1 < 0, nên g(x) ≤ 0 . 

⇔ Δ_g^' ≤ 0 ⇔ 4 - (-1).(2m + 1) ≤ 0 ⇔ 2m + 5 ≤ 0 ⇔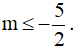 

Chọn C.

3. Bài tập tự luyện.

Câu 1. Hàm số y = x³ + mx đồng biến trên R khi:

A. Chỉ khi m = 0.            B. Chỉ khi m ≥ 0.

C. Chỉ khi m ≤ 0.            D. Với mọi m.

Câu 2. Tìm m lớn nhất để hàm số 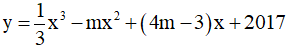 đồng biến trên R ?

A. m = 1.               B. m = 2.               C. Đáp án khác.              D. m = 3.

Câu 3. Hàm số 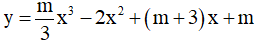 luôn đống biến trên R thì giá trị m nhỏ nhất là:

A. m = - 4.             B. m = 0.               C. m = - 2.                       D. m = 1.

Câu 4. Hàm số 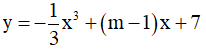 nghịch biến trên R thì điều kiện của m là:

A. m > 1.               B. m = 2.               C. m ≤ 1.                         D. m ≥ 2.

Câu 5. Hàm số 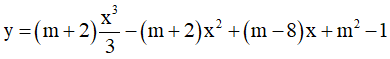 nghịch biến trên R thì:

A. m < - 2.             B. m > - 2.            C. m ≤ -2.             D. m ≥ - 2.

Câu 6. Cho hàm số y = x³ - (m + 1)x² - (2m² - 3m + 2)x + 2m(2m - 1). Khẳng định nào sau đây là đúng?

A. Hàm số luôn nghịch biến.     

B. Hàm số luôn đồng biến.

C. Hàm số không đơn điệu trên R .               

D. Các khẳng định A, B, C đều sai.

Câu 7. Tìm điều kiện của a, b để hàm số y = 2x + a sinx + bcosx luôn luôn đồng biến trên R .

A. a² + b² ≤ 2 .       B. a² + b² ≥ 2         C. a² + b² ≤ 4          D. a² + b² ≥ 2

Câu 8. Giá trị của b để hàm số f(x) = sinx - bx + c nghịch biến trên toàn trục số là:

A. b ≥ 1.           B. b < 1 .          C. b = 1 .        D. b ≤ 1 .

Câu 9. Nếu hàm số   nghịch biến thì giá trị của m là:

A. (-∞;2) .         B. (2;+∞) .        C. R\ .        D. (-1;2) .

Câu 10. Tìm tất cả các giá trị thực của tham số α và β sao cho hàm số 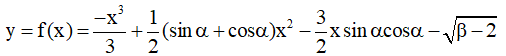 luôn giảm trên R ?

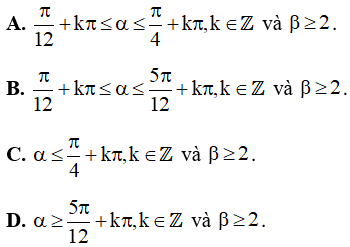
Câu 11. Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y = f(x) = 2x + asinx + bcosx luôn tăng trên R ?

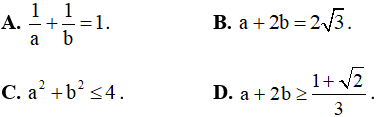
Câu 12. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 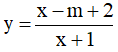 giảm trên các khoảng mà nó xác định ?

A. m < -3                    B. m ≤ -3                     C. m ≤ 1                  D. m < 1

Câu 13. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên R ?

 

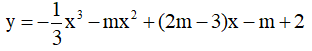
A. -3 ≤ m ≤ 1                B . m ≤ 1                C. -3 < m < 1         D. m ≤ -3; m ≥ 1

Câu 14. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 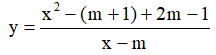 tăng trên từng khoảng xác định của nó?

A. m > 1 .                     B. m ≤ 1                   C. m < 1               D. m ≥ 1

Câu 15. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f(x) = x + m cosx luôn đồng biến trên R ?

Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn đồng biến trên R ?

y = 2x3 - 3(m + 2)x² + 6(m + 1)x - 3m + 5 

A. 0.                  B. –1.                    C. 2.                     D. 1.

Câu 17. Tìm số nguyên m nhỏ nhất sao cho hàm số 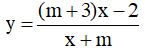 luôn nghịch biến trên các khoảng xác định của nó?

A. m = -1.               B. m = -2               C. m = 0             D. Không có  

Câu 18. Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số 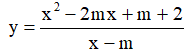 đồng biến trên từng khoảng xác định của nó?

A. 2.               B. 4.                  C. Vô số.               D. Không có.

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
B	D	D	C	C	C	C	A	D	B	C	D	A	B	A	A	D	C

 

Dạng 5. Tìm m để hàm số đồng biến (nghịch biến) trên một khoảng xác định K cho trước.

Bài toán 1. Tìm tham số m để hàm số bậc ba, bậc bốn,… đơn điệu trên tập K cho trước (với K là khoảng, đoạn hoặc nửa khoảng).

Phương pháp:

Bước 1: Tìm đạo hàm của hàm y^' = f^'(x) .

Bước 2: Điều kiện đơn điệu:

- Hàm số đồng biến trên K ⇔ y^' ≥ 0,∀x ∈ K .

- Hàm số nghịch biến trên K ⇔ y^' ≤ 0,∀x ∈ K.

Bước 3: 

*Tìm tham số m để hàm số y = ax³ + bx² + cx + d đơn điệu trên một khoảng có độ dài p.

Phương pháp:

Bước 1: Đạo hàm y^' = 3ax² + 2bx + c.

Bước 2: 

- Hàm số đồng biến trên khoảng có độ dài p ⇔ y^' có hai nghiệm phân biệt x₁,x₂ thỏa mãn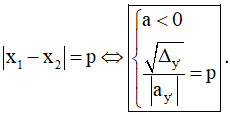 

- Hàm số nghịch biến trên khoảng có độ dài p ⇔ y^' có hai nghiệm phân biệt x₁,x₂ thỏa mãn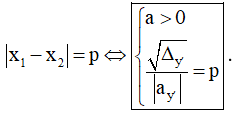 

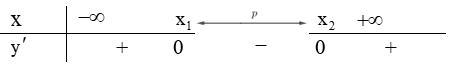
Lưu ý: 

- Dạng này không cần điều kiện a ≠ 0,Δ > 0 vì điều kiện 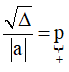 đã bao hàm hai ý trên.

-  Điều kiện |x₁ - x₂| = p có thể được xử lý theo hai cách chính: 

+ Một là sử dụng định lí Vi-ét: |x₁ - x₂| = p ⇔ x₁² - 2x₁x₂ + x₂² = p²

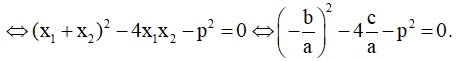
+ Hai là tự xây dựng công thức: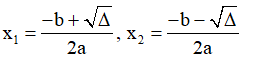 

  

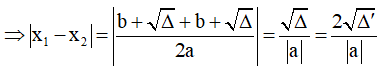
Các câu hỏi: “đồng biến (nghịch biến) trên khoảng có độ dài > p, ≥ p; < p; ≤ p” ta cũng sẽ làm tương tự.

Bài toán 2: Tìm tham số m để hàm số nhất biến 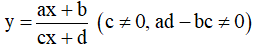 đơn điệu trên một khoảng K cho trước (với K là khoảng, đoạn hoặc nửa khoảng).

Phương pháp:

Bước 1: Tập xác định: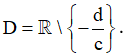 

Bước 2: Đạo hàm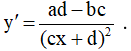 

Bước 3: Điều kiện đơn điệu:

- Hàm số đồng biến trên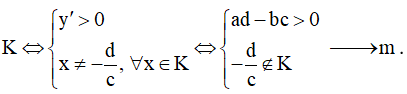 

- Hàm số nghịch biến trên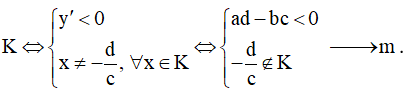 

* Tìm tham số m để hàm số 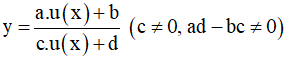 đơn điệu trên khoảng K cho trước.

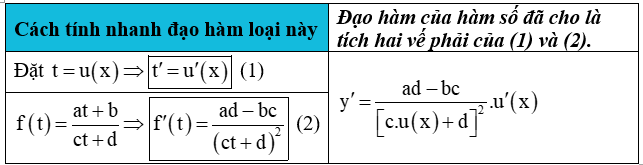
Bài toán 3. Bài toán tham số đối với những dạng hàm số khác.

Phương pháp:

Bước 1: Tìm đạo hàm của hàm y^' = f^'(x).

Bước 2: Điều kiện đơn điệu:

- Hàm số đồng biến trên K ⇔ y^' ≥ 0,∀x ∈ K.

- Hàm số nghịch biến trên K ⇔ y^' ≤ 0,∀x ∈ K

Bước 3: 

- Biến đổi theo dạng m ≥ g(x) ∀x ∈ K (hoặc m ≤ g(x) ∀x ∈ K ).

- Lập bảng biến thiên của hàm số g(x) với mọi ∀x ∈ K

Dựa vào bảng biến thiên và kết luận điều kiện cho tham số  

- Giả sử hàm g(x) tồn tại Max-Min trên R. Ta có:

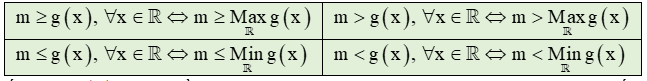
- Nếu hàm g(x) không tồn tại Max-Min trên R, tuy nhiên thông qua bảng biến thiên ta tìm được điều kiện bị chặn: M₁ < g(x) < M₂, khi đó:

2. Ví dụ minh hoạ.

Ví dụ 1. (Đề tốt nghiệp THPT 2020 mã đề 103) Tập hợp tất cả các giá trị thực của tham số m để hàm số 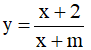 đồng biến trên khoảng (-∞,-5)  

A. (2,5] .              B. [2,5)           C. (2;+∞) .        D. (2,5)

Lời giải

Chọn A

Tập xác định: D = R\{-m} 
Ta có: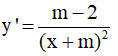  

Hàm số đồng biến trên khoảng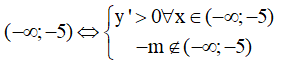 

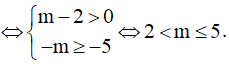
Ví dụ 2. (Đề Minh họa lần 1, 2017, BGD) Tìm tất cả các giá trị của m để hàm số 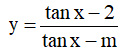 đồng biến trên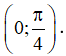 

A. m < 2 .                     B.  m ≤ 0 hoặc 1 ≤ m < 2

C. 1 ≤ m < 2 .               D. m ≤ 0 .

Lời giải

Điều kiện: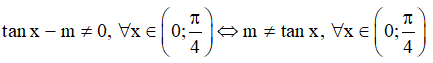 

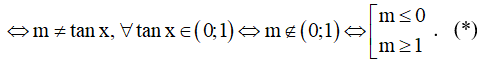
Tính đạo hàm nhanh bằng phương pháp sau:

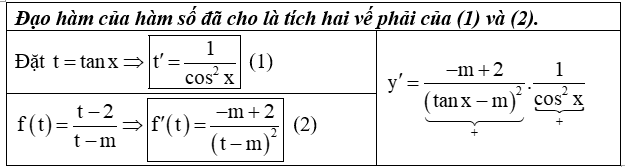
Ta có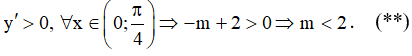 

Từ (*) và (**) suy ra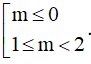 

Chọn B.

Ví dụ 3. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x³ - 3x² + (2 - m)x đồng biến trên khoảng (2;+∞) là:

A. (-∞,-1]                  B. (-∞,2)                C. (-∞,-1)                 D. (-∞,2]

Lời giải

Ta có y^' = 3x² - 6x + 2 - m . 

Để hàm số đồng biến trên khoảng (2;+∞) khi và chỉ khi y^' ≥ 0, ∀x ∈ (2;+∞)   

⇔ 3x² - 6x + 2 - m ≥ 0, ∀x ∈ (2;+∞) ⇔ m ≤ 3x² - 6x + 2, ∀x ∈ (2;+∞)  

Xét hàm số f(x) = 3x² - 6x + 2, ∀x ∈ (2;+∞) 

f^'(x) = 6x - 6; f^'(x) = 0 => 6x - 6 = 0 ⇔ x = 1;  .

Bảng biến thiên:

 

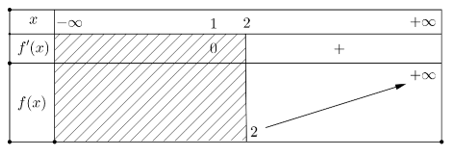
Từ bảng biến thiên ta thấy m ≤ 2. Vậy m ∈ (-∞,2] .

Chọn D.

Ví dụ 4. Tìm tất cả giá trị thực của m để hàm số y = x³ + (m + 1)x² + 4x + 7 có độ dài khoảng nghịch biến đúng bằng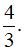 

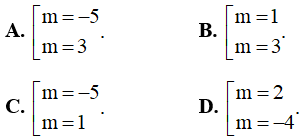
Lời giải

Đạo hàm y^' = 3x² + 2(m + 1)x + 4  .

Hàm số có độ dài khoảng nghịch biến đúng bằng 2√5 ⇔ y^' = 0 có hai nghiệm phân biệt thỏa mãn :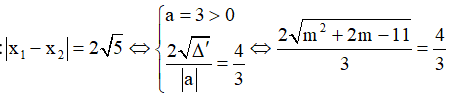 

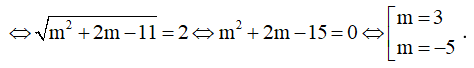
Chọn A.

3. Bài tập tự luyện.

Câu 1. (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101) Tập hợp tất cả các giá trị thực của tham số m để hàm số 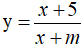 đồng biến trên khoảng (-∞;-7) là

A. [4;7) .               B. (4;7]              C. (4;7)               D. (4;+∞) .

Câu 2. (Đề tốt nghiệp THPT 2020 mã đê 102) Tập hợp tất cả các giá trị thực của tham số m để hàm số 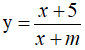 đồng biến trên khoảng (-∞;-8) là

A. (5;+∞).                B. (5;8].                C. [5;8).                D. (5;8).

Câu 3. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 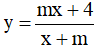 giảm trên khoảng m(-∞;1) ?

A. -2 < m < 2 .      B. -2 ≤ m ≤ -1.     C. -2 < m ≤ -1 .     D. -2 ≤ m ≤ 2.

Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 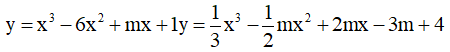 đồng biến trên khoảng (0;+∞) ?

A. m ≤ 0.              B. m ≤ 12.             C. m ≥ 0.              D. m ≥ 12

Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 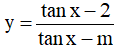 đồng biến trên khoảng  ?

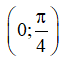A. 1 ≤ m < 2.              B. m ≤ 0; 1 ≤ m < 2             C. m ≥ 2              D. m ≤ 0

Câu 6. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 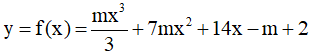 giảm trên nửa khoảng [1,+∞) ?

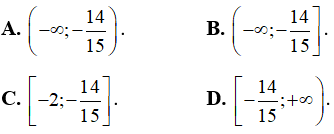
Câu 7. Tất cả các giá trị thực của tham số m sao cho hàm số y = -x⁴ + (2m - 3)x² + m nghịch biến trên khoảng (1,2) là 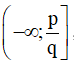 , trong đó phân số  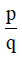tối giản và q >0. Hỏi tổng q + p là?

A. 5.                     B. 9.                     C. 7.                     D. 3.

Câu 8. Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số 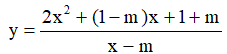 đồng biến trên khoảng (1,+∞)  ?

A. 3.                     B. 1.                     C. 2.                     D. 0.

Câu 9. Hàm số y = x³ - (m + 1)x² - (2m² - 3m + 2)x + 2m(2m - 1) đồng biến trên miền  [2;+∞) khi:

Câu 10. Tập tất cả các giá trị của m để hàm số 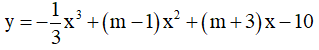 đồng biến trên khoảng (0;3) là:

A. m = 0.               B. 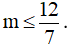. C. 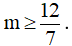D. m tùy ý.

Câu 11. Biết rằng hàm số 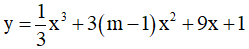 nghịch biến trên (x₁, x₂) và đồng biến trên các khoảng còn lại của tập xác định. Nếu |x₁ - x₂| = 6√3 thì giá trị m là:

A. -1.                      B. 3.                      C. - 3 hoặc 1.         D. - 1 hoặc 3. 

Câu 12. Giá trị của m để hàm số y = x³ + 3x² + mx + m giảm trên đoạn có độ dài bằng 1 là:

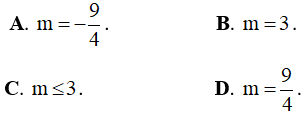
Câu 13. Hàm số y = x⁴ - 2(m - 1)x² + m - 2 đồng biến trên (1;3) khi:

A. m ∈ [-5;2) .                         B. m ∈ (-∞;2]   

C. m ∈ (-∞;-5)                         D. m ∈ (2;+∞)

Câu 14. Hàm số 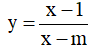 nghịch biến trên khoảng (-∞;2) khi và chỉ khi:

A. m > 2.               B. m ≥ 1.               C. m ≥ 2.               D. m > 1.

Câu 15. Hàm số 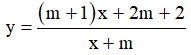 nghịch biến trên (-1; +∞)  khi:

A. m < 1.               B. m > 2.               C. 1≤ m < 2.                 D.- 1 < m < 2.

Câu 16. Tìm tất cả giá trị thực của tham số m sao cho hàm số 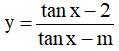 đồng biến trên khoảng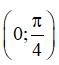  

A. m ≤ 0 hoặc 1 ≤ m < 2 .             B. m ≤ 0 .            C. 1 ≤ m < 2 .           D. m ≥ 2

Câu 17. Tìm các giá trị của tham số m để hàm số 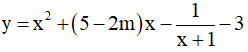 đồng biến trên (-1; +∞)

A. ∀m ∈ R .                    B. m ≤ 6                    C. m ≥ -3                D. m ≤ 3

Câu 18. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số sau đồng biến trên R : 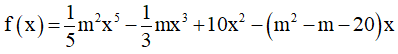. Tổng giá trị của tất cả các phần tử thuộc S bằng

Đáp án

Phần III. Bài toán ứng dụng sự đồng biến, nghịch biến của hàm số.

1. Phương pháp giải.

Bài toán 1: Đánh giá các bất đẳng thức f(x) ≥ 0, ∀x ∈ [a;b] hoặc f(x) ≥ g(x), ∀x ∈ [a;b].

Phương pháp

Chuyển vế để đưa bất đẳng thức về dạng f(x) ≥ 0, ∀x ∈ [a;b] 

Bước 1: Tính đạo hàm f^'(x) và chứng minh đạo hàm chỉ mang một dấu (âm hoặc dương).

Bước 2: Vận dụng tính chất đơn điệu:

- Nếu hàm f(x) đồng biến trên [a;b] thì ∀x ∈ [a;b], 0 ≤ f(a) ≤ f(x) ≤ f(b) 

- Ngược lại nếu hàm f(x) nghịch biến trên [a;b] thì f(a) ≥ f(x) ≥ f(b) ≥ 0

Bài toán 2: Giải phương trình dạng f(u) = f(v) với u,v ∈ D .

Phương pháp:

Bước 1: Nhận diện hàm đặc trưng để đưa phương trình về dạng f(u) = f(v) với u,v ∈ D, ∀x ∈ [a;b]. 

Bước 2: Chứng minh hàm đặc trưng f(t) đơn điệu trên D( f^'(t) luôn âm hoặc luôn dương trên D ).

Bước 3: Giải phương trình: f(u) = f(v) ⇔ u = v

Bài toán 3: Giải phương trình dạng f(x) = g(x) có nghiệm duy nhất x = x₀ 

Phương pháp:

Bước 1: Tìm một nghiệm x = x₀ của phương trình (bằng tính nhẩm hoặc nhân lượng liên hợp v.v…).

Bước 2: Tính đạo hàm f^'(x) và chứng minh đạo hàm chỉ mang một dấu (tức là hàm f(x) đơn điệu trên miền xác định). 

Bước 3: Chứng minh hàm số g(x) là hàm hằng hoặc đơn điệu (ngược lại hàm f(x) ). Từ đó khẳng định phương trình đã cho có nghiệm duy nhất  x = x₀ 

2. Ví dụ minh hoạ.

Ví dụ 1. Cho hàm y = f(x) số có f^'(x) < 0,∀x ∈ R. Tìm tất cả các giá trị thực của x để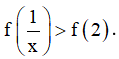 

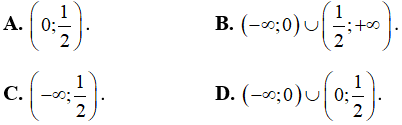
Lời giải

Ta có: f^'(x) < 0, ∀x ∈ R nên hàm số y = f(x) nghịch biến trên R

Do đó: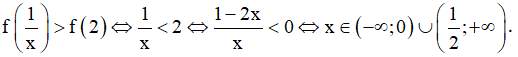 

Chọn D.

Ví dụ 2. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Cho hàm số f(x) có bảng biến thiên như sau:

 

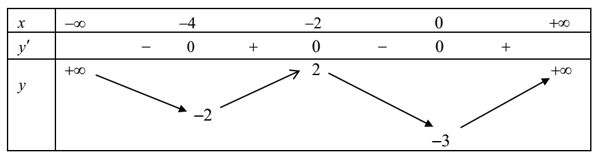
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x² - 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0, +∞) ?

A. 15 .                   B. 12 .                    C. 14 .                   D. 13.

Lời giải

Đặt u = x² - 4x  (1)

Ta có BBT sau:

 

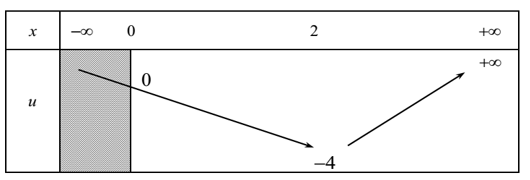
Ta thấy:

+ Với u < -4, phương trình (1) vô nghiệm.

+ Với u = -4, phương trình (1) có một nghiệm x = 2 > 0 .

+ Với -4 < u < 0, phương trình (1) có hai nghiệm x > 0 .

+ Vơi u ≥ 0, phương trình (1) có một nghiệm x > 0 

Khi đó 3f(x² - 4x) = m => 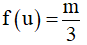(2), ta thấy:

+ Nếu 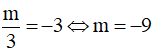, phương trình (2) có một nghiệm u = 0 nên phương trình đã cho có một nghiệm x > 0 .

+ Nếu 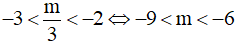, phương trình (2) có một nghiệm u > 0 và một nghiệm u ∈ (-2,0) nên phương trình đã cho có ba nghiệm x > 0 .

+ Nếu 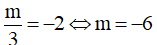, phương trình (2) có một nghiệm u = -4, một nghiệm u ∈ (-2,0) và một nghiệm u > 0 nên phương trình đã cho có bốn nghiệm x > 0

+ Nếu 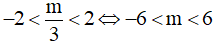, phương trình (2) có một nghiệm u < -4, hai nghiệm u ∈ (-4,0) và một nghiệm u > 0 nên phương trình đã cho có năm nghiệm x > 0

+ Nếu 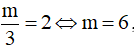, phương trình (2) có một nghiệm u < -4, một nghiệm u = -2 và một nghiệm u > 0 nên phương trình đã cho có ba nghiệm x > 0

+ Nếu  , phương trình (2) có một nghiệm u < -4 và một nghiệm u > 0 nên phương trình đã cho có một nghiệm x > 0

Vậy -9 < m ≤ 6 => có 15 giá trị  m nguyên thỏa yêu cầu bài toán.

Chọn A.

Ví dụ 3. Khi giải phương trình: 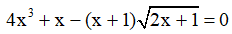, ta tìm được nghiệm có dạng  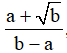với a, b là các số nguyên. Hãy tính a² + b².

A. a² + b² = 13             B. a² + b² = 9             C. a² + b² = 41           D. a² + b² = 26 

Lời giải

Điều kiện: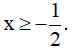 

Phương trình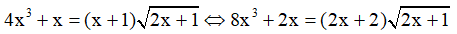  

 (*)

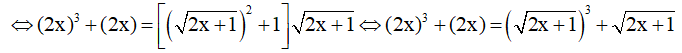Chọn f(t) = t³ + t với t ≥ 0. Ta có f^'(t) = 3t + 1 > 0, ∀t ≥ 0 . Vậy hàm số f(t) đồng biến trên [0,+∞) .

Phương trình (*) được viết: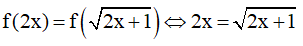  

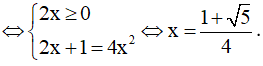
Với định dạng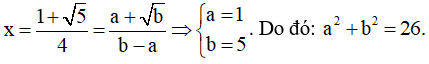 

Chọn D.

3. Bài tập tự luyện.

Câu 1. Tìm tất cả các giá trị thực của tham số m sao cho phương trình x³ - 3x² - 9x - m = 0 có đúng 1 nghiệm?

A. -27 ≤ m ≤ 5.                          B. m < -5 hoặc m > 27.

C. m < -27 hoặc m > 5 .            D. -5 ≤ m ≤ 27

Câu 2. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 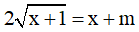 có nghiệm thực?

A. m ≥ 2.              B. m ≤ 2.              C. m ≥ 3 .               D. m ≤ 3.

Câu 3. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 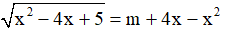 có đúng 2 nghiệm dương?

A. 1 ≤ m ≤ 3.         B. -3 < m < √5.    C. -√5 < m < 3.    D. -3 ≤ m < 3

Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x² - 3x + 2 ≤ 0 cũng là nghiệm của bất phương trình mx² + (m + 1)x + m + 1 ≥ 0 ?

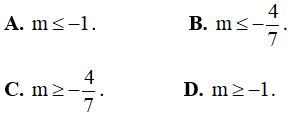
Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho phương trình: 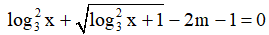 có ít nhất một nghiệm trên đoạn [1; 3^√3]  ?

A. -1 ≤ m ≤ 3.           B. 0 ≤ m ≤ 2          C. 0 ≤ m ≤ 3          D. -1 ≤ m ≤ 2

Câu 6. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 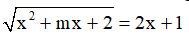 có hai nghiệm thực?

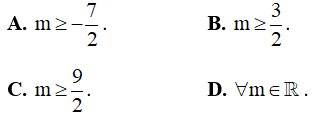
Câu 7. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 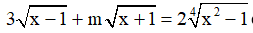 có hai nghiệm thực?

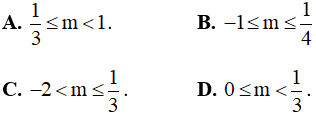
Câu 8. Tìm tất cả các giá trị thực của tham số sao cho bất phương trình 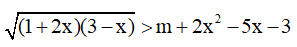 nghiệm đúng với mọi  ?

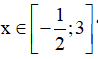A. m > 1 .               B. m > 0 .              C. m < 1 .               D. m < 0 .

Câu 9. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 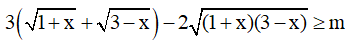 nghiệm đúng với mọi x ∈ [-1;3] ?

A. m ≤ 6 .                B. m ≥ 6 .                C. m ≥ 6√2 - 4.               D. m ≤ 6√2 - 4 

Câu 10. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 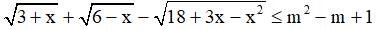 nghiệm đúng ∀x ∈ [-3,6]?

A. m ≥ -1 .                        B. -1 ≤ m ≤ 0.

C. 0 ≤ m ≤ 2 .                   D. m ≤ -1 hoặc m ≥ 2 .

 

Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình m.4^x + (m - 1).2^x+2 + m - 1 > 0 nghiệm đúng ∀x ∈ R?

A. m ≤ 3              B. m ≥ 0               C. -1 ≤ m ≤ 4                 D. m ≥ 0

Câu 12. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: 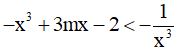 nghiệm đúng ∀x ≥ 1 ?

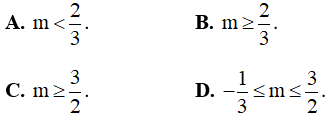
Câu 13. Tìm giá trị lớn nhất của tham số m sao cho bất phương trình 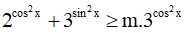 có nghiệm?

A. m =4 .              B. m =8.              C. m =12             D. m =16.

Câu 14. Bất phương trình 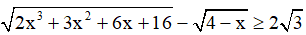 có tập nghiệm là [a,b]. Hỏi tổng a + b có giá trị là bao nhiêu? 

A. 2 .                   B. 4.                     C. 5.                     D. 3.

Câu 15. Bất phương trình 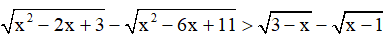 có tập nghiệm (a,b]. Hỏi hiệu b - a có giá trị là bao nhiêu?

A. 1.                     B. 2.                     C. 3.                     D. -1 .

 

Đáp án

Phần 2: Các dạng bài tập về cực trị của hàm số

A. LÝ THUYẾT

1. Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a,b) và điểm x₀ ∈ (a,b).

- Nếu tồn tại số h > 0 sao cho f(x) < f(x₀)  với mọi x ∈ (x₀ - h; x₀ + h) và x ≠ x₀ thì ta nói hàm số f(x) đạt cực đại tại x₀.

- Nếu tồn tại số h > 0 sao cho f(x) > f(x₀) với mọi x ∈ (x₀ - h; x₀ + h) và x ≠ x₀ thì ta nói hàm số f(x) đạt cực tiểu tại x₀ .

2. Điều kiện cần để hàm số có cực trị.

Định lý 1: Giả sử hàm số f(x) đạt cực trị tại điểm x_o. Khi đó, nếu f(x) có đạo hàm tại điểm x_o thì f‘(x_o) = 0.

Lưu ý: 

- Đạo hàm f‘(x) có thể bằng 0 tại điểm x_o nhưng hàm số f(x) không đạt cực trị tại điểm x_o.

- Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.

- Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0, hoặc tại đó hàm số không có đạo hàm.

- Hàm số đạt cực trị tại x_o và nếu đồ thị hàm số có tiếp tuyến tại điểm (x_o ; f(x_o)) thì tiếp tuyến đó song song với trục hoành.

Ví dụ : Hàm số y = |x| và hàm số y = x³

3. Điều kiện đủ để hàm số có cực trị.

Định lý 2: Giả sử hàm số y = f(x) liên tục trên K = (x₀ - h; x₀ + h) và có đạo hàm trên K hoặc trên K\, với h > 0 .

- Nếu f‘(x) > 0 trên khoảng (x₀ - h; x₀) và f‘(x) < 0 trên (x₀ ; x₀ + h) thì x₀ là một điểm cực đại của hàm số f(x) .

- Nếu f‘(x) < 0 trên khoảng (x₀ - h; x₀) và f‘(x) > 0  trên (x₀ ; x₀ + h) thì x₀ là một điểm cực tiểu của hàm số f(x) .

Minh họa bằng bảng biến thiến

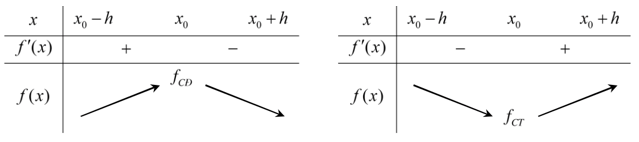
Lưu ý: 

- Như vậy: Điểm cực trị phải là một điểm trong của tập hợp D (D ⊂ℝ). Nếu f’(x) không đổi dấu thì hàm số không có cực trị.

(Nhấn mạnh:x_o ∈ (a; b) ⊂ D nghĩa là x_o là một điểm nằm ở giữa trong của D).

Ví dụ: Hàm số y = √x xác định trên D= [0,+∞). Ta có y ≥ y (0) với mọi x, nhưng x = 0 không phải là cực tiểu của hàm số vì D không chứa bất kì 1 lân cận nào của điểm 0. 

^- Nếu hàm số y = f (x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f (x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là f_CĐ ( f_CT ), còn điểm M (x₀;f( x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

^- Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

- Giá trị cực đại (cực tiểu) f(x_o) nói chung không phải là GTLN (GTNN) của  f(x) trên tập hợp D.

- Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp D. Hàm số cũng có thể không có điểm cực trị.

- x_o là một điểm cực trị của hàm số f(x) thì điểm (x_o ; f(x_o)) được gọi là điểm cực trị của đồ thị hàm số f(x) .

4. Định lý 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng (a; b) chứa điểm x_o ;  f ‘(x_o) = 0 và f có đạo hàm cấp hai khác 0 tại điểm x_o

a) Nếu f ”(x_o) < 0 thì hàm số f  đạt cực đại tại điểm x_o
b) Nếu f ”(x_o) < 0 thì hàm số f  đạt cực tiểu tại điểm x_o

Lưu ý:

- Không cần xét hàm số f(x) có hay không có đạo hàm tại điểm x = x_o nhưng không thể bỏ qua điều kiện hàm số liên tục tại điểm x_o.

B. CÁC KỸ NĂNG GIẢI TOÁN CƠ BẢN.

1. Quy tắc tìm cực trị của hàm số.

Quy tắc 1. 

Bước 1:  Tìm tập xác định của hàm số.

Bước 2: Tính f^'(x). Tìm các điểm tại đó f^'(x) bằng 0 hoặc  f^'(x) không xác định.

Bước 3: Lập bảng biến thiên.

Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2.

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính  f^'(x). Giải phương trình  f^'(x) và ký hiệu x_i (i = 1,2,3...) là các nghiệm.

Bước 3: Tính  f^''(x) và  f^''(x_i) .

Bước 4: Dựa vào dấu của f^''(x_i) suy ra tính chất cực trị của điểm x_i .

2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba y = ax³ + bx² + cx + d ( a ≠ 0).

- Ta có y^' = 3ax² + 2bx + c 

Đồ thị hàm số có 2 điểm cực trị khi phương trình y^' = 0 có hai nghiệm phân biệt ⇔ b² - 3ac > 0 .

Và không có cực trị ⇔Δ’ = b²  − 3ac ≤ 0

- Cho hàm số y = ax³ + bx² + cx + d có hai điểm cực trị phân biệt là A, B . Khi đó:

Phương trình đường thẳng AB :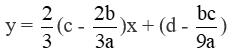 

Độ dài đoạn thẳng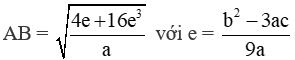 

Hoặc khi đó đường thẳng qua hai điểm cực trị liên quan tới: 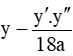(CASIO hỗ trợ).

3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C) .

Ta có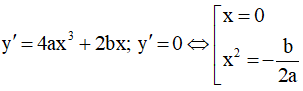  

(C) có ba điểm cực trị y^' = 0 có 3 nghiệm phân biệt 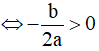 hay ab < 0

Hàm số có 3 cực trị là: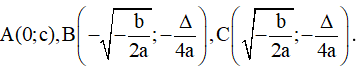 

Độ dài các đoạn thẳng: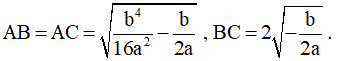 

C. CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Tìm các điểm cực trị của hàm số.

1. Phương pháp giải.

Quy tắc 1: Áp dụng định lý 2

- Tìm  f’(x)

- Tìm các điểm x_i (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm

- Xét dấu của  f’(x). Nếu  f’(x) đổi dấu khi x qua điểm x_o  thì hàm số có cực trị tại điểm x_o

Quy tắc 2: Áp dụng định lý 3

- Tìm  f’(x)

- Tìm các nghiệm x_i (i = 1, 2, 3,…) của phương trình f ‘(x) = 0 

- Với mỗi x_i tính f ”(x_i)

- Nếu f ”(x_i) < 0 thì hàm số đạt cực đại tại điểm x_i

- Nếu f ”(x_i) > 0 thì hàm số đạt cực tiểu tại điểm x_i

2. Ví dụ minh hoạ.

Ví dụ 1. (Đề thi THPTQG năm 2021) Cho hàm số y = f(x) có bảng biến thiên như sau:

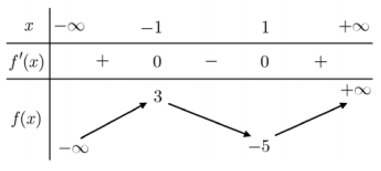
Giá trị cực đại của hàm số đã cho là

    A. 3                          B. -1.                     C. -5                             D. 1 .

Lời giải

Dựa vào bảng biến thiên, giá trị cực đại của hàm số là y = f(-1) = 3 .

Chọn A.

Ví dụ 2. (Đề tốt nghiệp 2020 - Đợt 2 Mã đề 103)  Cho hàm số f(x) có đạo hàm f^'(x) = x(x + 1)(x - 4)³, ∀x ∈ R. Số điểm cực đại của hàm số đã cho là:

A. 2 .                                     B. 3 .                      C. 4 .                      D. 1 .

Lời giải

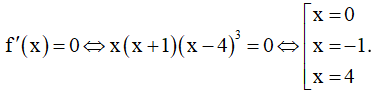
Lập bảng biến thiên của hàm số f(x) 

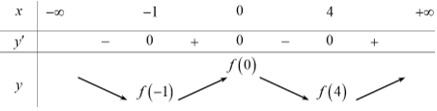
Vậy hàm số đã cho có một điểm cực đại.

Chọn D.

Ví dụ 3. (Đề tốt nghiệp 2020 - Đợt 1 Mã đề 101) Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:

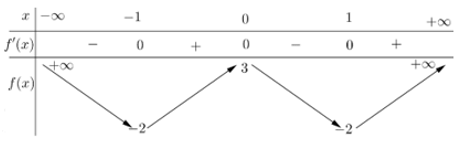
Số điểm cực trị của hàm số g(x) = x⁴[f(x + 1)]² là

A. 11 .                       B. 9 .                         C. 7 .                         D. 5 .

Lời giải

Ta chọn hàm f(x) = 5x⁴ - 10x² + 3 .

Đạo hàm 

g^'(x) = 4x³[f(x + 1)]² + 2x⁴f(x + 1)f^'(x + 1) = 2x³f(x + 1)[2f(x + 1) + xf^'(x + 1)]

Ta có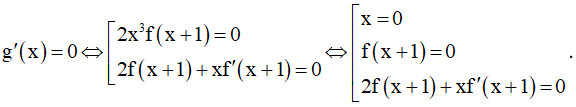 

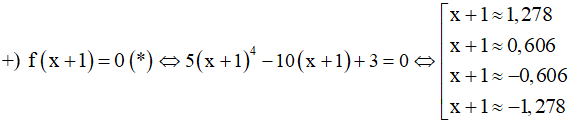
=> Phương trình có bốn nghiệm phân biệt khác 0. 

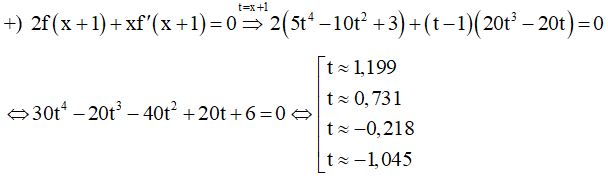
=> Phương trình có bốn nghiệm phân biệt khác 0 và khác các nghiệm của phương trình (∗) . 

Vậy số điểm cực trị của hàm số g(x) là 9.

Chọn B.

Ví dụ 4. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = -2x³ + 3x² + 1 .

A. y = x -1          B. y = x +1      C. y = -x +1       D. y = -x -1

Lời giải

Ta có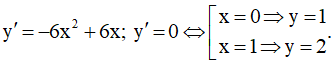 

Suy ra đồ thị hàm số đã hai điểm cực trị là A(0,1) và B(1,2).

Khi đó, đường thẳng đi qua hai điểm cực trị chính là đường thẳng AB có phương trình y = x +1 

Chọn B.

Cách 2. Lấy y chia cho y^', ta được ⇔  .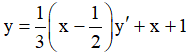

Suy ra phương trình đường thẳng đi qua hai điểm cực trị là phần dư trong phép chia, đó là y = x +1 

3. Bài tập tự luyện.

Câu 1. Cho hàm số f(x) xác định, liên tục và có đạo hàm trên khoảng (a,b). Mệnh đề nào sau đây là sai?

A. Nếu f(x) đồng biến trên (a,b) thì hàm số không có cực trị trên (a,b).

B. Nếu f(x) nghịch biến trên (a,b) thì hàm số không có cực trị trên (a,b).

C. Nếu f(x) đạt cực trị tại điểm x₀ ∈ (a,b) thì tiếp tuyến của đồ thị hàm số tại điểm M(x₀; f(x₀)) song song hoặc trùng với trục hoành.

D. Nếu f(x) đạt cực đại tại x₀ ∈ (a,b) thì f(x) đồng biến trên (a;x₀) và nghịch biến trên (x₀;b) .

Câu 2. Cho khoảng (a,b) chứa điểm x₀, hàm số f(x) có đạo hàm trên khoảng (a,b) (có thể trừ điểm x₀). Mệnh đề nào sau đây là đúng?

A. Nếu f(x) không có đạo hàm tại x₀ thì f(x) không đạt cực trị tại x₀

B. Nếu f^'(x) = 0 thì f(x) đạt cực trị tại điểm x₀

C. Nếu f^'(x₀) = 0 và f^''(x₀) = 0 thì f(x) không đạt cực trị tại điểm x₀

D. Nếu f^'(x₀) = 0 và f^''(x₀) ≠ 0 thì f(x) đạt cực trị tại điểm x₀

Câu 3. Phát biểu nào sau đây là đúng?

A. Nếu f^'(x) đổi dấu từ dương sang âm khi x qua điểm x₀ và f(x) liên tục tại x₀ thì hàm số y = f(x) đạt cực đại tại điểm x₀

B. Hàm số y = f(x) đạt cực trị tại x₀ khi và chỉ khi x₀ là nghiệm của f^'(x) = 0 

C. Nếu f^'(x₀) = 0 và f^''(x₀) = 0 thì x₀ không là điểm cực trị của hàm số y = f(x)

D. Nếu f^'(x₀) = 0 và f^''(x₀) > 0 thì hàm số đạt cực đại tại x₀

Câu 4. Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng (x₀ - h; x₀ + h) với h > 0 Khẳng định nào sau đây là sai?

A. Nếu f^'(x₀) = 0 và f^''(x₀) > 0 thì x₀ là điểm cực tiểu của hàm số.

B. Nếu f^'(x₀) = 0 và f^''(x₀) < 0 thì x₀ là điểm cực đại của hàm số.

C. Nếu f^'(x₀) = 0 và f^''(x₀) = 0 thì x₀ không là điểm cực trị của hàm số.

D. Nếu f^'(x₀) = 0 và f^''(x₀) = 0 thì chưa kết luận được x₀ có là điểm cực trị của hàm số.

Câu 5. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Cho hàm số f(x) có bảng biến thiên như sau :

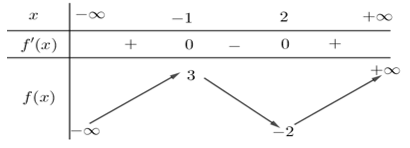
Điểm cực đại của hàm số đã cho là 

A. x = 3                   B. x = 2                     C. x = -2                     D. x = -1 

Câu 6. (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101) Cho hàm f(x) có bảng biến thiên như sau:

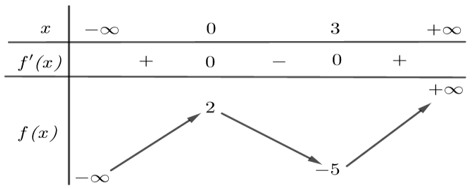
Giá trị cực tiểu của hàm số đã cho bằng 

A. 3                    B. -5                    C. 0                     D. 2

Câu 7. (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101) Cho hàm số f(x) liên tục trên R và có bảng xét dấu của f^'(x)  như sau:

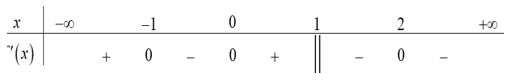
Số điểm cực đại của hàm số đã cho là

A. 4 .                         B. 1 .                        C. 2 .                        D. 3 .

Câu 8. Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là

A. 5 .                         B. 3 .                      C. 2 .                          D. 4 .

Câu 9. Cho hàm số có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng: 

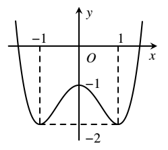
A. –1.                      B. –2.                       C. 1.                         D. 0.

Câu 10. Cho hàm số y = f(x) có đồ thị như hình vẽ. Đồ thị hàm số y = f(x) có mấy điểm cực trị?

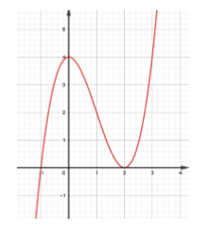
A. 0                          B. 2                            C. 1                            D. 3 

Câu 11. Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. 

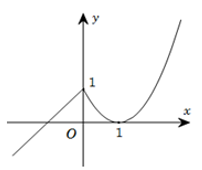
Hỏi hàm số có bao nhiêu điểm cực trị?

     A. 0.               B. 1.

     C. 3.               D. 2.

Câu 12. Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. 

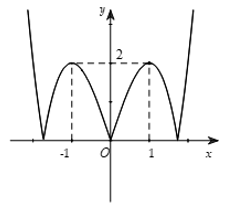
Hỏi hàm số có bao nhiêu điểm cực trị?

A. 2.               

B. 3.

C. 4.               

D. 5.

Câu 13. Hàm số y = 2x³ - x² + 5 có điểm cực đại là:

A. 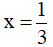                       B.  5                    C.  3                      D.  0

Câu 14. Tìm số điểm cực trị của đồ thị hàm số  ?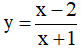

A. 4.                               B. 1.                           C. 0.                          D. 3.

Câu 15. Hàm số y = -x⁴ - x² + 1 có mấy điểm cực trị?

A. 3.                              B. 0.                           C. 1.                          D. 2.

Câu 16. Gọi x₁,x₂ là hai điểm cực trị của hàm số 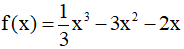. Giá trị của x₁² + x₂² bằng:

A. 13                             B. 32                          C. 4                           D. 36

Câu 17. Điểm cực tiểu của đồ thị hàm số y = 3x⁴ - 4x³ - 6x² + 12x + 1 là điểm M(x₀, y₀). Tính tổng T = x₀ + y₀ 

A. T = 8                        B. T = 4                   C. T = -11               D. T = 3 

Câu 18. Đồ thị hàm số nào sau đây có đúng 1 điểm cực trị?

A. y = -x⁴ - 3x² + 4              B. y = x³ - 6x² + 9x - 5

C. y = x³ - 3x² + 3x - 5        D. y = 2x⁴ - 4x² + 1

Câu 19. Đồ thị hàm số nào sau đây có 3 điểm cực trị?

A. y = 2x⁴ - 4x² + 1                 B. y = (x² + 1)² 

C. y = x³ - 6x² + 9x - 5            D. y = -x⁴ - 3x² + 4 

Câu 20. Cho hàm số y = f(x) liên tục trên R và có đạo hàm 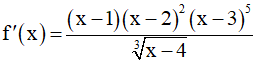. Hỏi hàm số y = f(x) có bao nhiêu điểm cực trị?

A. 2 .                                     B. 4 .                      C. 3 .                      D. 5 .

Câu 21. Gọi y₁,y₂ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số y = x³ - 3x² - 9x + 4. Tính P = y₁.y₂ 

A. P = -302 .         B. P = -82           C. P = -207          D. P = 25

Câu 22. Tính khoảng cách d giữa hai điểm cực trị của đồ thị hàm số y = (x + 1)(x - 2)² 

A. d = 2√5 .           B. d = 2.              C. d = 4.             D. d = 5√2.

Câu 23. (ĐỀ CHÍNH THỨC 2016 – 2017) Đường cong ở hình bên là đồ thị của hàm số y = ax⁴ + bx² + c với a,b,c là các số thực. 

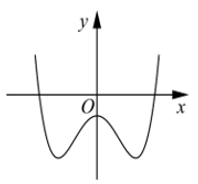
Mệnh đề nào dưới đây là đúng ?

A. Phương trình y^' = 0 vô nghiệm trên tập số thực.

B. Phương trình y^' = 0 có đúng một nghiệm thực.

C. Phương trình y^' = 0 có đúng hai nghiệm thực phân biệt.

D. Phương trình y^' = 0 có đúng ba nghiệm thực phân biệt.

Câu 24. Cho hàm số y = f(x) liên tục tại x₀ và có bảng biến thiên sau:

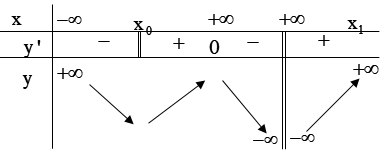
Mệnh đề nào sau đây là đúng?

A. Hàm số có hai điểm cực đại, một điểm cực tiểu.    

B. Hàm số có một điểm cực đại, không có điểm cực tiểu.

C. Hàm số có một điểm cực đại, hai điểm cực tiểu.    

D. Hàm số có một điểm cực đại, một điểm cực tiểu.

Câu 25*. Cho hàm số y = f(x) có bảng biến thiên sau:

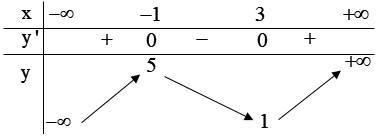
Hàm số y = |f(x)| có bao nhiêu điểm cực trị ? 

A. 5                    B. 3                   C. 4                    D. 2 

Câu 26. (ĐỀ THPT QG 2017)  Đồ thị của hàm số y = x³ – 3x² – 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?

A. P(1,0)                     B. M(0,-1)             C. N(1,-10)               D. Q(-1,10) 

Câu 27. (ĐỀ THPT QG 2017)  Đồ thị của hàm số y = – x³ + 3x² + 5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.

Câu 28. Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x - 2)² là:

A. 2√5 .              B. 2.                    C. 4.                   D. 5√2 .

Câu 29. Trong các đường thẳng dưới đây, đường thẳng nào đi qua trung điểm đoạn thẳng nối các điểm cực trị của đồ thị hàm số y = x³ - 3x² + 1 ?

Câu 30. Đồ thị hàm số x⁴ - x² + 1 có bao nhiêu điểm cực trị có tung độ dương?

A. 1.                   B. 2.                    C. 3.                   D. 4.

Câu 31. Cho hàm số f(x) = (x² - 3)². Giá trị cực đại của hàm số f^'(x) bằng:

A. 8.                   B. -8 .                 C. 0.                   D.  .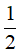

Câu 32. Điểm cực trị của hàm số y = sin2x - x là:

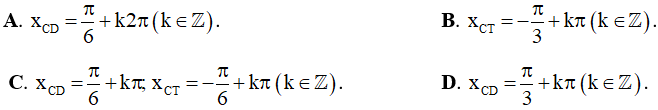
Câu 33. Giá trị cực đại của hàm số y = x + 2cosx trên khoảng (0;π) là:

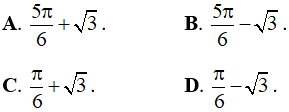
Câu 34. Cho hàm số y = sinx - √3cosx. Khẳng định nào sau đây sai:

A. 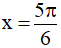 là một nghiệm của phương trình.

B. Trên khoảng (0;π) hàm số có duy nhất một cực trị.

C. Hàm số đạt cực tiểu tại .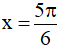

D. y + y^'' = 0, ∀x ∈ R .

Câu 35. Độ giảm huyết áp của một bệnh nhân được đo bởi công thức G(x) = 0,025x² (30 - x) trong đó x(mg) và x > 0 là liều lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng:

A. 15mg.                      B. 30mg.                C. 40mg.                        D. 20mg. 

Câu 36. Hỏi hàm số y = |x|³ - 3x + 1 có tất cả bao nhiêu điểm cực trị?

A. Không có điểm cực trị.             B. Có một điểm cực trị.

C. Có hai điểm cực trị.                  D. Có ba điểm cực trị.

Đáp án

 

Dạng 2: Tìm điều kiện để hàm số có cực trị. 

1. Phương pháp. Sử dụng định lí 2 và định lí 3

a, Cực trị của hàm số bậc ba:

Cho hàm số y = ax³ + bx² + cx + d, a ≠ 0.

y’ = 0 ⇔ 3ax² + 2bx + c = 0 (1) ; Δ’_y’ = b² – 3ac

 - Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.

→ Hàm số bậc 3 không có cực trị ⇔ b² – 3ac ≤ 0

 - Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.

→ Hàm số bậc 3 có 2 cực trị ⇔ b² – 3ac > 0

b, Cực trị của hàm số bậc bốn trùng phương:

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

y' = 4ax³ + 2bx;  y' = 0 ⇔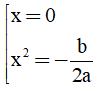 

- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Chú ý

* Hàm số f (xác định trên D) có cực trị ⇔ ∃x_o ∈D thỏa mãn hai điều kiện sau:

- Tại đạo hàm của hàm số tại x_o phải bằng 0 hoặc hàm số không có đạo hàm tại x_o

- f ‘(x) phải đổi dấu qua điểm x_o hoặc f ”(x_o) ≠ 0.

2. Ví dụ minh hoạ.

Ví dụ 1. Tìm tất cả các giá trị của tham số m để hàm số y = x³ - 3mx² + 6mx + m có hai điểm cực trị.

A. m ∈ (0;2) .                                      B. m ∈ (-∞;0) ∪ (8;+∞)          

C. m ∈ (-∞;0) ∪ (2;+∞)                       D. m ∈ (0;8) . 

Lời giải

Ta có y^' = 3x² - 6mx + 6m = 3(x² - 2mx + 2m) .

Để hàm số có hai điểm cực trị ⇔ x² - 2mx + 2m = 0 có hai nghiệm phân biệt 

 

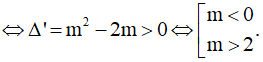
Chọn C.

Ví dụ 2. Cho hàm số y = ax⁴ + bx² + c (a ≠ 0). Với điều kiện nào của các tham số a,b,c thì hàm số có ba điểm cực trị?

A. a,b cùng dấu và c bất kì.     B. a,b trái dấu và c bất kì.

C. b = 0 và a,c bất kì.              D. c = 0 và a,b bất kì.

Lời giải

Ta có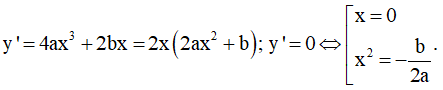  

Để hàm số có ba điểm cực trị 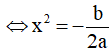 có hai nghiệm phân biệt khác 0  

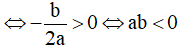. Khi đó a,b trái dấu và c bất kì.

Chọn B.

Ví dụ 3. Tìm tất cả các giá trị thực của tham số m để hàm số y = mx⁴ + (m + 1)x² + 1 có một điểm cực tiểu.

A. m > 0               B. m ≥ 0              C. -1 < m < 0                  D. m > -1

Lời giải 

TH1. Với a = 0 ⇔ m = 0, khi đó y = x² + 1 có đồ thị là một parabol có bề lõm quay lên nên hàm số có duy nhất một điểm cực tiểu.

→ m = 0 thỏa mãn.

TH2. Với a > 0 ⇔ m > 0  (*),

Yêu cầu bài toán ⇔ ab ≥ 0 ⇔ m(m + 1) ≥ 0 

Ta có: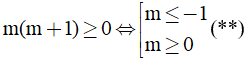 

Từ (*), (**)  → m > 0 thỏa mãn.

TH3. Với a > 0 ⇔ m < 0

yêu cầu bài toán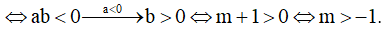 

→ -1 < m < 0 thỏa mãn.

Hợp các trường hợp ta được m > -1 . 

Chọn D.

Nhận xét. Bài toán hỏi hàm số có một điểm cực tiểu nên hàm số có thể có điểm cực đại hoặc không có điểm cực đại. Khi nào bài toán hỏi hàm số có đúng một cực tiểu và không có cực đại thì lúc đó ta chọn đáp án B.

Ví dụ 4. Cho hàm số 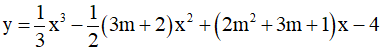. Tìm giá trị thực của tham số m để hàm số có hai điểm cực trị là x = 3 và x = 5.

A. m = 0 .              B. m = 1 .               C. m = 2.              D. m = 3.

Lời giải

Ta có y^' = x² - (3m + 2)x + (2m² + 3m + 1).

Yêu cầu bài toán ⇔ y^' có hai nghiệm x = 3 hoặc x = 5.

Thay x = 3 và x = 5 vào y’ ta có hệ phương trình:

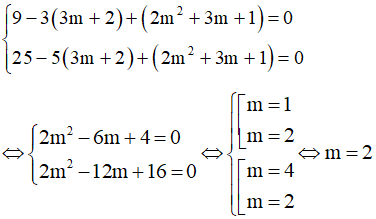
Chọn C.

Ví dụ 5. Cho hàm số y = 2x³ + bx² + cx + 1 Biết M(1;-6) là điểm cực tiểu của đồ thị hàm số. Tìm toạ độ điểm cực đại N của đồ thị hàm số.

A. N(2;21)          B. N(-2;21)         C. N(-2;11)         D. N(2;6) 

Lời giải

Đạo hàm y^' = 6x² + 2bx + c và y^'' = 12x + 12b .

Điểm M(1;-6) là điểm cực tiểu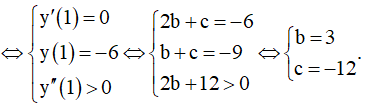  

Khi đó y = f(x) = 2x³ + 3x² -12x + 1 . 

Ta có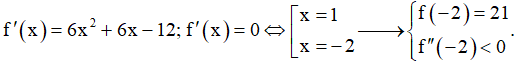  

Suy ra N(-2;21) là điểm cực đại của đồ thị hàm số. 

Chọn B. 

3. Bài tập tự luyện.

Câu 1. Hàm số y = x³ - (m + 2)x + m đạt cực tiểu tại x = 1 khi:

A. m = -1            B. m = 2               C. m = -2            D. m = 1 

Câu 2. Tìm giá trị thực của tham số m để hàm số y = x³ - 3x² + mx đạt cực đại tại x = 0 

A. m = 1                B. m = 2                C. m = -2               D. m = 0

Câu 3.  Biết rằng đồ thị hàm số y = ax⁴ + bx² + c (a ≠ 0) có điểm đại A(0;-3) và có điểm cực tiểu B(-1;-5). Mệnh đề nào sau đây là đúng?

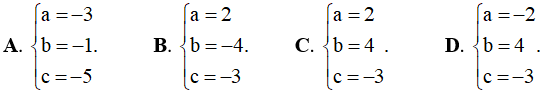
Câu 4. Cho hàm số y = ax⁴ + bx² + c (a ≠ 0). Để hàm số có một cực tiểu và hai cực đại thì a, b  cần thỏa mãn: 

A. a < 0, b < 0 .      B. a < 0, b > 0      C. a > 0, b < 0.     D. a > 0, b > 0.

Câu 5. Cho hàm số y = ax⁴ + bx² + 1 (a ≠ 0). Để hàm số chỉ có một cực trị và là cực tiểu thì a, b cần thỏa mãn:

A. a < 0, b ≤ 0      B. a < 0, b > 0.      C. a > 0, b < 0.     D. a > 0, b ≥ 0

Câu 6. Hàm số y = ax⁴ + 2mx² + m² + m có ba cực trị khi:

A. m = 0              B. m > 0               C. m < 0               D. m ≠ 0 

Câu 7. Đồ thị hàm số y = x⁴ - 3x² + ax + b có điểm cực tiểu A(2;-2). Tìm tổng a + b.

A. - 14.                 B. 14.                    C. - 20.                  D. 34.

Câu 8. Đồ thị hàm số y = ax⁴ + bx² + c có điểm đại A(0;-3) và có điểm cực tiểu  B(-1; - 5). Khi đó giá trị của a, b, c  lần lượt là:

A. -3,-1,-5 .                   B. 2,-4,-3 .            C. 2,4,-3 .             D. -2,4,-3 .

Câu 9. Hàm số 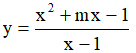 có cực đại và cực tiểu thì điều kiện của m là:

A. m < 0 .              B. m = 0 .              C. m ∈ R .              D. m > 0. 

Câu 10. Hàm số 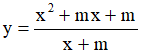 đạt cực đại tại x= 2 khi giá trị thực m bằng:

A. -1 .                   B. -3 .                    C. 1.                      D. 3 .

Câu 11. Hàm số y = sin3x + msinx đạt cực đại tại 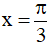 khi m bằng:

A. 5.                     B. -6 .                   C. 6.                     D. -5 . 

Câu 12. Biết hàm số y = asinx + bcosx + x (0 < x < 2π) đạt cực trị tại 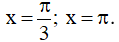 Khi đó tổng a + b bằng:

A. 3.                    B. 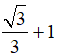C. √3 + 1 .              D. √3 - 1

Câu 13. Tìm tất cả các giá trị của tham số m để hàm số 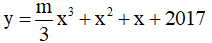 có cực trị.

A. m ∈ (-∞;1] .                          B. m ∈ (-∞;0] ∪ (0,1). 

C. m ∈ (-∞;0] ∪ (0,1].               D. m ∈ (-∞;1). 

Câu 14. Biết rằng hàm số y = (x + a)³ + (x + b)³ - x³ có hai điểm cực trị. Mệnh đề nào sau đây là đúng?

A. ab > 0 .              B. ab < 0              C. ab ≥ 0             D. ab ≤ 0

Câu 15. Tìm các giá trị của tham số m để hàm số y = (m - 3)x³ - 2mx² + 3 không có cực trị.

A. m = 3.              B. m = 3, m = 0.    C. m = 0.             D. m ≠ 3 .

Câu 16. Cho hàm số y = ax³ + bx² + cx + d. Biết M(0,2), N(2;-2) là các điểm cực trị của đồ thị hàm số. Tính giá trị của hàm số tại x = -2 .

A. y(-2) = 2 .       B. y(-2) = 22      C. y(-2) = 6.        D. y(-2) = -18

Câu 17. Biết rằng hàm số y = ax³ + bx² + cx (a ≠ 0) nhận x = -1 là một điểm cực trị. Mệnh đề nào sau đây là đúng?

A.  a + c = b .         B.  2a - b = 0 .       C. 3a + c = 2b  .     D. 3a + 2b + c = 0  .

Câu 18. Cho hàm số 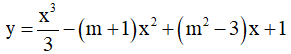 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số đạt cực trị tại x = -1 .

A. m = 0              B. m = -2            C. m = 0,m = -2.           D. m = 0,m = 2

Câu 19. Biết rằng hàm số y = 3x³ - mx² + mx - 3 có một điểm cực trị x₁ = -1. Tìm điểm cực trị còn lại x₂ của hàm số.

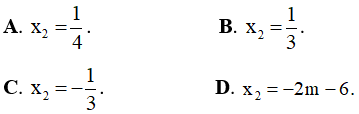
Câu 20. Cho hàm số y = x³ - 3mx² + 3(m² - 1)x - 3m² + 5 với m là tham số thực. Tìm tất cả các giá trị của x = 1 để hàm số đạt cực đại tại  .

A. m = 0,m = 2                     B. m = 2                      C. m = 1                     D. m = 0 

Câu 21. Hàm số y = x³ - 3mx² + 6mx + m có hai điểm cực trị khi m thỏa mãn điều kiện:

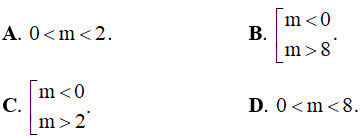
Câu 22. Hàm số 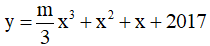 có cực trị khi và chỉ khi:

 

Câu 23. Với điều kiện nào của a và b để hàm số y = (x + a)³ + (x + b)³ - x³ đạt cực đại và cực tiểu ? 

A. ab >0.               B. ab < 0.               C. ab ≥ 0.              D. ab ≤ 0. 

Câu 24. Hàm số y = (m - 3)x³ - 2mx² + 3 không có cực trị khi: 

A. m = 3.               B. m = 0 hoặc m = 3.    C. m = 0.        D. m ≠3.

Câu 25. Tìm tất cả các giá trị của m để hàm số 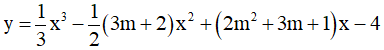 đạt cực trị tại x = 3 hoặc x = 5, ta được.

A. m = 0.               B. m = 1.               C. m = 2.               D. m = 3.

Câu 26. (ĐỀ THPT QG 2017) Tìm giá trị thực của tham số m để hàm số 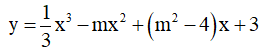 đạt cực đại tại x = 3.

A. m = 0.               B. m = 3.               C. m = 5.              D. m = 1.

Câu 27. Tìm tất cả các giá trị thực của tham số m để hàm số y = x⁴ + 2mx² + m² + m có ba điểm cực trị.

A. m = 0              B. m > 0               C. m < 0              D. m ≠ 0 

Câu 28. Tìm tất cả các giá trị của tham số m để hàm số y = mx⁴ + (m - 1)x² + 1 - 2m có đúng một điểm cực trị.

A. m ∈ [1;+∞) .                         B. m ∈ (-∞;0]    

C. m ∈ [0;1]                              D. m ∈ (-∞;0] ∪ [1;+∞)

Câu 29. Cho hàm số y = x³ - 3x² - 9x + m. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.

A. y = -8x + m .                         B. y = -8x + m - 3                  

C. y = -8x + m + 3 .                   D. y = -8x - m + 3

Câu 30. Biết rằng đồ thị hàm số y = x⁴ - 3x² + ax + b có điểm cực tiểu là A(2;-2). Tính tổng S = a + b 

A. S = -14 .           B. S = 14               C. S = -20.            D. S = 34

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
D	D	B	B	D	C	A	B	D	B	C	C	D	A	C
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
D	C	A	B	B	C	D	A	C	C	C	C	D	B	B

 

Dạng 3: Tìm điều kiện để các điểm cực trị của hàm số thỏa mãn điều kiện cho trước.

1. Phương pháp giải.

a, Hàm số bậc ba y = ax³ + bx² + cx + d (a ≠ 0, a, b, c, d phụ thuộc vào tham số)
 Bước 1: Tính y’ = 3ax² + 2bx + c, y’ = 0  ⇔ 3ax² +2bx + c = 0 (1)

Để hàm số có cực đại, cực tiểu  ⇔ y’ = 0 có hai nghiệm phân biệt  

⇔ (1) có hai nghiệm phân biệt

⇔ Giá trị tham số thuộc miền D nào đó (*)

Bước 2: Từ điều kiện cho trước dẫn tới một phương trình hoặc một bất phương trình theo tham số, giải phương trình này ta được tham số sau đó đối chiếu với điều kiện (*) và kết luận.

Một số điều kiện thường gặp: (Không dùng dấu tương đương như vậy)

- Để hàm số y = f(x) có 2 cực trị ⇔ a ≠ 0, Δy′ > 0 hoặc a ≠ 0, Δ_y′ > 0 

- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục hoành ⇔ y_CD.y_CT  < 0 

- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục tung ⇔x_CD.x_CT < 0

- Để hàm số y = f(x) có 2 cực trị nằm phía trên trục hoành ⇔y_CD+y_CT > 0 và y_CD.y_CT > 0

- Để hàm số  y = f(x) có 2 cực trị nằm phía dưới trục hoành ⇔y_CD+y_CT < 0 và y_CD.y_CT > 0

- Để hàm số  y = f(x) có cực trị tiếp xúc với trục hoành ⇔y_CD.y_CT = 0

- Đồ thị có 2 điểm cực trị khác phía đối với đường thẳng d: Ax + By + C = 0

+ Gọi M₁(x₁; y₁) và M₂(x₂; y₂) là cực đại và cực tiểu của đồ thị hàm số.

+ Gọi t₁ và t₂ là các giá trị khi thay M₁ và M₂ vào đường thẳng d:

t₁ = Ax₁ + By₁ + C; t₂ = Ax₂ + By₂ + C

+ Đồ thị có 2 điểm cực đại, cực tiểu nằm ở hai phía của đường thẳng d:

⇔ y′ = 0 có 2 nghiệm phân biệt và t₁t₂ < 0

+ Đồ thị có 2 điểm cực đại, cực tiểu nằm ở cùng một phía của đường thẳng d:

⇔ y′ = 0 có 2 nghiệm phân biệt và t₁t₂ > 0

Chú ý: Khi thay đường thẳng d bằng trục Ox, Oy hoặc đường tròn thì vẫn áp dụng kết quả trên. Với các điều kiện khác thì tuỳ từng trường hợp.

b, Hàm trùng phương y = ax⁴ + bx² + c. Khi đó:

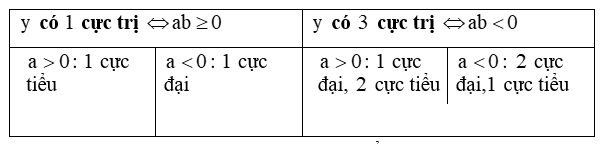
- Xét trường hợp có ba cực trị → toạ độ các điểm cực trị

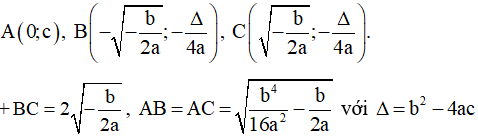
+ Phương trình qua điểm cực trị: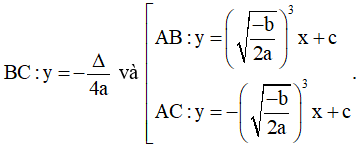 

+ Gọi 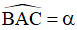, luôn có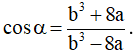 

+ Diện tích tam giác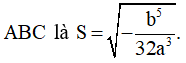 

+ Bán kính đường tròn ngoại tiếp tam giác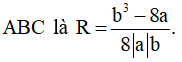 

+ Bán kính đường tròn nội tiếp tam giác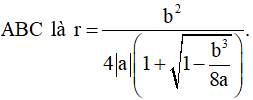 

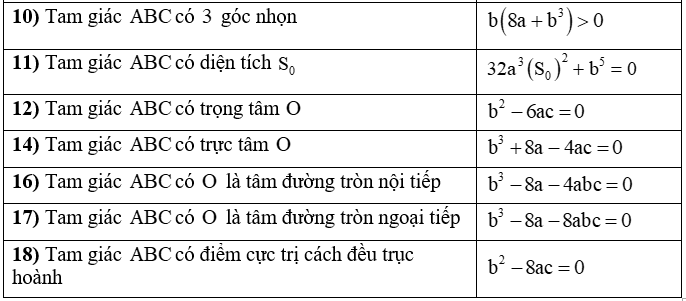
+ Đồ thị hàm số y = ax⁴ + bx² + c cắt trục hoành tại 4 điểm lập thành một cấp số cộng thì điều kiện là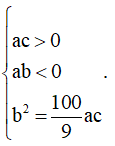  

2. Ví dụ minh hoạ.

Ví dụ 1. (ĐỀ CHÍNH THỨC 2016 – 2017) Tìm giá trị thực của tham số m để đường thẳng d: y = (2m - 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x³ - 3x² + 1 .

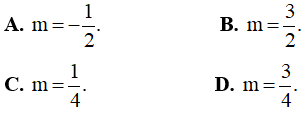
Lời giải

Xét hàm y = x³ - 3x² + 1 , có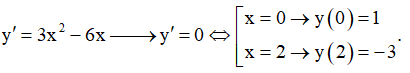  

Suy ra A(0;1), B(2,-3) là hai điểm cực trị của đồ thị hàm số.

Suy ra đường thẳng AB có một VTCP là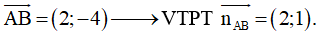  

Đường thẳng d: y = (2m - 1)x + 3 + m có một VTCP là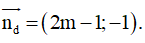  

Yêu cầu bài toán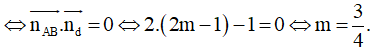  

Chọn D.

Ví dụ 2. Cho hàm số 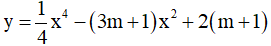 với m là tham số thực. Tìm giá trị của  để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ.

Lời giải

Ta có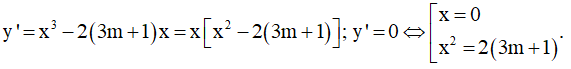  

Để hàm số có ba điểm cực trị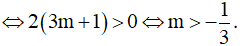  

Khi đó đồ thị hàm số có ba điểm cực trị là:

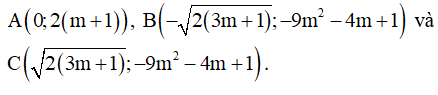
Suy ra toạ độ trọng tâm của tam giác ABC là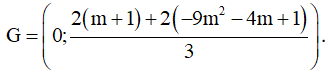  

Yêu cầu bài toán: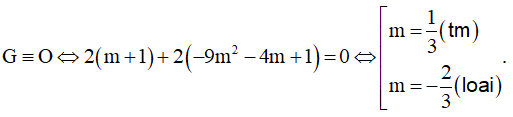  

Chọn D.

Cách áp dụng công thức giải nhanh: Điều kiện để có ba cực trị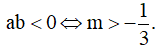  

Yêu cầu bài toán: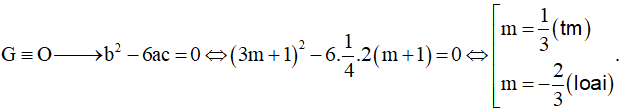 

3. Bài tập tự luyện.

Câu 1. Tìm m để đồ thị hàm số y = x⁴ - 2(m² - m + 1)x² + m -1 có một điểm cực đại, hai điểm cực tiểu và thỏa mãn khoảng cách giữa hai điểm cực tiểu ngắn nhất.

Câu 2. Cho hàm số y = -x⁴ + 2mx² - 4 có đồ thị là (C_m). Tìm các giá trị của m để tất cả các điểm cực trị của (C_m) đều nằm trên các trục tọa độ.

A. m ≤ 0 .              B. m = 2.               C. m > 0 .              D. m ≤ 0 hoặc m = 2 .

Câu 3. Giá trị của tham số m bằng bao nhiêu để đồ thị hàm số y = x⁴ - 2mx² + 1 có ba điểm cực trị A(0;1), B, C thỏa mãn BC = 4?

A. m = ±4 .            B. m = √2 .            C. m = 4 .              D. m = ±√2 . 

Câu 4. Cho hàm số y = x⁴ - 2(m + 1)x² + m², với m là tham số thực. Tìm m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.

A. m = -1               B. m = 0               C. m = 1              D. Đáp án khác.

Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x⁴ + 2mx² + 1 có ba điểm cực trị tạo thành tam giác vuông cân.

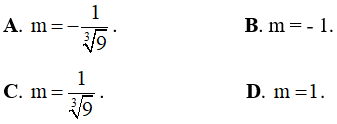
Câu 6. Tìm m để đồ thị hàm số 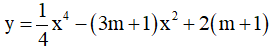 có ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ.

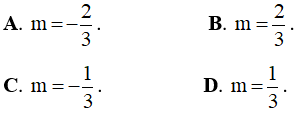
Câu 7. (ĐỀ THPT QG 2017)  Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x⁴ - 2mx² có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

A. m > 0                B. m < 1                 C. 0 < m < ³√4        D. 0 < m < 1 

Câu 8. Tìm tất cả các giá trị của tham số m để hàm số f(x) = 2x³ - 3x² - m có các giá trị cực trị trái dấu:

A. – 1 và 0.            B. (-∞;0) và (-1;+ ∞).           C. (-1;0).                  D. [0;1].

Câu 9. Cho hàm số y = 2x³ - 3(m + 1)x² + 6mx + m³. Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho độ dài AB = √2. 

A. m = 0.               B. m = 0 hoặc m = 2            C. m = 1.                   D. m = 2.

Câu 10. Gọi x₁, x₂ là hai điểm cực trị của hàm số y = x³ - 3mx² + 3(m² - 1)x - m³ + m. Giá trị của m để x₁² + x₂² - x₁ x₂ = 7 là: 

Câu 11. (ĐỀ THPT QG 2017) Tìm giá trị thực của tham số m để đường thẳng d: y = (2m - 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của hàm số y = x³ - 3x² + 1 . 

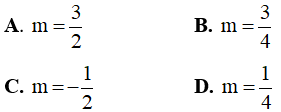
Câu 12. (ĐỀ THPT QG 2017)  Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x³ – 3mx² + 4m³ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ. 

A. 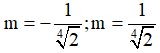                B. m = -1,m = 1     

C. m = 1                                            D. m ≠ 0 

Câu 13. Nếu x = 1 là hoành độ trung điểm của đoạn thẳng nối hai điểm cực đại, cực tiểu của đồ thị hàm số 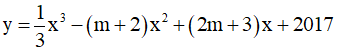 thì tập tất cả các giá trị của m là:

A. m = -1.              B. m ≠ -1.              C. 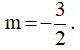. D. Không có giá trị m.

Câu 14. Giá trị của m để khoảng cách từ điểm M(0;3) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 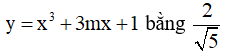 là:

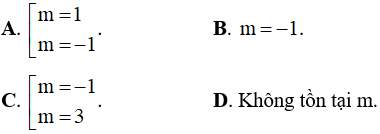
Câu 15. Cho hàm số y = 2x³ + 3(m - 1)x² + 6(m - 2)x - 1. Xác định m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2;3).

A. m ∈ (-1;3) ∪ (3;4) .              B. m ∈ (1;3)                  

C. m ∈ (3;4)                             D. m ∈ (-1;4)

Câu 16. Để hàm số y = x³ + 6x² + 3(m + 2)x - m - 6 có cực đại, cực tiểu tại x₁,x₂ sao cho x₁ < -1 < x₂ thì giá trị của m là:

A. m > 1 .               B. m < 1               C. m > -1            D. m < -1

Câu 17. Tìm tất cả các giá trị của tham số m để hàm số 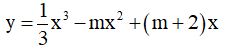 có hai điểm cực trị nằm trong khoảng (0;+∞)?

A. m > 2.               B. m < 2.               C. m = 2.               D. 0 < m < 2.

Câu 18. Với các giá trị nào của m thì hàm số y = x³ - 3x² + 3mx + 1 có các điểm cực trị nhỏ hơn 2?

A. m > 0             B. m < 1 .               C. 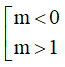D. 0 < m < 1 .

Câu 19. Cho hàm số y = 2x³ - 3(2a + 1)x² + 6a(a + 1)x + 2. Nếu gọi x₁, x₂ lần lượt là hoành độ các điểm cực trị của đồ thị hàm số thì giá trị |x₁ – x₂| bằng:

A. a + 1.                B. a.                      C. a – 1.                 D. 1.

Câu 20. Cho hàm số y = 2x³ + mx² -12x - 13. Với giá trị nào của m thì đồ thị hàm số có điểm cực đại, cực tiểu cách đều trục tung ? 

A. 2.                      B. - 1.                    C. 1.                     D. 0.

Câu 21. Đồ thị hàm số y = -x³ + 3mx² - 3m - 1 có hai điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng d: x + 8y - 74 = 0 thì tập tất cả các giá trị của m: 

A. m = 1.               B. m = -2            C. m = -1             D. m = 2

Câu 22. Cho hàm số y = x³ + 3x² + mx + m -2 với m là tham số, có đồ thị là (C_m). Xác định m để (C_m) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành ? 

A. m < 2 .              B. m ≤ 3               C. m < 3              D. m ≤ 2 

Câu 23. Cho hàm số 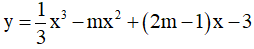 với m là tham số, có đồ thị là (C_m). Xác định m để (C_m) có các điểm cực đại và cực tiểu nằm về cùng một phía đối với trục tung ? 

Câu 24. Hàm số y = ax³ + bx² + cx + d đạt cực trị tại x₁, x₂ nằm hai phía trục tung khi và chỉ khi:

A. a > 0, b < 0, c > 0 .     B. a và c trái dấu. 

C. b² - 12ac ≥ 0 .             D. b² - 12ac > 0

Câu 25. Cho hàm số y = x³ - 3mx² + 4m² - 2. Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho I(1;0) là trung điểm của AB.

A. m = 0 .              B. m = -1.             C. m = 1               D. m = 2 

Câu 26. Với giá trị nào của tham số m thì đồ thị hàm số y = x³ - 3mx² + 2 có hai điểm cực trị A, B sao cho A, B và M(1;-2) thẳng hàng. 

A. m = 0              B. m = √2            C. m = -√2                  D. m = ±√2

Câu 27. Với giá trị nào của tham số m thì đồ thị hàm số y = -x³ - 3mx + 1 có hai điểm cực trị A, B sao cho tam giác OAB vuông tại O, với O là gốc tọa độ ?

A. m = -1             B. m > 0                C. 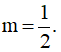D. m = 0 

Câu 28. Cho hàm số y = x³ - 3x² - mx + 2 với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng d: x + 4y - 5 = 0 một góc α = 45⁰ 

Câu 29. Cho hàm số y = x⁴ - 2mx² + 2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có ba điểm cực trị A,B,C thỏa mãn OA.OB.OC = 12 với O là gốc toạ độ?

A. 2                     B. 1                     C. 0                     D. 4 

Câu 30. Cho hàm số y = -x⁴ + 2mx² - 4 có đồ thị là (C_m). Tìm tất cả các giá trị thực của tham số m để tất cả các điểm cực trị của (C_m) đều nằm trên các trục tọa độ.

A. m = ±2 .                      B. m = 2    

C. m > 0 .                        D. m = 2, m > 0 .

Câu 31. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x⁴ - 2mx² + 1 có ba điểm cực trị A(0;1), B, C thỏa mãn BC = 4.

A. m = ±4 .            B. m = √2            C. m = 4              D. m = ±√2 . 

Câu 32. Cho hàm số y = x⁴ - 2(m + 1)x² + m² với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.

A. m = -1.             B. m = 0.               C. m = 1.               D. m > -1.

Câu 33. (ĐỀ MINH HỌA 2016 – 2017) Tìm giá trị thực của tham số m sao cho đồ thị của hàm số y = x⁴ + 2mx² + 1 có ba điểm cực trị tạo thành tam giác vuông cân.

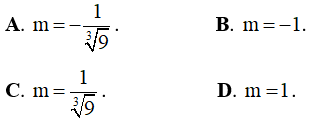
Câu 34. Cho hàm số y = 3x⁴ + 2(m - 2018)x² + 2017 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng 120⁰. 

A. m = -2018               B. m = -2017                C. m = 2017             D. m = 2018 

Câu 35. (ĐỀ CHÍNH THỨC 2016 – 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x⁴ - 2mx² có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

A. m > 0               B. m < 1                C. 0 < m < ³√4       D. 0 < m < 1 

Câu 36. Cho hàm số y = x⁴ - mx² + m - 1 với m là tham số thực. Tìm giá trị của   để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn nội tiếp bằng 1 

A. m = -2              B. m = 1                C. m = 2               D. m = 4 

 

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
B	B	C	B	B	D	D	C	B	B	B	B	D	B	A	B	A	D
19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
D	D	D	C	C	B	C	D	C	A	B	B	C	B	B	C	D	D

Phần 3: Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số

A. LÝ THUYẾT.

1. Định nghĩa.

Giả sử hàm số f(x) xác định trên tập K (K ⊂ R) Khi đó:

a)  Nếu tồn tại một điểm x₀ ∈ K sao cho f(x) ≤ f(x₀), ∀x ∈ K thì số M = f(x₀) được gọi là giá trị lớn nhất của hàm số f(x) trên K. Kí hiệu: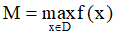 

b)  Nếu tồn tại một điểm x₀ ∈ K sao cho f(x) ≥ f(x₀), ∀x ∈ K thì số m = f(x₀) được gọi là giá trị nhỏ nhất của hàm số f(x) trên K. Kí hiệu: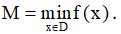 

2. Nhận xét.

- Như vậy để có được M (hoặc m) là giá trị lớn nhất (giá trị nhỏ nhất) của hàm số f(x) trên K ta phải chỉ ra được :

a) f(x) ≤ M (hoặc f(x) ≥ M) với mọi x ∈ K.

b) Tồn tại ít nhất một điểm x₀ ∈ K sao cho f(x₀) = M (hoặc f(x₀) = m).

- Chú ý khi nói đến giá trị lớn nhất hay giá trị nhỏ nhất của hàm số f(x) (mà không nói rõ “trên tập K’’) thì ta hiểu đó là giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.

- Mỗi hàm số liên tục trên đoạn [a;b] thì đạt được giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

Hơn nữa:

a) Nếu hàm số f(x) đồng biến trên đoạn [a;b] thì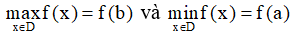 

b) Nếu hàm số f(x) nghịch biến trên đoạn [a;b] thì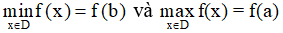 

- Cho phương trình f(x) = m với y = f(x) là hàm số liên tục trên D thì phương trình có nghiệm khi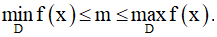 

- Một hàm số có thể đồng thời đạt được giá trị lớn nhất và giá trị nhỏ nhất trên một tập K hoặc chỉ đạt được giá trị nhỏ nhất hoặc chỉ đạt được giá trị lớn nhất hoặc không tồn tại cả hai giá trị này. Chẳng hạn:

a) Xét hàm số bậc hai y = ax² + bx + c trên tập xác định K = R .

+ Khi a > 0 thì hàm số có đạt được giá trị nhỏ nhất tại 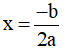 đồng thời bằng giá trị cực tiểu của hàm số tại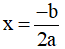 

 + Khi a < 0 thì hàm số có đạt được giá trị lớn nhất tại 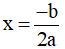 đồng thời bằng giá trị cực đại của hàm số tại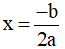 

b) Xét trên tập K = R hàm số bậc ba y = ax³ + bx² + cx + d không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.

c) Xét trên 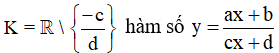 không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.

d) Xét hàm số trùng phương y = ax⁴ + bx² + c trên tập xác định K = R .

+ Khi a > 0 thì hàm số đạt được giá trị nhỏ nhất đồng thời bằng giá trị cực tiểu của hàm số.

+ Khi a < 0 thì hàm số đạt được giá trị lớn nhất đồng thời bằng giá trị cực đại của hàm số.

B. CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Tìm GTLN, GTNN của hàm số trên 1 đoạn.

1. Phương pháp giải.

Phương pháp: Cho hàm số y = f(x) xác định và liên tục trên [a,b] .

Bước 1. Tính đạo hàm f'(x) .

Bước 2. Tìm tất cả các nghiệm x_i ∈ [a,b] của phương trình f'(x) = 0 và tất cả các điểm α_i ∈ [a,b] làm cho f'(x) không xác định.

Bước 3. Tính f(a), f(b), f(x_i), f(α_i).

Bước 4. So sánh các giá trị tính được và kết luận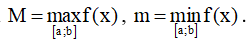 

Lưu ý: 

- Đối với bài toán tìm GTLN, GTNN trên khoảng, nửa đoạn làm tương tự. 

- Trong trường hợp trên khoảng đó không tồn tại giá trị f’(x) = 0 hoặc không xác định thì kết luận không tìm được GTLN, GTNN trên khoảng đó.

- Đối với bài toán xét trên cả tập xác định, tham khảo phần A.5 Lý thuyết.

2. Ví dụ minh hoạ.

Ví dụ 1. Giá trị nhỏ nhất của hàm số f(x) = x⁴ - 10x² - 2 trên đoạn [0;9] bằng:

A. -2 .                 B. -11.                  C. -26 .                  D. -27 .

Lời giải

Ta có f'(x) = 4x³ - 20x 

   

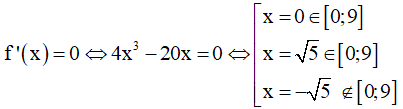
f(0) = -2; f(√5) = -27; f(9) = 5749 .

Vậy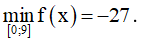 

Chọn D.

Ví dụ 2. Trên đoạn [-2;1], hàm số y = x³ - 3x² - 1 đạt giá trị lớn nhất tại điểm:

A. x = -2.                    B. x = 0 .                C. x = -1 .                      D. x = 1 .

Lời giải

Đặt y = f(x) = x³ – 3x² – 1 

Ta có 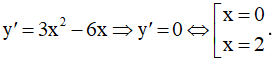 Ta đang xét trên đoạn [-2;1] nên loại x = 2

Ta có f(-2) = -21; f(0) = -1; f(1) = -3. Do đó giá trị lớn nhất của hàm số trên đoạn [-2;1] là –1, tại x = 0.

Chọn B.

Ví dụ 3. Tìm giá trị lớn nhất M của hàm số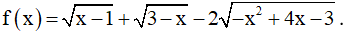 

A. M = 0              B. M = - √2          C. M = √2          D.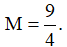  

Lời giải 

TXĐ: D = [1;3] Đặt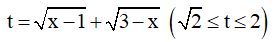  

 

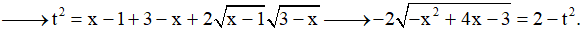
Khi đó, bài toán trở thành ''Tìm giá trị lớn nhất của hàm số g(t) = -t² + t + 2 trên đoạn [√2;2]''.

Xét hàm số g(t) = -t² + t + 2 xác định và liên tục trên [√2;2]  

Đạo hàm g'(t) = -2t + 1 < 0,∀t ∈ (√2;2) .

Suy ra hàm số g(t) nghịch biến trên đoạn [√2;2] 

Do đó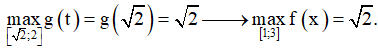  

Chọn C.

Ta có: 

Từ phép đặt ẩn phụ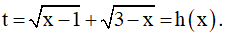 

Đạo hàm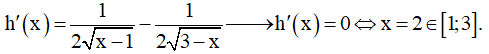  

Ta có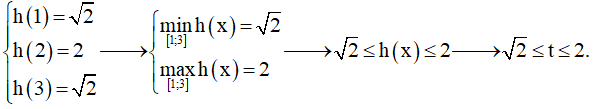  

Ví dụ 4. Tìm giá trị lớn nhất M của hàm số f(x) = |-x² - 4x + 5| trên đoạn [-6;6] .

A. M = 0             B. M = 9          C. M = 55          D. M = 110 

Lời giải

Xét hàm số g(x) = -x² - 4x + 5 liên tục trên đoạn [-6;6]. 

Đạo hàm g'(x) = -2x - 4 → g'(x) = 0 ⇔ x = -2 ∈ [-6;6]

Lại có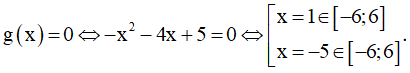 

Ta có 

 

 

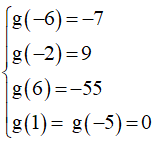
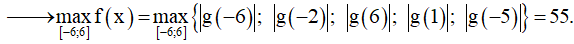
Chọn C.

Lưu ý: Hàm trị tuyệt đối không âm.

Ví dụ 5. Tìm giá trị nhỏ nhất m của hàm số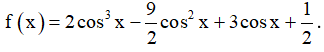 

A. m = -24         B. m = -12       C. m = -9          D. m = 1 

Lời giải

Đặt t = cosx (-1 ≤ t ≤ 1) 

Khi đó, bài toán trở thành ''Tìm giá trị nhỏ nhất của hàm số 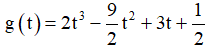 trên đoạn [-1;1] ''.

Đạo hàm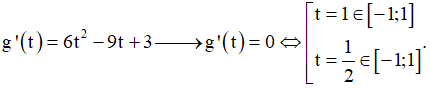  

Ta có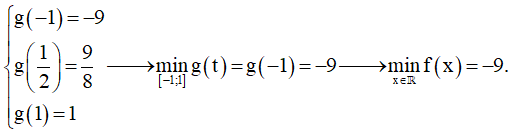  

Chọn C.

Ví dụ 6. Giá trị lớn nhất của hàm số 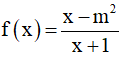 trên đoạn [0,1] bằng:

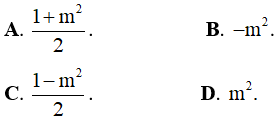
Lời giải

Đạo hàm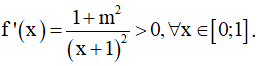 

Suy ra hàm số f(x) đồng biến trên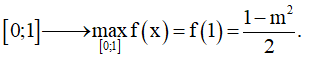  

Chọn C.

                                   

3. Bài tập tự luyện.

Câu 1. Giá trị nhỏ nhất của hàm số f(x) = x³ - 21x trên đoạn [2;19] bằng:

A. 36.                    B. -14√7 .              C. 14√7                 D. -34.

Câu 2. Giá trị nhỏ nhất của hàm số f(x) = x³ - 24x trên đoạn [2;19] bằng: 

A. 32√2 .               B. -40.                 C. -32√2 .            D. -45.

Câu 3. Tìm giá trị lớn nhất M của hàm số y = x⁴ - 2x² + 3 trên đoạn [0;√3] :

A. 3.                            B. -6.                   C. 10.                        D. 6.

Câu 4. Tìm giá trị nhỏ nhất m của hàm số y = x⁴ - x² + 13 trên đoạn [0;4]:

Câu 5. Tìm giá trị nhỏ nhất m của 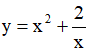 trên đoạn .

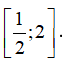Câu 6. Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = 2x³ + 3x² - 1 trên đoạn 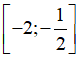. Tính P = M - N .

A. P = -5 .           B. P = 1 .            C.  P = 4.             D.  P = 5.

Câu 7. Xét hàm số 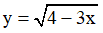 trên đoạn [-1,1]. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên đoạn [-1,1] . 

B. Hàm số có cực trị trên khoảng (-1,1) .

C. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-1,1] . 

D. Hàm số có giá trị nhỏ nhất bằng 1 khi x = 1, giá trị lớn nhất bằng √7 khi x = - 1.

Câu 8. Khi tìm giá trị lớn nhất và nhỏ nhất của hàm số 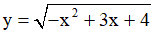, một học sinh làm như sau:

(1). Tập xác định D = [-1,4] và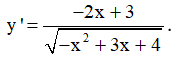 

(2). Hàm số không có đạo hàm tại x = -1; x = 4 và ∀x ∈ (-1;4) : y' = 0 ⇔  .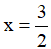

(3). Kết luận: Giá trị lớn nhất của hàm số bằng 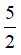 khi 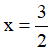 và giá trị nhỏ nhất bằng 0 khi x = -1; x = 4.

Cách giải trên:

A. Sai ở bước (3).                          B. Sai từ bước (1).

C. Sai từ bước (2).                         D. Cả ba bước  (1), (2), (3) đều đúng.

Câu 9. Khi tìm giá trị lớn nhất và nhỏ nhất của hàm số 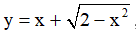, một học sinh làm như sau:

 (1). Tập xác định: D = [-√2;√2] và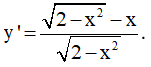 

 (2). 

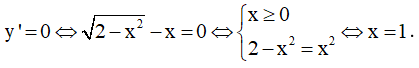
 (3). Kết luận: Giá trị lớn nhất của hàm số bằng 2 khi x = 1 và giá trị nhỏ nhất bằng -√2 khi x = -√2.

Cách giải trên:

A. Sai từ bước (1).                         B. Sai từ bước (2).

C. Sai ở bước (3).                          D. Cả ba bước (1), (2), (3) đều đúng

Câu 10. Tìm giá trị nhỏ nhất của hàm số 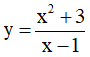 trên đoạn [2;4].

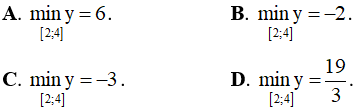
Câu 11. Giá trị lớn nhất của hàm số f(x) = |x² - 3x + 2| - x trên đoạn [-4;4] bằng:

A. 2.                   B. 17.                  C. 34.                 D. 68. 

Câu 12. Trên nửa khoảng [0;+∞), hàm số f(x) = x³ + x - cosx - 4 :

A. Có giá trị lớn nhất là - 5, không có giá trị nhỏ nhất.

B. Không có giá trị lớn nhất, có giá trị nhỏ nhất là - 5.

C. Có giá trị lớn nhất là -5, giá trị nhỏ nhất là - 5.

D. Không có giá trị lớn nhất, không có giá trị nhỏ nhất.

Câu 13. Hàm số nào sau đây không có giá trị nhỏ nhất và giá trị lớn nhất trên [-2;2] 

A. y = x³ + 2 .             B. y = x⁴ + x² .            C. 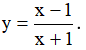D. y = -x + 1 .

Câu 14. Biết rằng hàm số f(x) = x³ - 3x² - 9x + 28 đạt giá trị nhỏ nhất trên đoạn [0;4] tại x₀. Tính P = x₀ + 2018 

A. P = 3                 B. P = 2019               C. P = 2021            D. P = 2018 

Câu 15. Tìm giá trị nhỏ nhất của hàm số 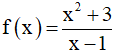 trên đoạn [2;4].

Câu 16. Tập giá trị của hàm số 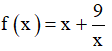 với x ∈ [2;4] là đoạn [a,b]. Tính P = b - a .

Câu 17. Cho hàm số 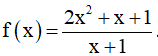. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [0;1]

A. M = √2; m = 1                                                    B. M = 2; m = 1          

C. M = 1; m = -2                                                     D. M = 2; m = √2 

Câu 18. Cho hàm số y = f(x) và có bảng biến thiên trên [-5;7) như sau: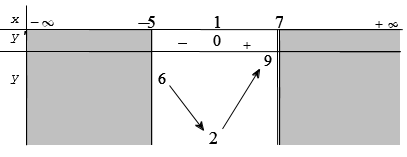

Mệnh đề nào sau đây là đúng?

A. 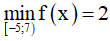 và hàm số không đạt giá trị lớn nhất trên [-5;7) .

B.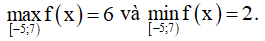  

C.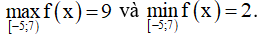 

D.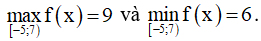 

Câu 19. Cho hàm số y = f(x) có đồ thị trên đoạn [-2;4] như hình vẽ. Tìm giá trị lớn nhất M của hàm số y = |f(x)| trên đoạn [-2;4] 

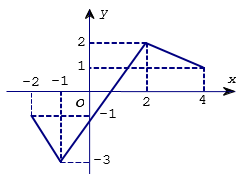
A. M = 2                                      C. M = 3

B. M = |f(0)|                                 D. M = 1 

Câu 20. Cho hàm số y = f(x) xác định và liên tục trên R, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn [-2;2].

 

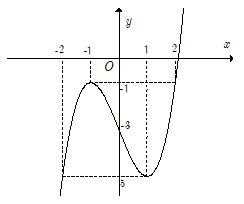
A. m = -5; M = 0                          C. m = -1; M = 0 

B. m = -5; M = -1                         D. m = -2; M = 2       

Câu 21. Tìm giá trị lớn nhất M của hàm số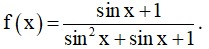 

Câu 22. Tìm giá trị lớn nhất M của hàm số f(x) = sin³x + cos2x + sinx + 3.

A. M = 0             B. M = 5          C. M = 4            D. M =  

Câu 23. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau: 

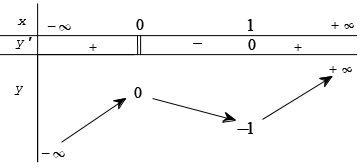
Khẳng định nào sau đây là đúng ? 

A. Hàm số có đúng một cực trị. 

B. Hàm số có giá trị cực tiểu bằng 1.

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 .

Câu 24. Tìm giá trị thực của tham số a để hàm số f(x) = -x³ - 3x² + a có giá trị nhỏ nhất trên đoạn [-1;1] bằng 0 

A. a = 2               B. a = 6.            C. a = 0              D. a = 4.

Câu 25. Giá trị lớn nhất của hàm số 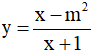 trên [0;1] bằng:

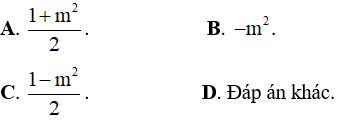
Câu 26. Cho hàm số f(x) = x³ + (m² + 1)x + m² -2 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0;2] bằng 7 

A. m = ±1 .          B. m = ±√7.      C. m = ±√2 .       D. m = ±3.

Câu 27. Cho hàm số 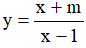 (với m là tham số thực) thỏa mãn 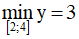. Mệnh đề nào dưới đây là đúng?

A. 3 < m ≤ 4        B. 1 ≤ m < 3        C. m > 4             D. m < -1 

Câu 28. Cho hàm số 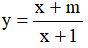 (m là tham số thực) thoả mãn 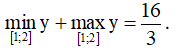. Mệnh đề nào dưới đây đúng ?

A. m = 1.                    B. m = 5.                C. m = 3.                   D. m = 2.

Câu 29. Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số 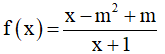 trên đoạn [0;1] bằng - 2?

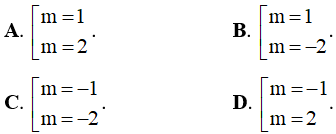
Câu 30. Cho hàm số 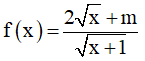 với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3  

A. m ∈ (1;3)             B. m ∈ (1;3√5 - 4)             C. m ∈ (1;√5)              D. m ∈ (1;3] 

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
B	C	D	A	D	D	D	D	D	A	C	B	C	C	A
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
D	B	A	C	B	A	D	D	D	C	D	C	B	D	C

 

Dạng 2. Ứng dụng GTLN, GTNN của hàm số vào bài toán thực tế.

1. Phương pháp giải:

Bước 1: Từ các điều kiện của bài toán xây dựng hàm số.

Bước 2: Tìm tập xác định của hàm số.

Bước 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số vừa xây dựng trên tập xác định của nó phù hợp với yêu cầu bài toán.

Bước 4:  Kết luận.

2. Ví dụ minh hoạ.

Ví dụ 1. Trong tất cả các hình chữ nhật có cùng diện tích   thì hình chữ nhật có chu vi nhỏ nhất bằng bao nhiêu?

A. 2√S .              B. 4√S.             C. 2S .                 D. 4S.

Lời giải

Gọi a,b > 0 lần lượt là chiều dài và chiều rộng của hình chữ nhật cần tìm.

Diện tích của hình chữ nhật: S = ab.

Chu vi hình chữ nhật: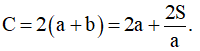  

Khảo sát hàm 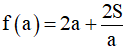 trên (0;+∞) , ta được min f(a) = 4√S khi a = √S.  

Chọn B.

Cách 2. Ta có P = 2(a+b) ≥ 2.2√ab = 4√ab = 4√S. Dấu ''='' xảy ra ⇔ a = b .

Ví dụ 2. Một mảnh vườn hình chữ nhật có diện tích 961cm², người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm của hình chữ nhật (xem hình minh họa). Tính diện tích nhỏ nhất S_min của 4 phần đất được mở rộng.

A. S_min = 961π - 961(m²)               C. S_min = 1892π - 946(m²) 

B. S_min = 1922π - 961(m²)             D. S_min = 480,5π - 961(m²) 

Lời giải

Gọi x(m), y(m) ( x > 0, y > 0) lần lượt là hai kích thước mảnh vườn hình chữ nhật; R(m) là bán kính hình tròn ngoại tiếp mảnh vườn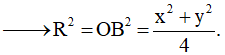 

Theo đề bài, ta có xy = 961m² .

Diện tích 4 phần đất mở rộng: S = S_tron - S_ABCD = πR² - xy 

 

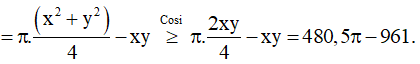
Chọn D.

Nhận xét. Dấu '' = '' xảy ra khi ABCD là hình vuông. Nếu phát hiện đều này thì làm trắc nghiệm rất nhanh.

3. Bài tập vận dụng. 

Câu 1. Trong tất cả các hình chữ nhật có cùng chu vi bằng 16cm thì hình chữ nhật có diện tích lớn nhất bằng:

A. 36cm².           B. 20cm².          C. 16cm².            D. 30cm². 

Câu 2. Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

A. x = 6 .             B. x = 3.            C. x = 2.              D. x = 4.

Câu 3. Tính diện tích lớn nhất S_max của hình chữ nhật nội tiếp trong nửa đường tròn có bán kính 10cm, biết một cạnh của hình chữ nhật nằm dọc theo đường kính của đường tròn.

A. S_max = 80cm²                             B. S_max = 100cm² 

C. S_max = 160cm²                            D. S_max = 200cm² 

Câu 4. Một ngọn hải đăng đặt ở vị trí A cách bờ biển một khoảng AB = 5km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7km. Người canh hải đăng có thể chèo đò từ A đến vị trí M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Vị trí của điểm M cách B một khoảng gần nhất với giá trị nào sau đây để người đó đến kho nhanh nhất?

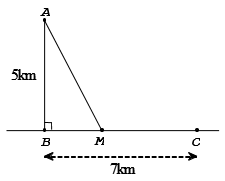
A. 3,0km                                                   B. 7,0km 

C. 4,5km                                                   D. 2,1km       

Câu 5. Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh a, đoạn dây thứ hai uốn thành đường tròn bán kính r. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì tỉ số  bằng:

 

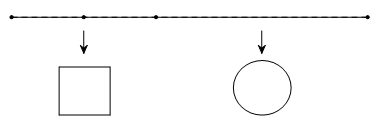
Câu 6. Một mảnh giấy hình chữ nhật có chiều dài 12cm và chiều rộng 6cm. Thực hiện thao tác gấp góc dưới bên phải sao cho đỉnh được gấp nằm trên cạnh chiều dài còn lại. Hỏi chiều dài L tối thiểu của nếp gấp là bao nhiêu?

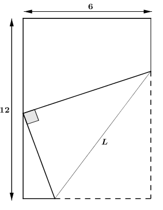
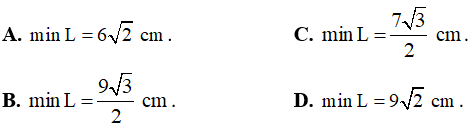
Đáp án

1	2	3	4	5	6
C	C	B	C	B	B

Phần 4: Các dạng bài tập về tiệm cận của đồ thị hàm số

A. LÝ THUYẾT.

1. Đường tiệm cận đứng.

Cho hàm số y = f(x) xác định trên một khoảng vô hạn (là khoảng dạng (a;+∞); (-∞;b) hoặc (-∞;+∞) ).

- Định nghĩa: Đường thẳng x = x₀ được gọi là đường tiệm cận đứng của đồ thị hàm số nếu ít nhất một trong các điều kiện sau đây được thỏa mãn:

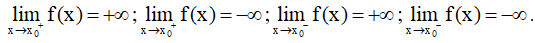
2. Đường tiệm cận ngang.

- Định nghĩa: Đường thẳng y = y₀ được gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn: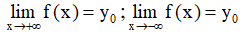 

Chú ý:

- Đồ thị hàm số 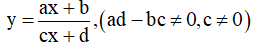 luôn có tiệm cận ngang và tiệm cận đứng lần lượt là  .

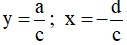- Nếu 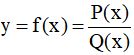 là hàm số phân thức hữu tỉ.

+ Nếu Q(x) = 0 có nghiệm là x₀, và x₀ không là nghiệm của P(x) = 0 thì đồ thị có tiệm cận đứng là x = x₀ .

+ Nếu bậc (P(x)) ≤ bậc (Q(x)) thì đồ thị hàm số có tiệm cận ngang.

B. CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Xác định tiệm cận của hàm số.

1. Phương pháp giải.

Dựa vào định nghĩa để giải bài toán.

2. Ví dụ minh hoạ.

Ví dụ 1. Tiệm cận đứng của đồ thị hàm số 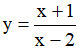 là đường thẳng có phương trình:

A. x = -1 .                    B. x = -2.              C. x = 2                     D. x = 1

Lời giải

Ta có: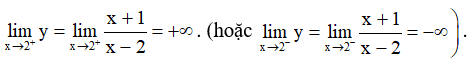 

Vậy x = 2 là tiệm cận đứng của đồ thị hàm số.

Chọn C.

 Ví dụ 2. Cho hàm số xác định và liên tục trên có bảng biến thiên như sau:

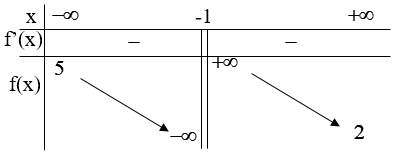
Khẳng định nào sau đây là khẳng định đúng? 

A. Đồ thị hàm số có một đường tiệm cận. 

B. Đồ thị hàm số có hai đường tiệm cận.

C. Đồ thị hàm số có hai TCN và một TCĐ  

D. Đồ thị hàm số có bốn đường tiệm cận.

Lời giải

Từ bảng biến thiên, ta có:

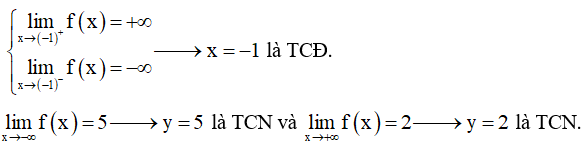
Chọn C.

Ví dụ 3. Chọn khẳng định đúng trong các khẳng định sau:

A. Đồ thị hàm số y = f(x) có tiệm cận ngang y = 1 khi và chỉ khi 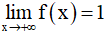 và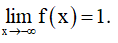 

B. Nếu hàm số y = f(x) không xác định tại x₀ thì đồ thị hàm số y = f(x) có tiệm cận đứng x = x₀ .

C. Đồ thị hàm số y = f(x) có tiệm cận đứng x = 2 khi và chỉ khi 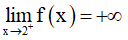 và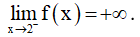 

D. Đồ thị hàm số y = f(x) bất kì có nhiều nhất hai đường tiệm cận ngang.

Lời giải

A sai vì chỉ cần một trong hai giới hạn 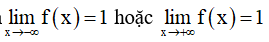 tồn tại thì đã suy ra được tiệm cận ngang là y = 1.

B sai, ví dụ hàm số 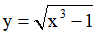 không xác định tại x = -2 nhưng  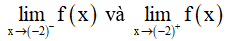không tiến đến vô cùng nên   không phải là tiệm cận đứng của đồ thị hàm số.

C sai vì chỉ cần tồn tại một trong bốn giới hạn sau:

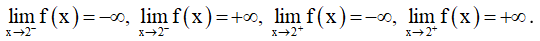
D đúng vì chỉ có hai giới hạn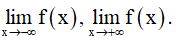 

Chọn D.

3. Bài tập vận dụng.

Câu 1. Tiệm cận đứng của đồ thị hàm số 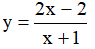 là

A. x = -2.                 B. x = 1                 C. x = -1                      D. x = 2 

Câu 2. Tiệm cận ngang của đồ thị hàm số 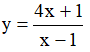 là

A. y = 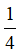. B. y = 4                C. y = 1                 D. y = -1

Câu 3. Tiệm cận ngang của đồ thị hàm số 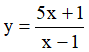 là:

A. y = 1.                 B. 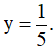            C. y = -1              D. y = 5

Câu 4. Cho hàm số 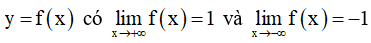. Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số không có tiệm cận ngang. 

B. Đồ thị hàm số có đúng một tiệm cận ngang.

C. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y = 1 và y = -1

D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng x = 1 và x = -1.

Câu 5. Cho hàm số 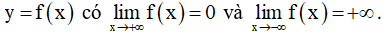. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số nằm phía trên trục hoành.

C. Đồ thị hàm số có một tiệm cận ngang là trục hoành.

D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng y = 0 

Câu 6. Cho hàm số 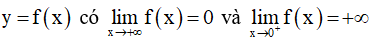. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận đứng.

B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho.

C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng  .

D. Hàm số đã cho có tập xác định là D = (0,+∞).

Câu 7. Cho hàm số y = f(x) xác định và liên tục trên R\{-1} , có bảng biến thiên như sau: 

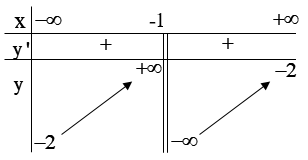
Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số có tiệm cận đứng y = -1 và tiệm cận ngang x = -2 

B. Đồ thị hàm số có duy nhất một tiệm cận.

C. Đồ thị hàm số có ba tiệm cận.

D. Đồ thị hàm số có tiệm cận đứng x = -1 và tiệm cận ngang y = -2  

Câu 8. Cho hàm số y = f(x) xác định và liên tục trên R\{-1} có bảng biến thiên như sau:

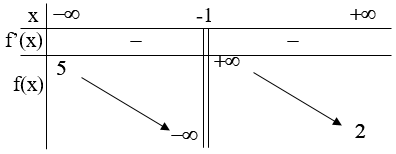
Khẳng định nào sau đây là khẳng định đúng? 

A. Đồ thị hàm số có một đường tiệm cận. 

B. Đồ thị hàm số có hai đường tiệm cận.

C. Đồ thị hàm số có hai TCN y = 2, y = 5 và một TCĐ x = -1 

D. Đồ thị hàm số có bốn đường tiệm cận.

Câu 9. Cho hàm số y = f(x) xác định trên R\, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: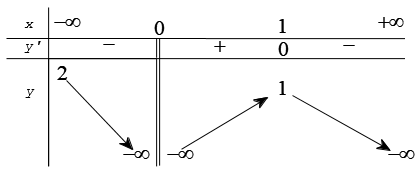

Mệnh đề nào sau đây là đúng?

A. Đồ thị hàm số có một đường tiệm cận đứng.

B. Hàm số đạt cực tiểu tại x = 0 

C. Giá trị lớn nhất của hàm số là 1 

D. Hàm số không có cực trị. 

Câu 10. Cho hàm số y = f(x) có bảng biến thiên như sau: 

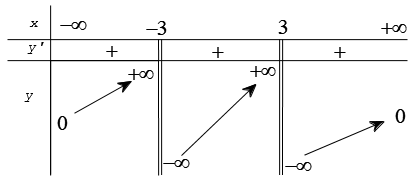
Mệnh đề nào sau đây là sai?

A. Đồ thị hàm số có tiệm cận đứng là x = -3 

B. Đồ thị hàm số có tiệm cận đứng là x = 3 

C. Đồ thị hàm số có tiệm cận ngang là y = 0 

D. Đồ thị hàm số có tất cả hai đường tiệm cận.

Câu 11. Cho hàm số y = f(x) có bảng biến thiên như sau:

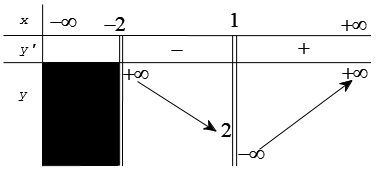
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?

A. 1                   B. 2                  C. 3                   D. 4

Câu 12. Tìm số tiệm cận đứng của đồ thị hàm số .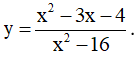

A. 2.                   B. 3.                   C. 0.                   D. 1.

Câu 13. Đồ thị hàm số nào trong các hàm số dưới đây có tiệm cận đứng?

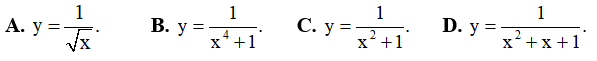
Câu 14. Đồ thị hàm số 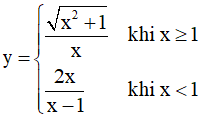 có tất cả bao nhiêu đường tiệm cận?

A. 1.                   B. 2.                   C. 3.                   D. 4.

Câu 15. Đồ thị hàm số nào sau đây có đúng hai tiệm cận ngang?

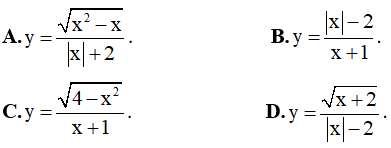
Câu 16. Đồ thị hàm số 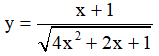 có tất cả bao nhiêu đường tiệm cận?

A. 1.                   B. 2.                 C. 3                   D. 4.

Câu 17. Đồ thị hàm số 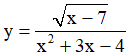 có bao nhiêu đường tiệm cận đứng?

A. 1.                   B. 2.                  C. 0.                    D. 3.

Câu 18. Gọi n,d lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số 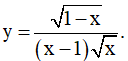 Khẳng định nào sau đây là đúng?

A. n = d = 1         B. n = 0; d = 1          C. n = 1; d = 2         D. n = 0; d = 2 

Câu 19. Đồ thị hàm số 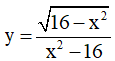 có tất cả bao nhiêu đường tiệm cận?

A. 0.                   B. 1.                  C. 2.                   D. 3.

Câu 20. Cho hàm số 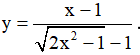. Gọi d,n lần lượt là số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số. Mệnh đề nào sau đây là đúng?

A. n + d = 1         B. n + d = 2          C. n + d = 3         D. n + d = 4

Câu 21. Tìm số tiệm cận đứng của đồ thị hàm số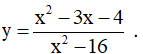 

A. 2.                      B. 3.                    C. 1.                          D. 0.

Câu 22. Cho đường cong 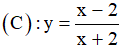. Điểm nào dưới đây là giao của hai tiệm cận của (C)?

A. L(-2,2).                 B. M(2,1).                  C. N(-2;-2).                  D. K(-2,1) .

Câu 23. Đồ thị của hàm số nào dưới đây không có tiệm cận đứng ?

Câu 24. Đồ thị của hàm số 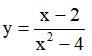 có bao nhiêu tiệm cận ?

A. 0                             B. 3                     C. 1                           D. 2

Câu 25. Tổng số các đường tiệm cận đứng và tiệm cận ngang của hai đồ thị hàm số 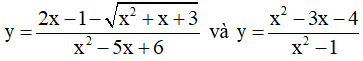 là

A. 5.                            B. 3.                     C. 2.                          D. 4.

Câu 26. Các đường tiệm cận của đồ thị hàm số 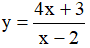 tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

A. 3.                             B. 12.                       C. 8.                         D. 6.

Câu 27. Cho hàm số 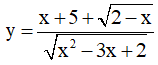. Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số có một đường tiệm cận ngang là đường thẳng y = 1 .

B. Đồ thị hàm số có một đường tiệm cận ngang là đường thẳng y = 0 .

C. Đồ thị hàm số có một đường tiệm cận ngang là đường thẳng y = -1.

D. Đồ thị hàm số có hai đường tiệm cận ngang là hai đường thẳng y = -1 và y = 1

Câu 28. Tìm điểm M thuộc đồ thị hàm số 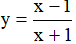 sao cho khoảng cách từ M  đến tiệm cận ngang bằng khoảng cách từ M  đến trục tung.

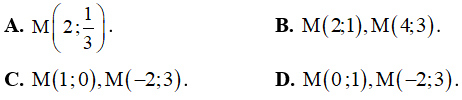
Câu 29. Cho hàm số 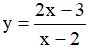(C). Gọi M là điểm bất kỳ trên (C), d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d là

A. 5                                     B. 10                     C. 6.                      D. 2 

Câu 30. Cho hàm số 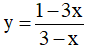 có đồ thị (C). Điểm M nằm trên (C) sao cho khoảng cách từ M đến tiệm cận đứng gấp hai lần khoảng cách từ M đến tiệm cận ngang của (C). Khoảng cách từ M đến giao điểm hai đường tiệm cận của (C) bằng

A. 3√2 .                                B. 4                      C. 5 .                      D. 2√5 .

Đáp án

 

                           

Dạng 2. Tìm m để hàm số có tiệm cận thoả mãn điều kiện cho trước.

1. Phương pháp giải.

Bước 1. Tìm điều kiện của tham số để hàm số xác định.

Bước 2. Tìm các đường tiệm cận của đồ thị hàm số.

Bước 3. Giải điều kiện của bài toán để tìm tham số.

Bước 4. Kết luận

Lưu ý: Với Hàm số 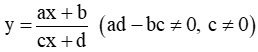, ta có:

Gọi M(x₀,y₀) là điểm thuộc đồ thị hàm số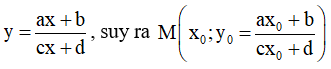 

Đồ thị hàm số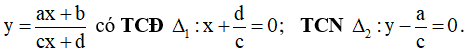 

Ta có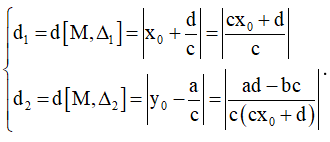 

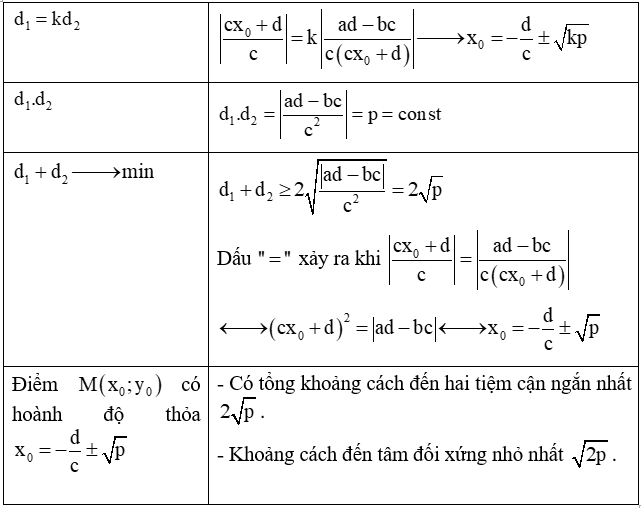
2. Ví dụ minh hoạ.

Ví dụ 1. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 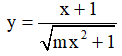 có hai tiệm cận ngang.

A. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.    

B. m < 0 .                                      

C. m = 0           

D. m > 0

Lời giải

Khi m > 0 ta có:

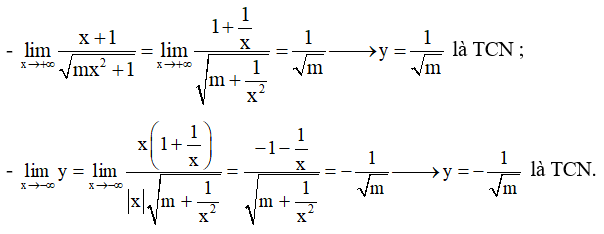
Với m = 0 suy 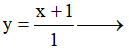 đồ thị hàm số không có tiệm cận.

Với m < 0 thì hàm số có TXĐ là một đoạn nên đồ thị hàm số không có TCN.

Vậy với m > 0 thì đồ thị hàm số có hai tiệm cận ngang. 

Chọn D.

Ví dụ 2. Tìm trên đồ thị hàm số 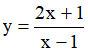 những điểm M sao cho khoảng cách từ M đến tiệm cận đứng bằng ba lần khoảng cách từ M đến tiệm cận ngang của đồ thị.

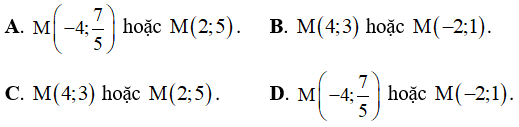
Lời giải

Gọi 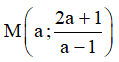 với a ≠ 0 là điểm thuộc đồ thị.

Đường tiệm cận đứng d: x = 1 đường tiệm cận ngang d': y = 2 .

Yêu cầu bài toán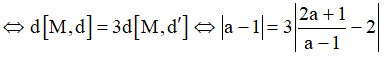  

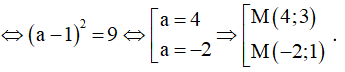
Chọn B.

Áp dụng công thức giải nhanh.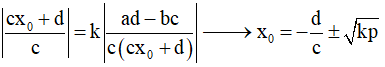  

với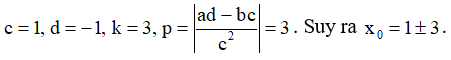 

3. Bài tập tự luyện.

Câu 1. Tìm tất cả các giá trị thực của tham số m để đường tiệm cận ngang của đồ thị hàm số 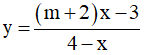 đi qua điểm A(-1;2) .

A. m = -2                    B. m = 1                 C. m = -4               D. m = 2   

Câu 2. Tìm tất cả các giá trị thực của tham số m để đường tiệm cận đứng của đồ thị hàm số 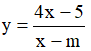 đi qua điểm A(-3;1) .

A. m = -3                   B. m = -4            C. m = 5               D. m = 4

Câu 3. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2021;2021] để đồ thị hàm số 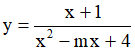 có 3 đường tiệm cận?

A. 4033.                   B.  4034                C. 2017                D.  2016

Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 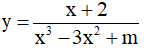 có nhiều đường tiệm cận nhất.

Câu 5. Số các giá trị của tham số m để đồ thị hàm số 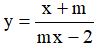 có đúng 1 tiệm cận đứng và 1 tiệm cận ngang, đồng thời hai tiệm cận này tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 18 là

A. 0.                          B. 1.                       C. 2.                      D. 3.

Câu 6. Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hàm số 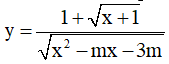 có đúng hai tiệm cận đứng.

Câu 7. Có bao nhiêu giá trị thực của m để đồ thị hàm số 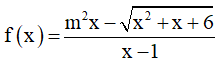 có tiệm cận ngang là đường thẳng  .

A. 1 .                    B. 2 .                      C. 4 .                      D. Vô số.

Câu 8. Đồ thị của hàm số 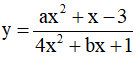 có một đường tiệm cận ngang là y = c và chỉ có một đường tiệm cận đứng. Tính  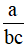biết rằng a là số thực dương và ab = 4 ?

Câu 9. Có bao nhiêu giá trị nguyên của tham số a ∈  [-2021;2021] để đồ thị hàm số 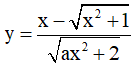 có tiệm cận ngang?

A. 2022.                  B. 2021.                 C. 4042.                 D. 2020.

Câu 10. Cho hàm số 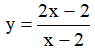 có đồ thị là (C), M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn AB = 2√5. Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Tìm giá trị của S .

A. 8 .                       B. 9 .                      C. 5 .                      D. 6 .

Câu 11. Nếu đồ thị 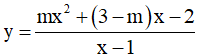 có đường tiệm cận xiên tiếp xúc với đường tròn có phương trình (x - 1)² + (y - 4)² = 2 thì tập tất cả các giá trị của m là:

A. -1 .                  B. 2.                    C. 1.                   D. 3.

Câu 12. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 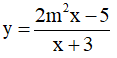 nhận đường thẳng y = 8 làm tiệm cận ngang.

A. m = 2            B. m = -2           C. m = ±2             D. m = 0

Câu 13. Biết rằng đồ thị hàm số 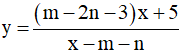 nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng S = m² + n² - 2 

A. S = 2              B. S = 0              C. S = 1             D. S = -1

Câu 14. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 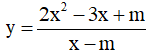 không có tiệm cận đứng.

A. m = 0 .                                       B. m = 1,m = 2.   

C. m = 0,m = 1                               D. m = 1

Câu 15. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 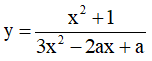 có đúng một tiệm cận đứng.

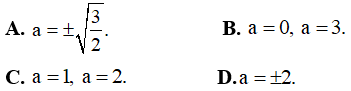
Câu 16. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 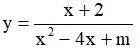 có đúng một tiệm cận ngang và đúng một tiệm cận đứng.

A. m < 4            B. m > 4           C. m = 4, m = -12            D. m ≠4 

Câu 17. Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-2017;2017] để hàm số 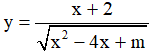 có hai tiệm cận đứng.

A. 2018             B. 2019           C. 2020              D. 2021

Câu 18. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 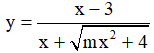 có đúng một tiệm cận ngang.

A. m = 0,m = 1        B. m ≥ 0           C. m = 1             D. m = 0 

Câu 19. Cho hàm số 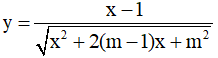 với m là tham số thực và  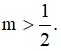Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?

A. 1.                   B. 2.                 C. 3.                   D. 4.

Câu 20. Cho hàm số 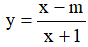(C) với m là tham số thực. Gọi M là điểm thuộc (C) sao cho tổng khoảng cách từ M đến hai đường tiệm cận của (C) nhỏ nhất. Tìm tất cả các giá trị của m để giá trị nhỏ nhất đó bằng 2

A. m = 0             B. m = 2           C. m = 0,m = -2         D. m = 1

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
C	A	A	C	C	A	C	B	A	A	A	C	B	C	B	C	C	A	B	C

Phần 5: Các dạng bài tập nhận dạng đồ thị hàm số

A. LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI

1.Nhận dạng đồ thị hàm số bậc 3: y = ax³ + bx² + cx + d 

	a > 0	a < 0
y' = 0 có hai nghiệm phân biệt hay  Δy > 0
y' = 0 có nghiệm kép hay Δy = 0
y' = 0 vô nghiệm hay Δy < 0

 

Hệ số a	Đồ thị hướng lên	a > 0
	Đồ thị hướng xuống	a < 0
Hệ số b	Điểm uốn "lệch phải" so với Oy hoặc 2 điểm cực trị lệch phải so với Oy	ab < 0
	Điểm uốn "lệch trái" so với Oy hoặc hai điểm cực trị "lệch trái" so với Oy	ab > 0
	Điểm uốn thuộc Oy hoặc hai điểm cực trị cách đều trục Oy	b = 0
Hệ số c	Không có cực trị	c = 0  hoặc ac > 0
	Hai điểm cực trị nằm về hai phía trục tung Oy	ac < 0
	Có 1 điểm cực trị nằm trên Oy	c = 0
Hệ số d	Giao điểm với trục tung nằm trên điểm O	d > 0
	Giao điểm với trục tung nằm dưới điểm O	d < 0
	Giao điểm với trục tung trùng điểm O	d = 0

2. Nhận dạng đồ thị hàm bậc 4 trùng phương: y = ax⁴ + bx² + c

+) Đạo hàm: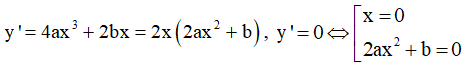 

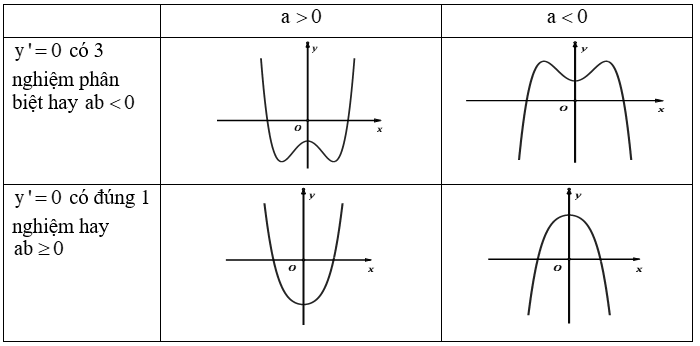
Hệ số a	Đồ thị có bề lõm hướng lên	a > 0
	Đồ thị có bề lõm hướng xuống	a < 0
Hệ số b	Đồ thị hàm số có 3 điểm cực trị	ab < 0
	Đồ thị hàm số chỉ có 1 điểm cực trị (Đang xét a ≠ 0)	ab ≥ 0
Hệ số c	Giao điểm với trục tung nằm trên điểm O	c > 0
	Giao điểm với trục tung nằm dưới điểm O	c < 0
	Giao điểm với trục tung trùng điểm O	c=0

3. Nhận dạng đồ thị hàm số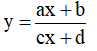 

+ Tập xác định: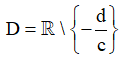  

+ Đạo hàm: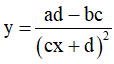  

+ Đồ thị hàm số có: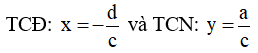 

+ Đồ thị có tâm đối xứng: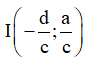  

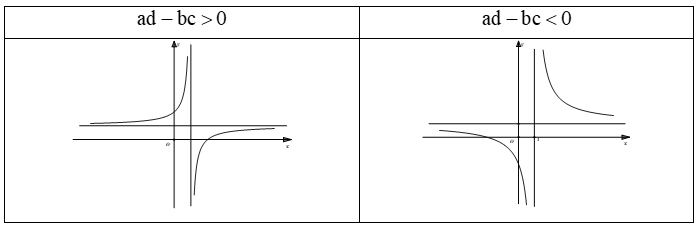
Tiêu chí nhận dạng:

- Dựa vào tiệm cận đứng + tiệm cận ngang.

- Dựa vào giao Ox,Oy

- Dựa vào sự đồng biến, nghịch biến.

ab	Giao Ox nằm phía "phải" điểm O	ab < 0
	Giao Ox nằm phía "trái" điểm O	ab > 0
	Không cắt Ox	a = 0
ac	Tiệm cận ngang nằm "phía trên" Ox	ac > 0
	Tiệm cận ngang nằm "phía dưới" Ox	ac < 0
	Tiệm cận ngang trùng Ox	a = 0
bd	Giao Oy nằm trên điểm O	bd > 0
	Giao Oy nằm dưới điểm O	bd < 0
	Giao Oy trùng gốc tọa độ O	b = 0
cd	Tiệm cận đứng nằm "bên phải" Oy	cd < 0
	Tiệm cận đứng nằm "bên trái" Oy	cd > 0
	Tiệm cận đứng trùng Oy	d = 0

4. Lưu ý:

- Tại giao điểm với trục Ox thì thay y = 0 và biện luận.

- Tại giao điểm với trục Oy thì thay x = 0 và biện luận.

B. VÍ DỤ MINH HOẠ.

Ví dụ 1. Cho hàm số f(x) = ax³ + bx² + cx + d (a,b,c,d ∈ R) có bảng biến thiên như sau:

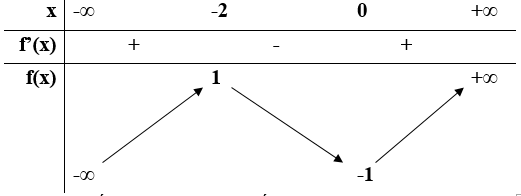
Có bao nhiêu số dương trong các số a,b,c,d 

A. 3                       B. 4                       C. 2                       D. 1 

Lời giải

Chọn C

 

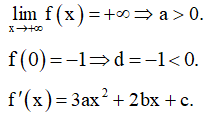
Ta có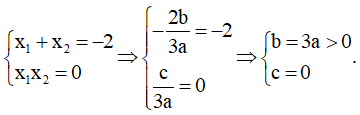  

Vậy có 2 giá trị dương là a và b.

Ví dụ 2. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

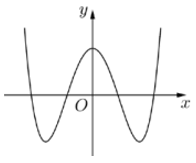
A. y = x³ - 3x + 1                                                       B. y = -2x⁴ + 4x² + 1  

C. y = -x³ + 3x + 1                                                     D. y = 2x⁴ - 4x² + 1

Lời giải

Từ đồ thị ta thấy:

- Đây là đồ thị hàm bậc 4 trùng phương

- Đồ thị hàm số có dạng hình chữ w nên a > 0 

Chọn D.

Ví dụ 3. Cho hàm số 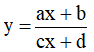 có bảng biến thiên như hình vẽ bên. Hỏi hàm số đã cho là hàm số nào?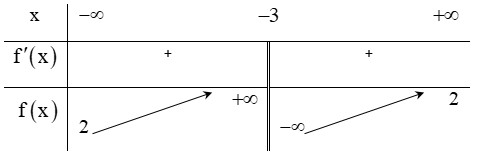

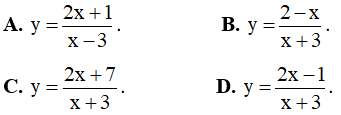
Lời giải

Dựa vào bảng biến thiên ta thấy:

+ Đồ thị hàm số nhận đường thẳng x = -3 là tiệm cận đứng và đường thẳng y = 2 là tiệm cận ngang (loại đáp án A và B).

+ Hàm số đã cho đồng biến trên mỗi khoảng xác định. 

Xét hàm số 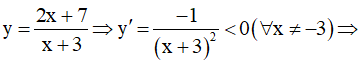 Hàm số nghịch biến trên mỗi khoảng xác định nên ta loại đáp án C. 

Chọn D.

                                 

C. BÀI TẬP TỰ LUYỆN.

Câu 1. Đồ thị của hàm số dưới đây có dạng như đường cong bên?

A. y = x³ - 3x + 1                                                          B. y = x⁴ - 2x² + 1  

C. y = -x⁴ + 2x² + 1                                                      D. y = -x³ + 3x + 1

Câu 2. Đồ thị hình bên là của hàm số nào?

A. y = -x² + x - 1 .                         B. y = -x³ + 3x + 1

C. y = x⁴ - x² + 1                           D. y = x³ - 3x + 1

Câu 3. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?

 

A. y = x³ - 3x + 2                                            B. y = x⁴ - x² + 1      

C. y = x⁴ + x² + 1                                            D. y = -x³ + 3x + 2

Câu 4. Đồ thị sau đây là của hàm số nào?

 

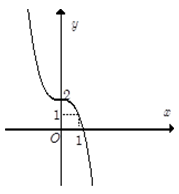
A. y = -x³ + 1                             B. y = -x³ + 3x + 2

C. y = -x³ - x + 2                        D. y = -x³ + 2

Câu 5. Cho hàm số y = f(x) có bảng biến thiên sau:

 

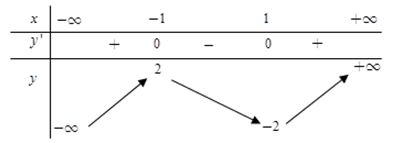
Đồ thị nào sau đây thể hiện hàm số y = f(x)?

                          

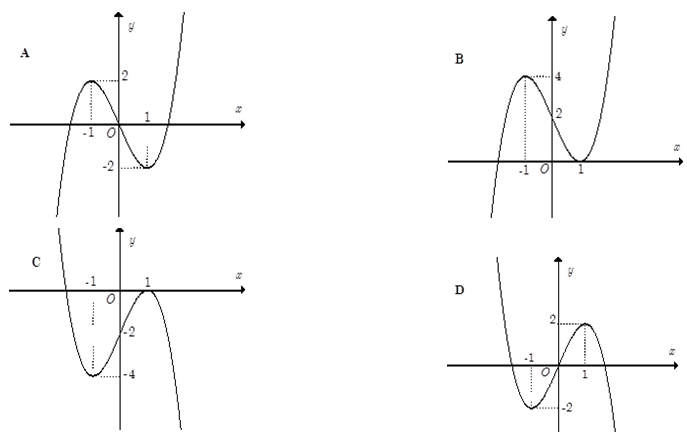
Câu 6. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ?

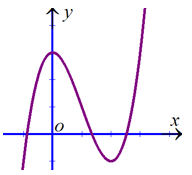
A. y = 2x + 5.                                           B. x = 2.

C. x = -5.                                                 D. y = x³ - 3x² + 3

Câu 7. Cho hàm số y = ax³ + bx² + cx + d có đồ thị như hình bên. Chọn đáp án đúng?

 

A. Hàm số có hệ số a < 0 .

B. Hàm số đồng biến trên các khoảng (-2;-1) và (1;2).

C. Hàm số không có cực trị.

D. Hệ số tự do của hàm số khác 0.

Câu 8. Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ? 

 

A. y = -x³ + 3x -1                                  B. y = x⁴ - x² - 1

C. y = x³ - 3x -1                                    D. y = -x⁴ + x² - 1

Câu 9. Đồ thị sau đây là của hàm số nào?

 

A. y = x⁴ - 2x² - 1                       B. y = -2x⁴ + 4x² - 1

C. y = -x⁴ + 2x² - 1                     D. y = -x⁴ - x² - 1

Câu 10. Đồ thị hình bên là của hàm số nào?

 

A. y = -x⁴ - 2x² + 3                     B. y = -x⁴ - 2x² - 3

C. y = -x⁴ + 2x² + 3                    D. y = x⁴ + 2x² + 3

Câu 11. Đồ thị sau đây là của hàm số nào?

 

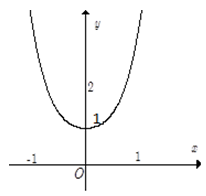
A. y = x⁴ + x² + 2                         B. y = x⁴ - x² + 2

C. y = x⁴ - x² + 1                          D. y = x⁴ + x² + 1

Câu 12. Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số y = |2x² - x⁴ + 1| ?

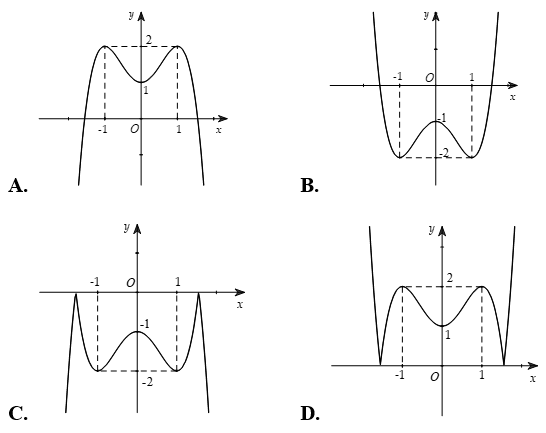
Câu 13. Đồ thị sau đây là của hàm số nào?

 

 

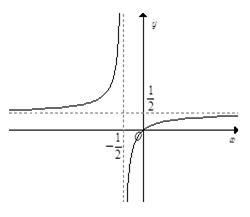
Câu 14. Đường cong ở hình bên là đồ thị của hàm số 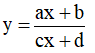 với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng ?

 

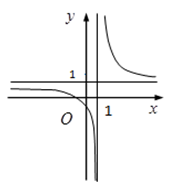
A. y' > 0,∀x ∈ R                                                                B. y' < 0,∀x ∈ R

C. y' > 0,∀x ≠ 1                                                                 D. y' < 0,∀x ≠ 1

Câu 15. Cho hàm số y = x³ - 6x² + 9x có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?

A. y = -x³ + 6x² - 9x                       B. y = |x|³ + 6|x|² + 9|x| 

C. y = |x³ - 6x² + 9x|                      D. y = |x|³ - 6x² + 9|x| 

Câu 16. Cho hàm số y = x³ + 3x² - 2  có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?

A. y = |x|³ + 3|x|² - 2               B. y = |x³ + 3x² - 2|

C. y = ||x|³ + 3x² - 2|               D. y = -x³ - 3x² + 2

Câu 17. Cho hàm số 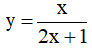 có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?

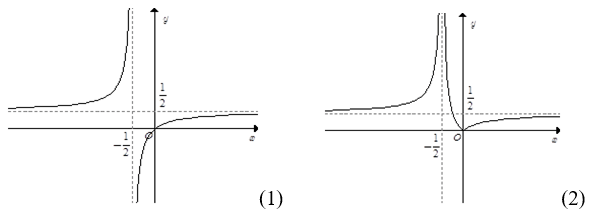
Câu 18. Cho hàm số 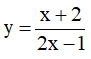 có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?

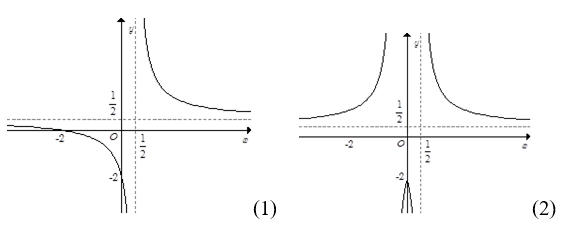
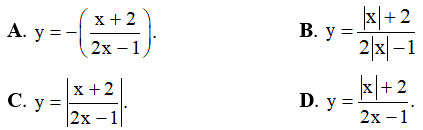
Câu 19. Cho hàm số y = x³ + bx² + cx + d 

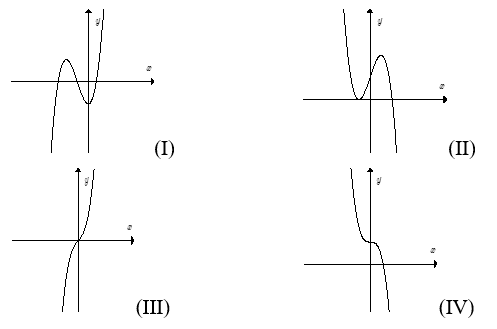
Các đồ thị nào có thể là đồ thị biểu diễn hàm số đã cho?

A. (I).               B. (I) và (III).             C. (II) và (IV).               D. (III) và (IV).

Câu 20. Cho hàm số y = x³ + bx² - x + d

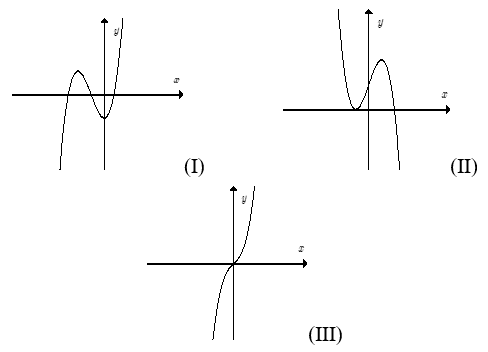
Các đồ thị nào có thể là đồ thị biểu diễn hàm số đã cho?

A. (I).                 B. (I) và (II).       

C. (III).               D. (I) và (IIII)

Câu 21. Cho hàm số y = f(x) = x³ + bx² + cx + d

Trong các mệnh đề sau hãy chọn mệnh đề đúng:

A. Đồ thị (I) xảy ra khi a < 0 và f'(x) = 0 có hai nghiệm phân biệt.

B. Đồ thị (II) xảy ra khi a ≠ 0 và f'(x) = 0 có hai nghiệm phân biệt.

C. Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm hoặc có nghiệm kép.

D. Đồ thị (IV) xảy ra khi a > 0 và f'(x) = 0 có nghiệm kép.

Câu 22. Cho hàm số y = f(x) có bảng biến thiên như sau:

 

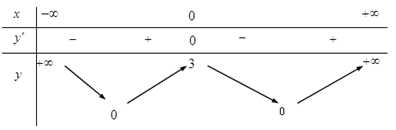
Mệnh đề nào dưới đây là sai ?

A. Hàm số có ba điểm cực trị.                   B. Hàm số có giá trị cực đại bằng 3.

C. Hàm số có giá trị cực đại bằng 0.         D. Hàm số có hai điểm cực tiểu.

Câu 23. Cho hàm số y = f(x) có bảng biến thiên như sau. Tìm giá trị cực đại y_CĐ và giá trị cực tiểu y_CT của hàm số đã cho.

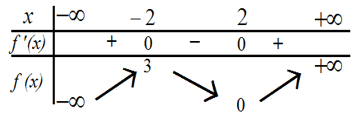
A. y_CĐ = 3 và y_CT = -2                                 B. y_CĐ = 2 và y_CT = 0 . 

C. y_CĐ = -2  và y_CT = 2  .                             D. y_CĐ = 3 và y_CT = 0 .

Câu 24. Cho hàm số y = f(x). Đồ thị của hàm số y= f’(x) như hình bên. Đặt h(x) = 2f(x) – x². Mệnh đề nào dưới đây đúng?

 

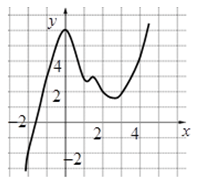
A. h(4) = h(-2) > h(2)                                                  B. h(4) = h(-2) < h(2) 

C. h(2) > h(4) > h(-2)                                                  D. h(2) > h(-2) > h(4)

Câu 25. Cho hàm số y = f(x). Đồ thị của hàm số y = f’(x) như hình bên. Đặt g(x) = 2f²(x) + x². Mệnh đề nào dưới đây đúng ? 

 

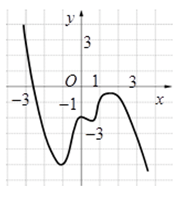
A. g(3) < g(-3) < g(1)                                B. g(1) < g(3) < g(-3) 

C. g(1) < g(-3) < g(3)                                D. g(-3) < g(3) < g(1)  

Câu 26. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

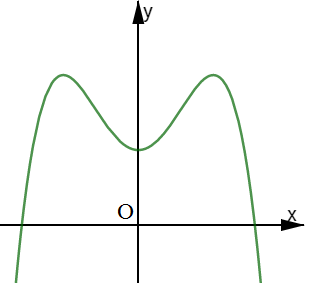
A. y = x³ - 3x² + 1 .                                              B. y = -x³ + 3x² + 1       

C. y = -x⁴ + 2x² + 1                                              D. y = x⁴ - 2x² + 1

Câu 27.  Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. y = x⁴ - 2x² + 1                                            B. y = -x⁴ + 3x² + 1     

C. y = x⁴ - 3x² + 1                                            D. y = -x⁴ - 2x² + 1

Câu 28. Cho hàm số y = ax³ + bx² + cx + d (a,b,c,d ∈ R) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a,b,c,d ?

A. 4                      B. 2.                      C. 1.                       D. 3.

Đáp án

Phần 6: Biện luận số nghiệm của phương trình dựa vào đồ thị hàm số

A. PHƯƠNG PHÁP GIẢI.

Đưa phương trình g(x;m) = 0 về các dạng bài sau:

Dạng 1: f(x) = h(m), trong đó h(m) là một hàm phụ thuộc vào tham số m.

- Vẽ đồ thị hàm số y = f(x), tìm các giá trị cực đại, cực tiểu, giá trị của hàm số tại các điểm đầu mút của miền xác định của hàm số y = f(x).

- Đường thẳng y = h(m) di động song song với trục hoành, dựa vào số giao điểm của đường thẳng y = h(m) với đồ thị hàm số y = f(x) để biện luận số nghiệm của phương trình g(x;m) = 0.

Dạng 2: f(x) = ax + b, trong đó a cố định, b thay đổi.

- Vẽ đồ thị hàm số y = f(x). 

- Tìm các tiếp tuyến với đồ thị hàm số y = f(x) có hệ số góc cho trước là a.

- Tìm giao điểm của tiếp tuyến với trục tung ( hoặc trục hoành) và giao điểm của đường thẳng y = ax + b với trục tung ( hoặc trục hoành). Cho b di động trên trục tung để suy ra số nghiệm của phương trình g(x;m).

Dạng 3: f(x) = ax + b, trong đó a thay đổi, b tùy ý.

- Vẽ đồ thị hàm số y = f(x).

- Tìm điểm A(x₀,y₀) là điểm cố định của đường thẳng y = ax + b

- Viết các phương trình tiếp tuyến với đồ thị hàm số y = f(x) đi qua A.

- Cho đường thẳng y = ax + b xoay quanh điểm cố định A. Từ đó suy ra nghiệm của phương trình g(x;m) = 0.

Chú ý:

- Nếu hàm số y = f(x) có miền xác định là đoạn thẳng [a,b] thì đồ thị hàm số y =f(x) ta chỉ xét phần x ∈ [a,b].

- Một số bài toán đặt ẩn phụ t = ∂(x), với ∂(x) là một biểu thức trong phương trình ban đầu thì:

+ Dựa vào miền xác định của x để tìm miền xác định của t.

+ Vẽ đồ thị hàm số y = f(t) rồi làm giống như trên.

- Đồ thị hàm số chứa giá trị tuyệt đối.

1. Dạng y = |f(x)|.

+ Vẽ đồ thị ( C) của hàm số y = f(x).

+ Lấy các phần của ( C) ở phía trên trục hoành.

+ Lấy thêm phần đối xứng qua trục hoành của các phần của ( C) phía dưới trục hoành.

2. Dạng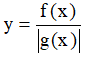  

+ Vẽ đồ thị ( C) của hàm số y = f(x).

+ Lấy các phần của ( C) tương ứng với x sao cho g(x) >0.

+ Lấy thêm phần đối xứng qua trục hoành của các phần của ( C) tương ứng với x sao cho g(x) <0.

3. Dạng 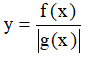 làm tương tự như mục 2.

4. Dạng y = f(x) + |g(x)|.

Đồ thị gồm 2 phần:

+ Đồ thị ( C) y= f(x) + g(x) tương ứng với x sao cho g(x) >0.

+ Đồ thị ( C’) y = f(x) – g(x) tương ứng với x sao cho g(x) <0.

5. Dạng y = f(|x|).

+ Vẽ đồ thị ( C) của hàm số y= f(x).

+ Lấy phần của ( C) bên phải trục oy tương ứng với x > 0.

+ Lấy thêm phần đối xứng qua trục oy của phần của ( C) bên phải trục oy.

Mở rộng: Đối với bài toán bất phương trình làm tương tự, lưu ý:

Giả sử hàm f(x) tồn tại Max-Min trên R. Ta có:

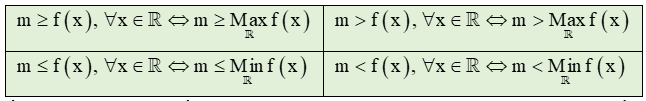
- Nếu hàm f(x) không tồn tại Max-Min trên R, tuy nhiên thông qua bảng biến thiên ta tìm được điều kiện bị chặn:M₁ < f(x) < M₂, khi đó:

Mở rộng: Đối với dạng bài tập phương trình tương giao.

- Cách giải: Chuyển tất cả ẩn, tham số của phương trình về 1 vế, ta sẽ được phương trình mới có dạng: g(x;m) = 0.

Như vậy, bài toán đã được đưa về dạng cơ bản. Tuỳ từng phương trình, chọn cách giải thích hợp.

B. Ví dụ minh hoạ.

Ví dụ 1. Cho hàm số y = 2x³ - 3x² + 1 có đồ thị (C). Biện luận theo m số nghiệm phương trình 2x³ - 3x² - m - 1 = 0 (*)

Lời giải

 

Đồ thị (C)

Ta có: 2x³ - 3x² - m - 1 = 0 ⇔ 2x³ - 3x² + 1 = m + 2 

Vậy số nghiệm của phương trình (*) bằng số điểm chung giữa đồ thị (C) và đường thẳng d: y = m + 2 .

- Với m + 2 < 0 hoặc m + 2 > 1 ⇔ m < -2 hoặc m > -1  thì d và (C) có một điểm chung => phương trình (*) có một nghiệm.

- Với m + 2 = 0 hoặc m + 2 = 1 ⇔ m = –2 hoặc m = –1 thì d và (C) có hai điểm chung => phương trình (*) có hai nghiệm.

- Với 0 < m + 2 < 1 ⇔ -2 < m < -1 thì d và (C) có ba điểm chung => phương trình (*) có ba nghiệm.

Ví dụ 2.  Cho hàm số y = x⁴ - 4x² + 3 có đồ thị (C). Tìm m để phương trình -x⁴ + 4x² - 3 - m = 0 (*) có 4 nghiệm phân biệt.

Lời giải

 

Đồ thị (C)

Ta có: (*) x⁴ - 4x² + 3 = m  

Số nghiệm của phương trình (*) bằng số điểm chung giữa đồ thị (C) và đường thẳng d: y = -m .

Vậy để phương trình (*) có 4 nghiệm phân biệt thì d và (C) phải cắt nhau tại 4 điểm.

=> -1 < -m < 3 ⇔ -3 < m < 1 

Vậy với -3 < m < 1 thì phương trình (*) có 4 nghiệm phân biệt.

Ví dụ 3. Cho hàm số y = f(x) = x⁴ - 2x² + 2 có bảng biến thiên như sau

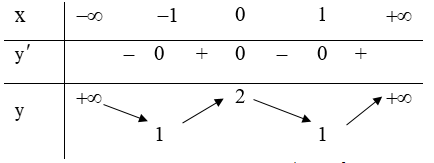
Số giá trị nguyên dương của m để phương trình 2x⁴ - 4x² + m - 5 = 0 có đúng 2 nghiệm

A. 3                          B. 4                        C. 5                        D. 6

Lời giải

Ta có: PT đã cho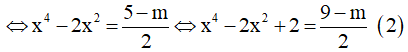  

Số nghiệm của phương trình (2) là số giao điểm của đồ thị (C) và đường thẳng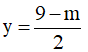  

Do vậy phương trình đã cho có 2 nghiệm ⇔ d cắt (C) tại 2 điểm phân biệt

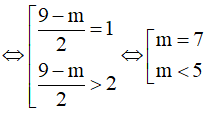
Kết hợp m ∈ Z⁺ => m = . 

Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán. 

Chọn C.

                               

C. BÀI TẬP VẬN DỤNG.

Câu 1. (Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình 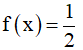 là

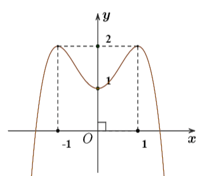
A. 2.                      B. 4.                           C. 3.                          D. 1.

Câu 2. Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình f(x) = 1 là:

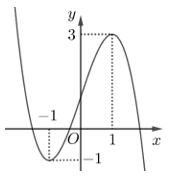
A. 0.                       B. 3.                       C. 1.                       D. 2.

Câu 3. Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ bên.

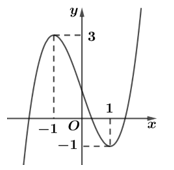
Số nghiệm thực của phương trình f(x) = 2 là:

A. 0 .                      B. 3                      C. 1                      D. 2 .

Câu 4. Cho hàm số y = f(x) xác định trên R\, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau.

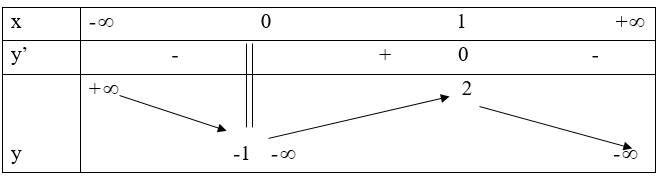
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm phân biệt.

A. [-1;2].                      B. (-1;2).                  C. (-1;2].                  D. (-  ;2].

Câu 5. Cho hàm số f(x) có bảng biến thiên như sau:

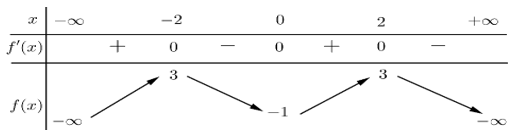
Số nghiệm thực của phương trình 2f(x) - 3 = 0 là:

A. 2.                          B. 1.                         C. 4.                         D. 3.

Câu 6. Cho hàm số f(x) có bảng biến thiên như sau:

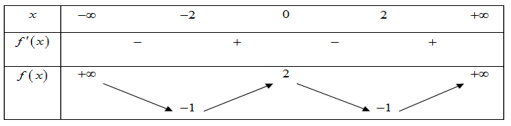
Số nghiệm thực của phương trình 3f(x) - 5 = 0 là:

A. 2                              B. 3                          C. 4                          D. 0

Câu 7. Cho hàm số y = -x⁴ + 2x² có đồ thị như hình bên. 

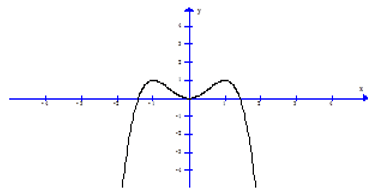
Tìm tất cả các giá trị thực của tham số m để phương trình -x⁴ + 2x² = m có bốn nghiệm thực phân biệt.

A. m > 0.                      B. 0 ≤ m ≤ 1.             C. 0 < m < 1 .             D. m<1.

Câu 8. Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. 

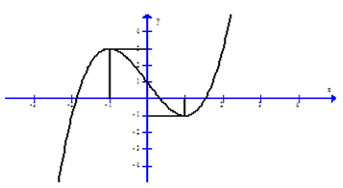
Tìm tất cả các giá trị m để phương trình f(sinx) = 0 có nghiệm thực thuộc khoảng (0;π).

A. [-1;3).               B. (-1; 1).              C. (-1;3).               D. [-1;1).

Câu 9. Cho hàm số f(x), hàm số y = f'(x) liên tục trên R và có đồ thị như hình vẽ bên.

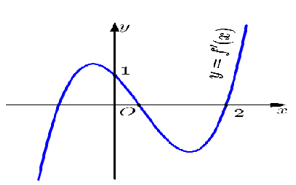
Bất phương trình f(x) < x + m ( m là tham số thực) nghiệm đúng với mọi x ∈ (0,2) khi và chỉ khi:

A. m ≥ f(2) - 2 .           B. m ≥ f(0)                C. m > f(2) - 2              D. m > f(0)

Câu 10. Cho hàm số f(x) , hàm số y = f’(x) liên tục trên R và có đồ thị như hình vẽ bên. 

 

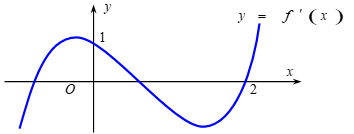
Bất phương trình f(x) > x + m (m là tham số thực) nghiệm đúng với mọi x ∈ (0,2) khi và chỉ khi:

A. m ≤ f(2) - 2                                 B. m < f(2) - 2              

C. m ≤ f(0)                                      D. m < f(0)       

Câu 11. Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

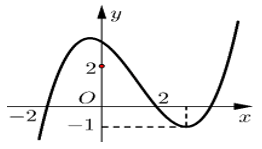
Số nghiệm thực của phương trình 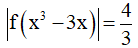 là

A. 3 .                    B. 8.                      C. 7 .                        D. 4.

Câu 12. Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

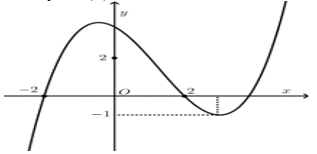
Số nghiệm thực của phương trình 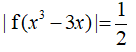 là:

A. 6.                    B. 10.                    C. 12                     D. 3.

Câu 13. Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như hình vẽ sau

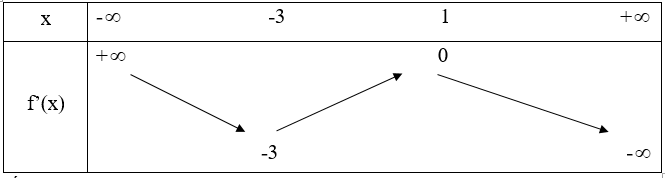
Bất phương trình f(x) < e^x + m đúng với mọi x ∈ (-1,1) khi và chỉ khi

Câu 14 Cho hàm số f(x) = mx⁴ + nx³ + px³ + px + r (m,n,q,p,r ∈ R) . 

Hàm số f’(x) có đồ thị như hình vẽ. 

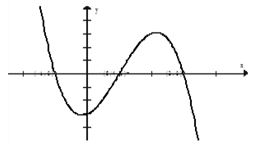
Tập nghiệm của phương trình f(x) = r có số phần tử là:

A. 4.                     B. 3.                       C. 1.                        D. 2.

Câu 15. Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình vẽ bên.

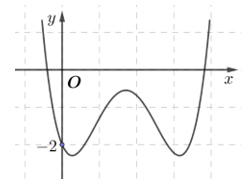
Số nghiệm thực phân biệt của phương trình f(x²f(x)) + 2 = 0 là

A. 8.                       B. 12 .                     C. 6 .                      D. 9 .

Câu 16. Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ bên.

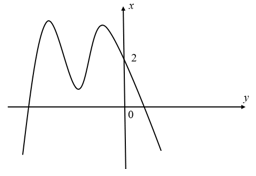
Số nghiệm thực của phương trình f(x²f(x)) = 2 là:

A. 6.                      B. 12.                     C. 8.                       D. 9.

Đáp án

 

Phần 7: Các dạng bài tập về sự tương giao của đồ thị hàm số

A. LÝ THUYẾT.

Cho hàm số y = f (x) có đồ thị (C₁) và y = g (x) có đồ thị (C₂) .

Phương trình hoành độ giao điểm của (C₁) và (C₂) là f (x) = g (x).

Khi đó:

- Số giao điểm của (C₁) và (C₂) bằng với số nghiệm của phương trình (1) .

- Nghiệm x₀ của phương trình (1) chính là hoành độ x₀ của giao điểm.

- Để tính tung độ y₀ của giao điểm, ta thay hoành độ x₀ vào y = f (x).

- Điểm M (x₀ ; y₀) là giao điểm của (C₁) và (C₂).

B. CÁC DẠNG TOÁN HAY GẶP VÀ CÁC KỸ NĂNG CẦN THIẾT.

Dạng 1. Tìm toạ độ giao điểm của các đồ thị hàm số cho trước.

1. Phương pháp giải.

Cho 2 hàm số y = f(x), y = g(x) có đồ thị lần lượt là (C) và (C’). 

Bước 1: Lập phương trình hoành độ giao điểm của (C) và (C’): f(x) = g(x)  

Bước 2: Giải phương trình tìm x từ đó suy ra y và toạ độ giao điểm.

Bước 3: Số nghiệm của (*) là số giao điểm của (C) và (C’). Thay trở lại y = f(x) (y = g(x)), ta sẽ được toạ độ giao điểm.

2. Ví dụ minh hoạ.

Ví dụ 1. Biết rằng đường thẳng y = -2x + 2 cắt đồ thị hàm số y = x³ + x + 2 tại điểm duy nhất có toạ độ (x₀,y₀). Tìm y₀.

 A. y₀ = 4.           B. y₀ = 0.           C. y₀ = 2           D. y₀ = -1

Lời giải

Phương trình hoành độ giao điểm: -2x + 2 = x³ + x + 2

⇔ x³ + 3x = 0 ⇔ x = 0 → y = 2  

Chọn C.

Ví dụ 2. Biết rằng đồ thị hàm số 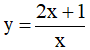 và đồ thị hàm số y = x² + x + 1 cắt nhau tại hai điểm. Kí hiệu (x₁,y₁),(x₂,y₂) là toạ độ của hai điểm đó. Tìm y₁ + y₂

A. y₁ + y₂ = 4     B. y₁ + y₂ = 6    C. y₁ + y₂ = 0    D. y₁ + y₂ = 2

Lời giải 

Phương trình hoành độ giao điểm: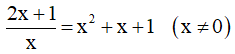  

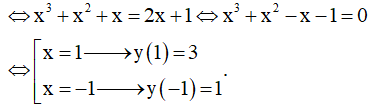
Khi đó y₁ + y₂ = y(1) + y(-1) = 4

Chọn A.

3. Bài tập tự luyện.

Câu 1. Cho hàm số y = (x - 2)(x² + 1) có đồ thị (C). Mệnh đề nào sau đây là đúng?

A. (C) không cắt trục hoành.              B. (C) cắt trục hoành tại một điểm. 

C. (C) cắt trục hoành tại hai điểm.     D. (C) cắt trục hoành tại ba điểm.

Câu 2. Biết rằng đồ thị hàm số y = x³ - 3x² + 2x -1 cắt đồ thị hàm số y = x² - 3x + 1 tại hai điểm phân biệt A và B. Tính độ dài đoạn thẳng AB 

A. AB = 3                 B. AB = 2√2                 C. AB = 2                 D. AB = 1

Câu 3. Đồ thị hàm số y = -x⁴ + 2x² có bao nhiêu điểm chung với trục hoành?

A.0                   B. 2                C. 3                  D. 4

Câu 4. Tìm toạ độ giao điểm M của đồ thị hàm số 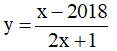 với trục tung.

A. M(0,0).                                   B. M(0,-2018)  

C. M(2018,0)                              D. M(2018,-2018)

Câu 5. Đường thẳng y = 2x + 2016 và đồ thị hàm số 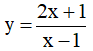 có tất cả bao nhiêu điểm chung?

A. 0.                    B. 1.                   C. 2.                    D. 3.

Câu 6. Gọi M,N là giao điểm của đường thẳng d : y = x + 1 và đồ thị (C) : 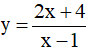. Tìm hoành độ trung điểm x₁ của đoạn thẳng MN.

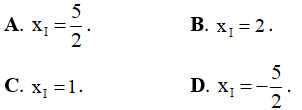
Câu 7. Tìm trên đồ thị hàm số y = -x³ + 3x + 2 (C) hai điểm A,B mà chúng đối xứng nhau qua điểm I(-1;3).

A. A(-1;0) và B(-1;6).               B. A(0;2) và B(-2;4).       

C. A(1;4) và B(-3;2)                 D. Không tồn tại.

Câu 8. Tìm trên đồ thị hàm số 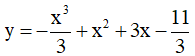 hai điểm phân biệt A,B mà chúng đối xứng nhau qua trục tung.

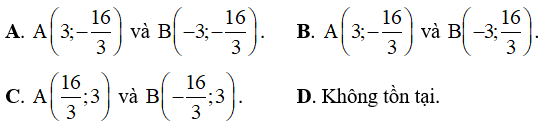
Câu 9. Có bao nhiêu điểm M thuộc đồ thị hàm số 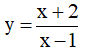 sao cho khoảng cách từ M đến trục Oy bằng hai lần khoảng cách từ M đến trục Oy?

A. 0.                   B. 1                  C. 2.                   D. 3 

Câu 10. Tìm trên đồ thị hàm số 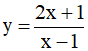 những điểm M sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến trục hoành.

A. M(2;1), M(4;3) .                     B. M(0;-1), M(4;3). 

C. M(0;-1), M(3;2).                     D. M(2;1), M(3;2) .

Câu 11. Số giao điểm của đồ thị hàm số y = x³ - x² và đồ thị hàm số y = -x² + 5x là

A. 2.                    B. 3.                     C. 1.                     D. 0.

Câu 12. Số giao điểm của đồ thị hàm số y = -x² + 3x và đồ thị hàm số y = x³ - x² là

A. 1.                     B. 0.                    C. 2.                    D. 3.  

Đáp án

1	2	3	4	5	6	7	8	9	10	11	12
B	D	C	B	C	C	B	B	C	B	B	D

 

Dạng 2. Tìm m để sự tương giao của các đồ thị hàm số thoả mãn điều kiện cho trước.

1. Phương pháp giải.

BÀI TOÁN 1: TƯƠNG GIAO CỦA ĐỒ THỊ HÀM BẬC 3.

Phương pháp 1: Bảng biến thiên (đồ thị hàm số).

+) Lập phương trình hoành độ giao điểm dạng F(x,m) = 0 (phương trình ẩn x tham số m)

+) Cô lập m đưa phương trình về dạng m = f(x) 

+) Lập BBT cho hàm số y = = f(x) .

+) Dựa và giả thiết và BBT từ đó suy ra m.

* Dấu hiệu: Sử dụng phương pháp bảng biến thiên khi m độc lập với x. 

Phương pháp 2: Nhẩm nghiệm – tam thức bậc 2.

+) Lập phương trình hoành độ giao điểm F(x,m) = 0 

+) Nhẩm nghiệm: (Khử tham số). Giả sử x = x₀ là 1 nghiệm của phương trình. 

+) Phân tích: F(x,m) = 0 ⇔ (x - x₀).g(x) = 0 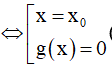(là g(x) = 0 là phương trình bậc 2 ẩn x tham số m ).

+) Dựa vào yêu cầu bài toán đi xử lý phương trình bậc 2: g(x) = 0.

Phương pháp 3: Cực trị.

* Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm.

* Quy tắc:

- Lập phương trình hoành độ giao điểm F(x,m) = 0 (1). Xét hàm số y = F(x,m) .

- Để (1) có đúng 1 nghiệm thì đồ thị y = F(x,m) cắt trục hoành tại đúng 1 điểm. (2TH)

+ Hoặc hàm số luôn đơn điệu trên R ⇔ hàm số không có cực trị ⇔ y' = 0 hoặc vô nghiệm hoặc có nghiệm kép ⇔ Δ_y ≤ 0 

+ Hoặc hàm số có CĐ, CT và y_cđ.y_ct > 0 (hình vẽ)

                   

- Để (1) có đúng 3 nghiệm thì đồ thị y = F(x,m) cắt trục hoành tại 3 điểm phân biệt ⇔ Hàm số có cực đại, cực tiểu và y_cđ.y_ct < 0.

                              

- Để (1) có đúng 2 nghiệm thì đồ thị y = F(x,m) cắt trục hoành tại 2 điểm phân biệt ⇔ Hàm số có cực đại, cực tiểu và y_cđ.y_ct = 0.

                        

Mở rộng: Tìm m để đồ thị hàm bậc 3 cắt trục hoành tại 3 điểm lập thành 1 cấp số cộng.

1. Định lí Vi - ét.

*) Cho bậc 2: Cho phương trình ax² + bx + c = 0 có 2 nghiệm x₁, x₂ thì ta có: 

 

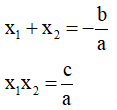
*) Cho bậc 3: Cho phương trình ax³ + bx² + cx + d = 0 có 3 nghiệm x₁, x₂,x₃ thì ta có: 

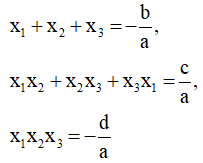
2.Tính chất của cấp số cộng: Cho 3 số a,b,c theo thứ tự đó lập thành 1 cấp số cộng thì: a + c = 2b 

3. Phương pháp giải.

+) Điều kiện cần: 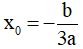 là 1 nghiệm của phương trình. Từ đó thay vào phương trình để tìm m.

+) Điều kiện đủ: Thay m tìm được vào phương trình và kiểm tra.

BÀI TOÁN 2: TƯƠNG GIAO CỦA HÀM SỐ PHÂN THỨC.

Phương pháp : Cho hàm số 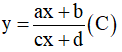 và đường thẳng d : y = px + q. Phương trình hoành độ giao điểm của (C) và (d):  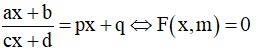(phương trình bậc 2 ẩn x tham số m).

* Các câu hỏi thường gặp:

1. Tìm m để d cắt (C) tại 2 điểm phân biệt ⇔ (1) có 2 nghiệm phân biệt khác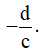 

2. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh phải của (C) ⇔ (1) có 2 nghiệm phân biệt x₁, x₂ và thỏa mãn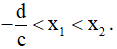 

3. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh trái của (C) ⇔ (1) có 2 nghiệm phân biệt x₁, x₂ và thỏa mãn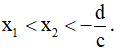 

4. Tìm m để d cắt (C) tại 2 điểm phân biệt thuộc 2 nhánh của (C) ⇔ (1) có 2 nghiệm phân biệt x₁, x₂ và thỏa mãn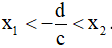 

5. Tìm m để d cắt (C) tại 2 điểm phân biệt A và B thỏa mãn điều kiện hình học cho trước: 

+) Đoạn thẳng AB = k 

+) Tam giác ABC vuông.

+) Tam giác ABC có diện tích S₀ 

 * Chú ý: Công thức tính khoảng cách: 

                          

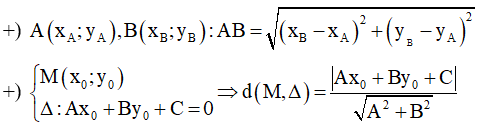
BÀI TOÁN 3: TƯƠNG GIAO CỦA HÀM SỐ BẬC 4.

Phương pháp 1: Nhẩm nghiệm.

- Nhẩm nghiệm: Giả sử x = x₀ là một nghiệm của phương trình.

- Khi đó ta phân tích: f(x,m) = (x² - x₀²)g(x) = 0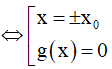  

- Dựa vào giả thiết xử lý phương trình bậc 2 : g(x) = 0

Phương pháp 2: Ẩn phụ - tam thức bậc 2.

- Đặt t = x²,(t > 0). Phương trình: at² + bt + c = 0 (2).

- Để (1) có đúng 1 nghiệm thì (2) có nghiệm t₁,t₂ thỏa mãn: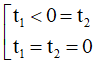  

- Để (1) có đúng 2 nghiệm thì (2) có nghiệm t₁,t₂ thỏa mãn: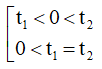  

- Để (1) có đúng 3 nghiệm thì (2) có nghiệm t₁,t₂ thỏa mãn: 0 = t₁ < t₂

- Để (1) có đúng 4 nghiệm thì (2) có nghiệm t₁,t₂ thỏa mãn: 0 < t₁ < t₂ 

Mở rộng: tìm m để (C) : y = ax⁴ + bx² + c cắt trục Ox tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng.

- Đặt t = x²,(t ≥ 0). Phương trình: at² + bt + c = 0 (2).

- Để (1) cắt (Ox) tại 4 điểm phân biệt thì (2) phải có 2 nghiệm dương t₁,t₂ (t₁ < t₂ ) thỏa mãn t₂ = 9t₁ .

- Kết hợp t₂ = 9t₁ với định lý vi – ét tìm được m.

* Giải nhanh :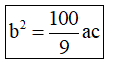  

2. Ví dụ minh hoạ.

Ví dụ 1. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = (x - 1)(x² + mx + m) cắt trục hoành tại ba điểm phân biệt.

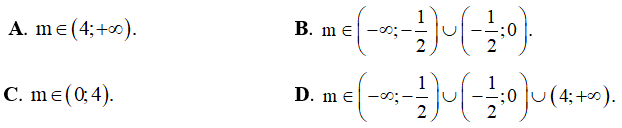
Lời giải

Phương trình hoành độ giao điểm: 

 

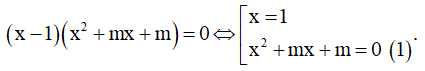
Yêu cầu bài toán ⇔ Phương trình (1) có hai nghiệm phân biệt khác  

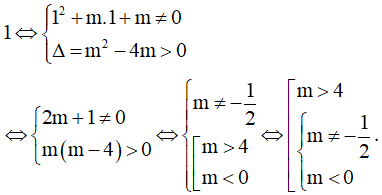
Chọn D.

Ví dụ 2. Tìm giá trị thực của tham số m để phương trình x⁴ - 2x² + 2017 - m = 0 có đúng ba nghiệm.

A. m = 2015.              B. m = 2016.              C. m = 2017.              D. m = 2018. 

Lời giải

Ta có x⁴ - 2x² + 2017 - m = 0 ⇔ x⁴ - 2x² = m - 2017

Xét hàm số y = x⁴ - 2x², có           

 

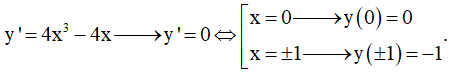
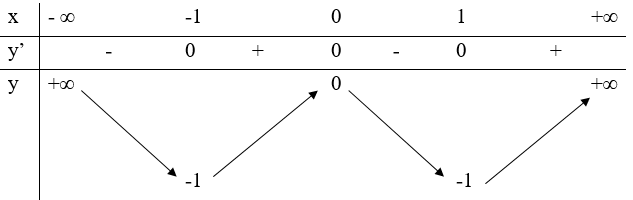
Yêu cầu bài toán ⇔ m - 2017 = y_CĐ ⇔ m - 2017 = 0 ⇔ m = 2017

Chọn D.

Ví dụ 3. Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = 2mx + m + 1 cắt đồ thị hàm số 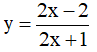 (C) tại hai điểm phân biệt.

A. m = 1             B. m = 0           C. m > 1             D. m < 0  

Lời giải

Phương trình hoành độ giao điểm: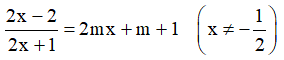  

⇔ 2x - 2 = (2mx + m + 1)(2x + 1) ⇔ 4mx² + 4mx + m + 3 = 0 (∗)     

Để d cắt (C) tại hai điểm phân biệt ⇔ phương trình (∗) có hai nghiệm phân biệt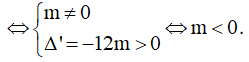 

Chọn D.

3. Bài tập tự luyện.

Câu 1. Với giá trị nào của m thì đường thẳng y = m cắt đường cong y = x³ - 3x² tại ba điểm phân biệt?

A. -4 < m < 0                 B. m > 0              C. m < -4                D.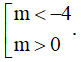  

Câu 2. Cho phương trình 2x³ - 3x² + 2 - 2^1-2m = 0. Với giá trị nào của m thì phương trình đã cho có ba nghiệm phân biệt.

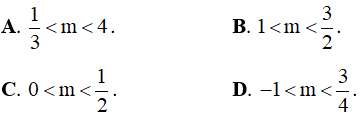
Câu 3. Cho phương trình 2x³ - 3x² = 2m + 1. Với giá trị nào của m thì phương trình đã cho có đúng hai nghiệm phân biệt:

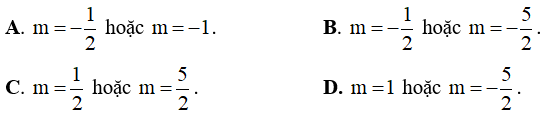
Câu 4. Với giá trị nào của m thì đồ thị hàm số y = x³ - mx² + 4 cắt trục hoành tại ba điểm phân biệt?

A. m ≠ 0                 B. m > 0                  C. m ≠ 3                  D. m > 0 

Câu 5. Phương trình x³ - 3mx + 2 = 0 có một nghiệm duy nhất khi điều kiện của m là:

A. 0 < m < 1 .         B. m < 1.                 C. m ≤ 0.                 D. m > 1 

Câu 6. Đồ thị hàm số y = x³ - (2m + 1)x² + (3m + 1)x - m - 1 luôn cắt trục hoành tại điểm có hoành độ bằng bao nhiêu?

A. x = 2 .               B. x = 1 .                C. x = m .              D. x = 0 . 

Câu 7. Tìm m để đường thẳng d: y = m( x - 1) + 1 cắt đồ thị hàm số d: y = -x³ + 3x - 1 tại ba điểm phân biệt A(1;1),B,C 

Câu 8. Tìm m để đồ thị hàm số y = x³ - 3x² + 2 cắt đường thẳng d: y = m( x - 1) tại ba điểm phân biệt có hoành độ là x₁, x₂, x₃ thỏa mãn x₁² + x₂² + x₃² = 5 .

A. m > -3           B. m = -3             C. m > -2            D. m = -2 

Câu 9. Đường thẳng d : y = x + 4 cắt đồ thị hàm số y = x³ + 2mx² + (m + 3)x + 4 tại ba điểm phân biệt A(0;4), B, C sao cho tam giác MBC có diện tích bằng 4, với M(1;3). Tập tất cả các giá trị của m nhận được là:

A. m = 2 hoặc m = 3.                B. m = 3

C. m = -2 hoặc m = -3              D. m = -2 hoặc m = 3

Câu 10. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = mx - m + 1 cắt đồ thị của hàm số y = x³ - 3x² + x + 2 tại ba điểm A, B, C phân biệt sao cho AB = BC 

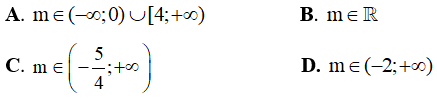
Câu 11. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = -mx cắt đồ thị của hàm số y = x³ - 3x² - m + 2 tại ba điểm phân biệt A, B, C sao cho AB = BC.

A. m = 1                                    B. m ∈ (-∞;-1)                

C. m ∈ (-∞;+∞)                          D. m ∈ (1;+∞) 

Câu 12. Với điều kiện nào của k thì phương trình 4x²(1 - x²) = 1 - k có bốn nghiệm phân biệt?

A. 0 < k < 2 .                    B. k < 3.                C. -1 < k < 1.                  D. 0 < k < 1. 

Câu 13. Cho phương trình x⁴ - 2x² + 2017 - m = 0. Với giá trị nào của m thì phương trình đã cho có đúng ba nghiệm ?

A. m = 2015 .                           B. m = 2016                   

C. m = 2017.                            D. m = 2018. 

Câu 14. Đường thẳng y = m và đường cong y = x⁴ - 2x² - 3 có hai điểm chung khi:

A. m > -3 hoặc m = -4 .            B. m > -4 hoặc m = -3 

C. -4 < m < -3 .                         D. m > -4

Câu 15. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 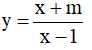 cắt đường thẳng y = 2x + 1 tại hai điểm phân biệt.

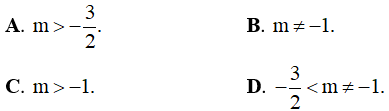
Câu 16. Tìm tất cả các giá trị của tham số m để đường thẳng y = x - 2m cắt đồ thị hàm số 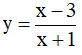 tại hai điểm phân biệt có hoành độ dương.

Câu 17. Gọi d là đường thẳng A(1;0) đi qua và có hệ số góc m. Tìm các giá trị của tham số m để d cắt đồ thị hàm số 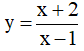 tại hai điểm phân biệt M, N thuộc hai nhánh của đồ thị.

A. m ≠ 0              B. m > 0                C. m < 0             D. 0 < m ≠ 1

Câu 18. Tìm tất cả các giá trị của tham số m để đường thẳng d : y = -x + m cắt đồ thị hàm số 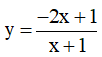 tại hai điểm A, B sao cho AB = 2√2 .

A. m = 1; m = -2.                      B. m = 1; m = -7. 

C. m = -7; m = 5.                      D. m = 1; m = -1.

Câu 19. Tìm tất cả các giá trị của tham số m để đường thẳng d : y = x - m + 2 cắt đồ thị hàm số 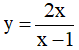 tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất.

A. m = -3            B. m = -1            C. m = 3              D. m = 1. 

Câu 20. Tìm tất cả các giá trị của tham số k sao cho đường thẳng d : y = x + 2k + 1 cắt đồ thị hàm số 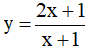 tại hai điểm phân biệt A và B sao cho các khoảng cách từ A và B đến trục hoành là bằng nhau.

A. k = -1 .              B. k = -3.               C. k = -4              D. k = -2. 

Câu 21. Tìm tất cả các giá trị của m để đường thẳng d : y = x + m cắt đồ thị hàm số 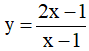 tại hai điểm phân biệt A, B sao cho tam giác OAB vuông tại O(0;0).

A. m = -2             B. 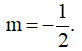C. m = 0              D. m = 1 

Câu 22. Tìm tất cả các giá trị của tham số m để đường thẳng cắt đồ thị hàm số 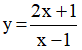 tại hai điểm A và B phân biệt sao cho trọng tâm tam giác OAB thuộc đường thẳng Δ : x - 2y - 2 = 0, với O là gốc tọa độ.

Câu 23. Tìm tất cả các giá trị của m để đường thẳng d : y = 2x + 3m cắt đồ thị hàm số 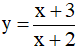 tại hai điểm phân biệt A và B sao cho 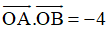, với O là gốc tọa độ.

Câu 24. Tìm tất cả các giá trị của tham số m sao cho đường thẳng d : y = x + m cắt đồ thị hàm số 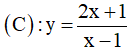 tại hai điểm phân biệt M và N sao cho diện tích tam giác IMN bằng 4, với I là tâm đối xứng của (C).

A. m = 3; m = 5                       B. m = 3; m = -3  

C. m = 3; m = -1                      D. m = -3; m = -1

Câu 25. Cho hàm số y = f(x) xác định trên R\ và liên tục trên từng khoảng xác định, có bảng biến thiên như sau:

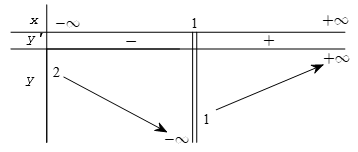
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f(x) cắt đường thẳng y = 2m - 1 tại hai điểm phân biệt. 

Câu 26. Cho hàm số y = f(x), xác định trên R\{-1;1} liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

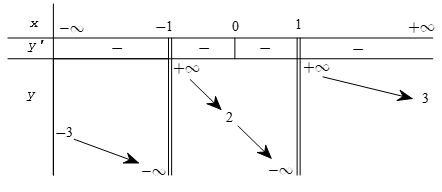
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng y = 2m + 1 cắt đồ thị hàm số đã cho tại hai điểm phân biệt. 

A. m ≤ -2           B. m ≥ 1             C. m ≤ -2,m ≥ 1       D. m < -2,m > 1 

Câu 27. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x³ - 3mx² + 6mx - 8 cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành cấp số cộng.

A. m = 1                B. m = 2;m = -1               C. m = -1              D. m = 2

Câu 28. Cho hàm số y = x⁴ - m(m + 1)x² + m³ với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại bốn điểm phân biệt.

A. m > 1              B. m > -√2            C. m > √2             D. 0 < m ≠ 1 

Câu 29. Cho hàm số y = -x⁴ + 2(m + 2)x² - 4 - m với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số đã cho không có điểm chung với trục hoành?

A. 1                   B. 2                  C. 3                   D. 4 

Câu 30. Cho hàm số y = x⁴ - 2(m + 4)x² + m² với m là tham số thực. Tìm tất cả các giá trị của m đề đồ thị hàm số đã cho cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.

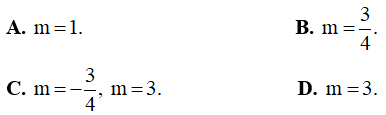
Đáp án

Phần 8: Các dạng bài tập tiếp tuyến của đồ thị hàm số

A. LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI.

1. Phương pháp giải.

Bài toán 1: Viết phương trình tiếp tuyến của đồ thị hàm số (C) : y = f(x) tại điểm M(x₀,y₀) thuộc đồ thị hàm số.

Cho hàm số (C) : y = f(x) và điểm M(x₀,y₀) ∈ (C). Viết phương trình tiếp tuyến với (C) tại M.

Bước 1: Tính đạo hàm y'. Tìm hệ số góc của tiếp tuyến là y'(x₀).

Bước 2: Phương trình tiếp tuyến tại điểm M là: y = y'(x₀)(x - x₀) + y₀ 

Lưu ý:

- Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ x₀ thì khi đó ta tìm y₀ bằng cách thế vào hàm số ban đầu, tức y₀ = f(x₀) Nếu đề cho y₀ ta thay vào hàm số để giải ra x₀

- Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị (C) : y = f(x) và đường thẳng d : y = ax + b. Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm giữa d và (C) 

Bài toán 2: Viết phương trình tiếp tuyến của đồ thị hàm số (C) : y = f(x) có hệ số góc k cho trước.

Bước 1: Gọi (Δ) là tiếp tuyến cần tìm có hệ số góc k. 

Bước 2: Giả sử M(x₀,y₀) là tiếp điểm. Khi đó x₀ thỏa mãn: y'(x₀) = k (*) .

Bước 3: Giải (*) tìm x₀. Suy ra y₀ = f(x₀)

Bước 4: Phương trình tiếp tuyến cần tìm là: y = k(x - x₀) + y₀ 

Lưu ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:

- Tiếp tuyến d // Δ : y = ax + b => hệ số góc của tiếp tuyến là k = a 

- Tiếp tuyến d ⊥ Δ : y = ax + b,(a ≠ 0) => hệ số góc của tiếp tuyến là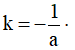  

- Tiếp tuyến tạo với trục hoành một góc α thì hệ số góc của tiếp tuyến d là k = ±tan α

Bài toán 3: Viết phương trình tiếp tuyến của đồ thị hàm số (C) : y = f(x) biết tiếp tuyến đi qua điểm A(x_A, y_A)

Cách 1.

Bước 1: Phương trình tiếp tuyến đi qua A(x_A, y_A) hệ số góc k có dạng

d : y = k(x - x_A) + y_A (∗)   

Bước 2: d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:

 

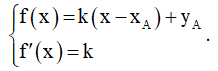
Bước 3: Giải hệ này tìm được x suy ra k và thế vào phương trình (∗), ta được tiếp tuyến cần tìm.

Cách 2.

Bước 1. Gọi M(x₀, f(x₀)) là tiếp điểm và tính hệ số góc tiếp tuyến k = y'(x₀) = f'(x₀) theo x₀ 

Bước 2. Phương trình tiếp tuyến có dạng: d : y = y'(x₀)(x - x₀) + y₀(∗∗). Do điểm A(x_A, y_A) ∈ d nên y_A = y'(x₀)(x - x₀) + y₀ giải phương trình này ta tìm được x₀.

Bước 3. Thế x₀ vào (∗∗) ta được tiếp tuyến cần tìm.

Bài toán 4 : Viết phương trình tiếp tuyến chung của hai đồ thị hàm số (C₁) : y = f(x) và (C₂) : y = g(x).

Bước 1. Gọi d tiếp tuyến chung của (C₁), (C₂) và x₀ là hoành độ tiếp điểm của d và (C₁) thì phương trình d có dạng y = f'(x₀)(x - x₀) + f(x₀) (∗∗∗) 

Bước 2. Dùng điều kiện tiếp xúc của d và (C₂), tìm được x₀

Bước 3. Thế x₀ vào (∗∗∗) ta được tiếp tuyến cần tìm.

Lưu ý:

- Hệ số góc của tiếp tuyến với (C) tại điểm M(x₀,y₀) thuộc (C) là: k = y'(x₀)  

- Cho đường thẳng (d) : y = ax + b 

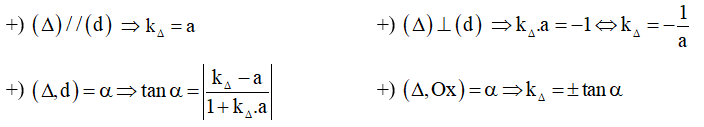
- Tiếp tuyến tại các điểm cực trị của đồ thị (C) có phương song song hoặc trùng với trục hoành.

- Cho hàm số bậc 3: y = ax³ + bx² + cx + d (a ≠ 0) 

+) Khi a > 0: Tiếp tuyến tại tâm đối xứng của (C) có hệ số góc nhỏ nhất.

+) Khi a < 0: Tiếp tuyến tại tâm đối xứng của (C) có hệ số góc lớn nhất.

2. Công thức tính nhanh.

Bài toán 1: Cho hàm số 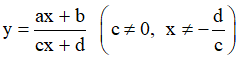 có đồ thị (C). Phương trình tiếp tuyến Δ tại M thuộc (C) và I là giao điểm 2 đường tiệm cận. Ta luôn có:

- Nếu Δ ⊥ IM thì chỉ tồn tại 2 điểm M thuộc 2 nhánh của đồ thị (C) đối xứng qua I và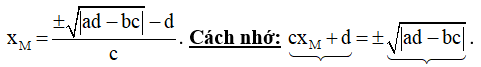 

- M luôn là trung điểm của AB (với A,B là giao điểm của Δ với 2 tiệm cận).

- Diện tích tam giác IAB không đổi với mọi điểm M và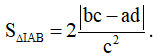 

- Nếu E,F thuộc 2 nhánh của đồ thị (C) và E,F đối xứng qua I thì tiếp tuyến tại E,F song song với nhau (suy ra một đường thẳng d đi qua E,F thì đi qua tâm I).

Chứng minh:

- Ta có 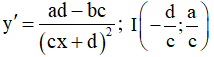 là giao điểm của 2 tiệm cận.

- Gọi 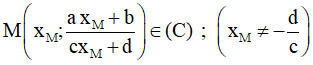. Phương trình tiếp tuyến tại M có dạng:

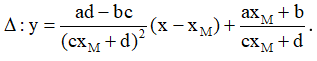
Ta có:

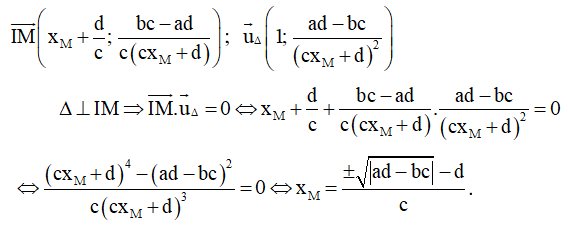
Lại có: 

- Giao điểm của Δ với tiệm cận ngang là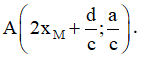 

- Giao điểm của Δ với tiệm cận đứng là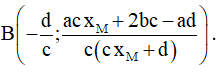 

- Xét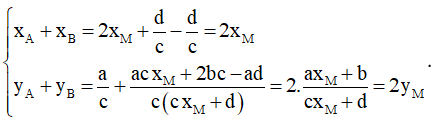 

Vậy M luôn là trung điểm của AB.

Ta có:

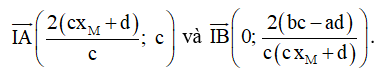
ΔIAB vuông tại I 

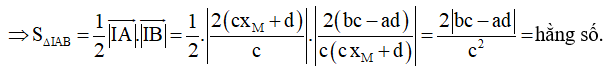
Vậy diện tích ΔIAB không đổi với mọi điểm M.

Ta có: 

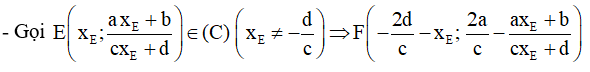
( E,F đối xứng qua I).

- Phương trình tiếp tuyến tại E có hệ số góc: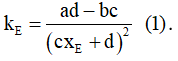 

- Phương trình tiếp tuyến tại F có hệ số góc:

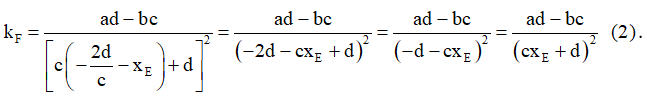
Từ (1) và (2) suy ra k_E = k_F .

Bài toán 2: Cho hàm số 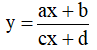 có đồ thị là (C), (c ≠ 0, ad - bc ≠ 0) . Gọi điểm M(x₀;y₀) trên (C) biết tiếp tuyến của (C) tại điểm M cắt các trục Ox, Oy lần lượt tại A,B sao cho OA = nOB . Khi đó x₀ thoả mãn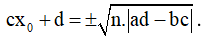 

Chứng minh:

- Xét hàm số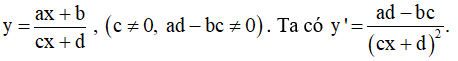 

- Gọi 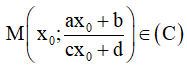 là điểm cần tìm. Gọi Δ tiếp tuyến với (C) tại M ta có phương trình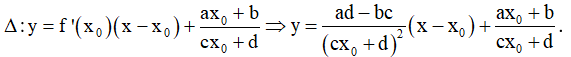 

 

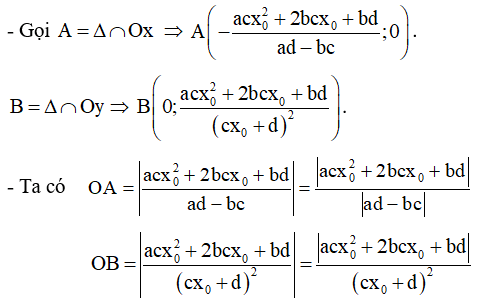
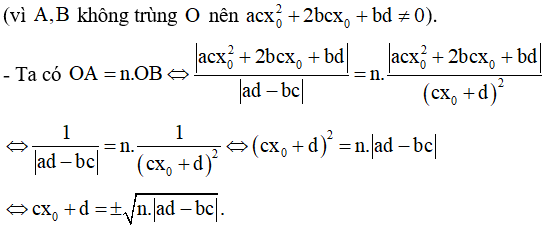
B. VÍ DỤ MINH HOẠ.

Ví dụ 1.Tiếp tuyến của đồ thị hàm số y = x⁴ + 2x² - 3 tại điểm H có tung độ bằng 21 có phương trình là:

Lời giải

Gọi H(x₀ ;y₀) ta có y₀ = 21 nghĩa là x₀⁴ + 2x₀² - 3 = 21 

Giải phương trình 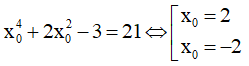. Đồng thời y' = 4x³ + 4x, suy ra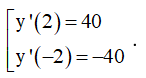  

Vậy có hai tiếp tuyến cần tìm là y = 40x - 59 và y = -40x - 101.

Chọn B.

Ví dụ 2. Phương trình tiếp tuyến của đồ thị hàm số y = 3x³ - x² - 7x + 1 tại điểm A(0;1) là

A. y = x + 1.                   B. y = -7x + 1                 C. y = 1                 D. y = 0

Lời giải

Theo giả thiết ta có x₀ = 0; y₀ = 1 và y' = 9x² - 2x - 7 → y'(0) = -7

Vậy phương trình tiếp tuyến là y = -7x + 1

Chọn B.

Ví dụ 3. Cho hàm số 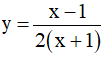 có đồ thị là (C). Gọi điểm M(x₀;y₀) với x₀ > -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A,B và tam giác OAB có trọng tâm G nằm trên đường thẳng d : 4x + y = 0. Hỏi giá trị của x₀ + 2y₀ bằng bao nhiêu?

Lời giải

- Gọi 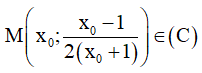 với x₀ ≠ -1 là điểm cần tìm.

- Gọi Δ tiếp tuyến của (C) tại M ta có phương trình.

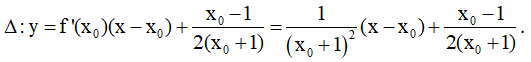
- Gọi Δ = Δ ∩ Ox =>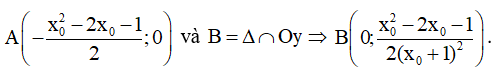  

- Khi đó Δ tạo với hai trục tọa độ ΔOAB có trọng tâm là

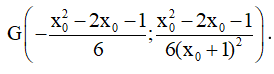
- Do G thuộc đường thẳng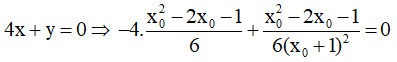    

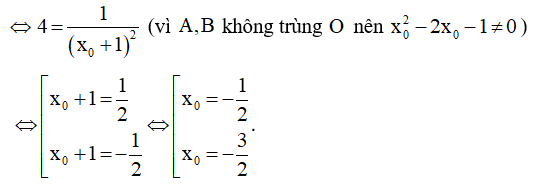
Vì x₀ > -1 nên chỉ chọn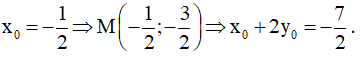 

Chọn A.

C. BÀI TẬP TỰ LUYỆN.

Câu 1. Phương trình tiếp tuyến của đường cong (C) : y = x³ - 2x + 3 tại điểm M(1;2) là:

A. y = 2x + 2 .        B. y = 3x - 1          C. y = x + 1           D. y = 2 - x

Câu 2. Tiếp tuyến của đồ thị hàm số 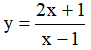 tại điểm có hoành độ bằng 2, có hệ số góc:

A. -1 .                    B. -3 .                      C. 3.                   D. 5.

Câu 3. Gọi (C) là đồ thị của hàm số 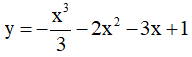. Có hai tiếp tuyến của (C) cùng có hệ số góc bằng  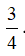Đó là các tiếp tuyến:

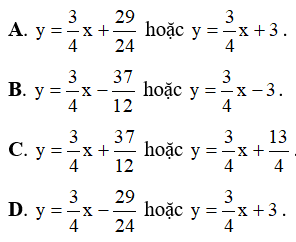
Câu 4. Cho hàm số y = 2x³ + 3x² - 4x + 5 có đồ thị là (C). Trong số các tiếp tuyến của (C), có một tiếp tuyến có hệ số góc nhỏ nhất. Hệ số góc của tiếp tuyến này bằng:

A. -3,5 .              B. -5,5              C. -7,5             D. -9,5

Câu 5. Cho hàm số y = x³ - 6x² + 9x có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng d : y = 9x có phương trình:

A. y = 9x + 40.          B. y = 9x - 40           C. y = 9x + 32.          D. y = 9x - 32.

Câu 6. Cho hàm số y = x³ + 3x² + 1 có đồ thị là (C). Gọi Δ là tiếp tuyến của (C) tại điểm A(1;5) và B là giao điểm thứ hai của   với V. Diện tích tam giác OAB bằng:

A. 5.                   B. 6.                    C. 12.                 D. 6√82.

Câu 7. Cho hàm số 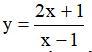 có đồ thị (C). Gọi d là tiếp tuyến của (C), biết d đi qua điểm A(4;-1). Gọi M là tiếp điểm của d và (C), toạ độ điểm M là:

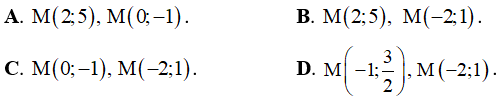
Câu 8. Cho hàm số 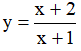 có đồ thị (C). Trong tất cả các tiếp tuyến của (C), tiếp tuyến thỏa mãn khoảng cách từ giao điểm của hai tiệm cận đến nó là lớn nhất, có phương trình:

A. y = -x + 2 hoặc y = -x - 2.              B. y = -x + 2 hoặc y = -x - 1.

C. y = x + 2 hoặc y = x - 2.                D. y = -x + 1 hoặc y = -x - 1.

Câu 9. Từ điểm 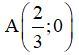 kẻ đến đồ thị hàm số  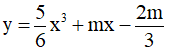hai tiếp tuyến vuông góc nhau thì tập tất cả các giá trị của m bằng:

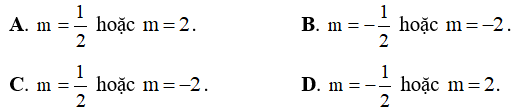
Câu 10. Cho hàm số y = x⁴ - 2m²x² + 2m + 1 có đồ thị (C). Tập tất cả các giá trị của tham số m để tiếp tuyến của (C) tại giao điểm của (C) và đường thẳng d : x = 1 song song với đường thẳng Δ : y = -12x + 4 là?

A. m = 0 .            B. m = 1.             C. m = ±2.          D. m = 3 

Câu 11. Cho hàm số 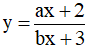 có đồ thị là (C). Tại điểm M(-2;-4) thuộc (C), tiếp tuyến của (C) song song với đ­ường thẳng d : 7x - y + 5 = 0. Khi đó biểu thức liên hệ giữa a và b là:

A. b - 2a = 0             B. a - 2b = 0            C. b - 3a = 0          D. a - 3b = 0

Câu 12. Cho hàm số 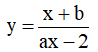 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M(1;-2) song song với đường thẳng d : 3x + y - 4 = 0. Khi đó giá trị của a + b bằng:

A. 2.                   B. 1.                    C. -1.                  D. 0.

Câu 13. Cho hàm số 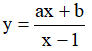 có đồ thị là (C). Nếu (C) đi qua A(3;1) và tiếp xúc với đư­ờng thẳng d : y = 2x - 4, thì các cặp số (a;b) theo thứ tự là:

A. (2;4) hoặc (10;28).                  B. (2;-4) hoặc (10;-28).

C. (-2;4) hoặc (-10;28)                D. (-2;-4) hoặc (-10;-28).

Câu 14. Cho hàm số 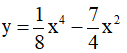 có đồ thị (C) .Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M(x₁,y₁), N(x₂, y₂) (M,N khác A) thỏa mãn  

A. 0.                     B. 2                      C. 3                      D. 1

Câu 15. Tiếp tuyến của đồ thị hàm số y = -x³ + 3x - 2 tại điểm D có hoành độ bằng 2 có phương trình là

A. y = -9x + 14 .                  B. y = 9x + 14.      

C. y = -9x + 22.                   D. y = 9x + 22

Câu 16. Tiếp tuyến của đồ thị hàm số 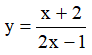 tại điểm I có tung độ bằng 1 có phương trình là

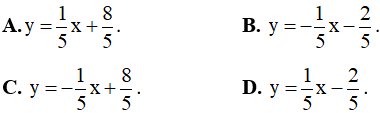
Câu 17. Tiếp tuyến của đồ thị hàm số 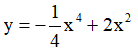 có hệ số góc bằng x + 2y - 9 = 0 có phương trình là

A. y = -48x + 192 .               B. y = -48x + 160                            

C. y = -48x - 160.                 D. y = -48x - 192

Câu 18. Viết phương trình tiếp tuyến của đồ thị hàm số 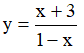 biết tiếp tuyến có hệ số góc bằng 4.

Câu 19. Cho hàm b y = 2x³ - 3x - 1 có đồ thị là (C). Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x + 21y - 2 = 0 có phương trình là:

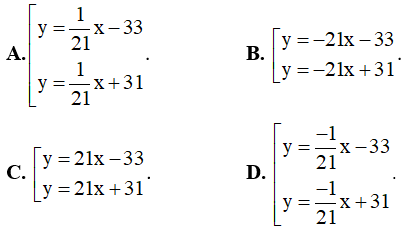
Câu 20. Có bao nhiêu tiếp tuyến của đồ thị hàm số y = x⁴ - 4x² tại giao điểm của đồ thị với trục Ox ?

A. 4.                           B. 2.                       C. 1.                       D. 3.

Câu 21. Gọi d là tiếp tuyến của đồ thị hàm số (C):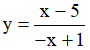 tại giao điểm A của (C) và trục hoành. Khi đó, phương trình của đường thẳng d là

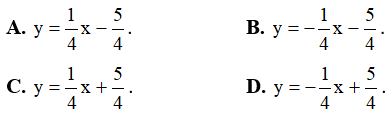
Câu 22. Phương trình tiếp tuyến của đồ thị hàm số (C): 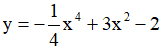 tại giao điểm M của (C) với trục tung là

Câu 23. Cho hàm số y = x³ - 3x² + 6x + 1 có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất có phương trình là

A. y = -3x + 2 .                    B. y = 3x + 2.       

C. y = -3x + 8.                     D. y = 3x + 8.

Câu 24. Cho hàm số y = -x³ + 6x² + 3x - 1 có đồ thị (C).Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc lớn nhất có phương trình là

A. y = 15x + 55 .                   B. y = -15x - 5   

C. y = 15x - 5.                       D. y = -15x + 55.

Câu 25. Cho hàm số 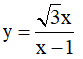 có đồ thị (C). Tiếp tuyến của (C) tạo với trục hoành góc 60⁰ có phương trình là

Câu 26. Cho hàm số  y = x³ - 3mx² + 3(m+ 1)x + 1 (1), m là tham số. Kí hiệu (C_m) là đồ thị hàm số (1) và K là điểm thuộc (C_m), có hoành độ bằng -1. Tập tất cả các giá trị của tham số m để tiếp tuyến của (C_m) tại điểm K song song với đường thẳng d : 3x + y = 0 là

Câu 27. Cho hàm số y = 3x - 4x³ có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?

A. 0.                          B. 3.                     C. 2.                     D. 1.

Câu 28. Cho hàm số y = x³ - x² + x + 1 có đồ thị (C). Tiếp tuyến tại điểm N của (C) cắt đồ thị (C) tại điểm thứ hai là M(-1;-2). Khi đó tọa độ điểm N là

A. (-1;-4).                     B. (2;5).                     C. (1;2).                   D. (0;1).

Câu 29. Cho hàm số 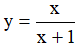 có đồ thị (C) và gốc tọa độ O. Gọi Δ là tiếp tuyến của (C), biết Δ cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân. Phương trình Δ là

A. y = x + 1 .                  B. y = x + 4                     C. y = x - 4                   D. y = x 

Câu 30. Cho hàm số y = -x⁴ - x² + 6 có đồ thị (C). Tiếp tuyến của đồ thị (C) cắt các trục Ox, Oy lần lượt tại hai điểm A, B sao cho OB = 36OA có phương trình là:

Câu 31. Cho hàm số 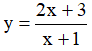 có đồ thị là (C). Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d₁ : 3x + 4y - 2 = 0 bằng 2.

A. 2.                      B. 3.                     C. 4.                     D. 0.

Câu 32. Cho hàm số 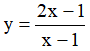 có đồ thị là (C). Gọi I là giao điểm hai tiệm cận của (C). Tìm điểm M thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI ?

Câu 33. Cho hàm số 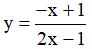 có đồ thị là (C), đường thẳng d : y = x + m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A,B. Gọi k₁,k₂ lần lượt là hệ số góc của các tiếp tuyến với (C) tại  . Tìm m để tổng k₁ + k₂ đạt giá trị lớn nhất.

A. m = -1 .                   B. m = -2.                     C. m = 3.                   D. m = -5.

Câu 34. Cho hàm số 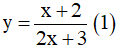.Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A,B và tam giác OAB cân tại gốc tọa độ O.

A. y = -x - 2 .                 B. y = -x               C. y = -x + 2            D. y = -x + 1

Câu 35. Cho hàm số 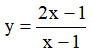 có đồ thị (C). Lập phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến này cắt các trục   lần lượt tại các điểm Ox và Oy thoả mãn OA = 4OB.

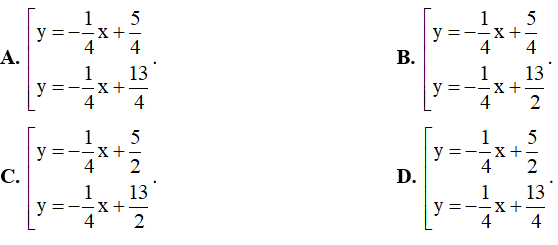
Câu 36. Cho hàm số 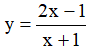 có đồ thị (C). Biết khoảng cách từ I(-1;2) đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất?

A. 3e .                      B. 2e .                     C. e .                     D. 4e .

Câu 37. Cho hàm số 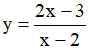 có đồ thị (C). Biết tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A,B sao cho ngắn nhất. Khi đó, độ dài lớn nhất của vectơ  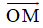gần giá trị nào nhất ?

A. 7.                        B. 5.                     C. 6.                     D. 4.

Câu 38. Cho hàm số 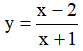 có đồ thị (C). Phương trình tiếp tuyến Δ của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị (C) đến Δ bằng?

A. √3 .                    B. 2√6 .                C. 2√3 .               D. √6 .

Câu 39. Cho hàm số 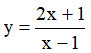 có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến Δ của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến Δ gần giá trị nào nhất?

A. 6.                       B. 4.                     C. 3.                     D. 5.

Câu 40. Cho hàm số 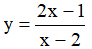 có đồ thị (C). Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến Δ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến Δ của (C) tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào?

A. (27;28) .              B. (28;29).                C. (26;27) .              D. (29;30) .

Đáp án

1	2	3	4	5	6	7	8	9	10
C	B	C	B	D	C	B	A	B	C
11	12	13	14	15	16	17	18	19	20
D	A	B	B	A	C	B	D	C	D
21	22	23	24	25	26	27	28	29	30
D	C	B	A	C	B	C	C	B	C
31	32	33	34	35	36	37	38	39	40
C	C	A	A	A	C	D	D	D	A