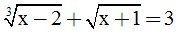Tài liệu Bộ đề thi Toán lớp 9 Giữa học kì 1 Tự luận năm học 2022 - 2023 gồm 7 đề thi tổng hợp từ đề thi môn Toán 9 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Giữa học kì 1 Toán lớp 9. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi giữa kì 1 Toán 9 bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

Câu 1 (2,0 điểm).

1. Thực hiện phép tính.

 

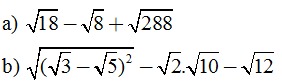
2. Tìm điều kiện của x để các biểu thức sau có nghĩa: 

 

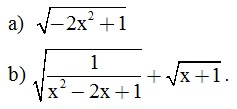
Câu 2 (2 điểm). Giải phương trình:

 

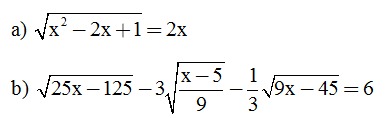
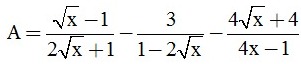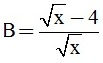Câu 3. (2 điểm). Cho biểu thức: và  với x > 0; x ≠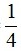  

1. Tính giá trị của biểu thức B biết  .

2. Rút gọn A .

3. Đặt P = A.B . Tìm x để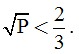  

Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a) Tính độ dài các đoạn thẳng AB, AC, AH.

b) Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC

c) Chứng minh rằng: S_BHD = 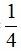S_BKC.cos²∠ABD. 

Bài 5 (0,5 điểm). Cho biểu thức P = x³ + y³ - 3(x + y) + 1993 . Tính giá trị biểu thức P với: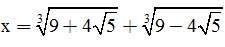  và 

...........................................................................

Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 2

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

Câu 1. (2 điểm). Thực hiện phép tính để rút gọn biểu thức sau :

 

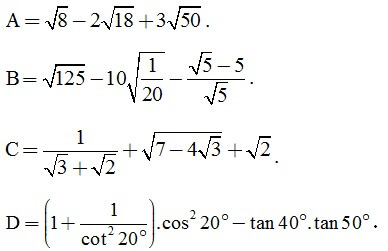
Câu 2. (2 điểm) Cho biểu thức:

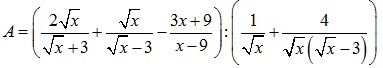 với x > 0; x ≠ 9

a) Rút gọn .

b) Tìm để   .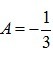

c) Tìm các giá trị của x để  .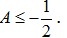

d) Tìm các giá trị của x để A nhận giá trị nguyên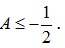  

Câu 3. (2 điểm). Giải các phương trình sau:

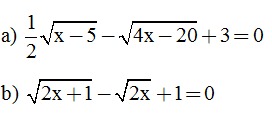
Câu 4. (3,5 điểm). 

1) Một con thuyền đi từ bến sông A tới bến sông B với vận tốc trung bình 4 km/h trong 10 phút. Biết đường đi của con thuyền là AB, tạo với bờ sông một góc bằng 60^o. Tính chiều rộng AH của khúc sông.

 

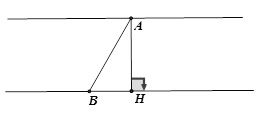
2)   Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm; BC = 5cm . 

a) Hãy giải tam giác ABC (góc làm tròn đến độ).

b) Kẻ BD là phân giác của góc B. Trên cạnh AB lấy điểm E sao cho AE = 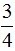AB   . Hãy tính độ dài các đoạn thẳng AD, DE .

c) Đường thẳng DE cắt BC tại F. Tính tỷ số   .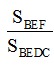

Câu 5. (0,5 điểm). Cho các số thỏa mãn và 0 < x; y < 2 và  .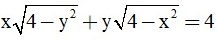

Tìm giá trị nhỏ nhất của biểu thức P = x⁶ + y⁶  

...........................................................................

Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 3

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 3)

Câu 1. (2,0 điểm). Thực hiện phép tính và rút gọn các biểu thức sau:

 

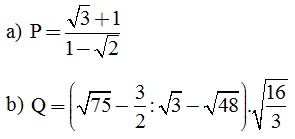
Câu 2. (2,0 điểm). Giải các phương trình sau:

 

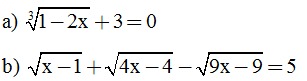
Câu 3. (2,0 điểm). Cho biểu thức 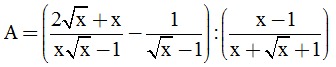 (với x > o. x ≠ 1 )

a) Rút gọn biểu thức A.

b) Tính A khi x = 5 + 2√3 .

c) Tìm x để |A| < 1 

Câu 4. (3,5 điểm) Cho tam giác ABC vuông tại A và đường cao AH ( H ∈ BC) .

1) (1 điểm) Cho AH = 6; BH = 3 . Tính BC và số đo ∠ABC (góc làm tròn đến phút).

2) (1 điểm) Đường thẳng vuông góc với BC tại B cắt tia CA tại K. Hạ AE ⊥ BK (E ∈ BK) . Chứng minh rằng: AK.AC = EH²  , từ đó suy ra BH.HC + BE.EK = AK.AC.

3) (1 điểm) Giả sử cạnh BC cố định và BC = a không đổi, xác định vị trí của điểm H trên BC sao cho tứ giác AHBE có diện tích lớn nhất.

Câu 5. (0,5 điểm) 

Cho ba số thực dương thỏa mãn x + y ≤ z . Chứng minh rằng:

...........................................................................

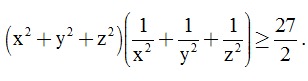
Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 4

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 4)

Bài 1 (2,5 điểm). Cho hai biểu thức : 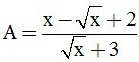 và 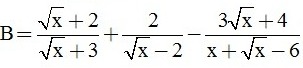 với ( x ≥ 0, x ≠ 4)

a) Tính giá trị của A khi x = 3 + 2√2 

b) Rút gọn biểu thức B.

c) Cho biểu thức M = B : A ( x ≥ 0, x ≠ 4). Tính giá trị của x để M có giá trị lớn nhất.

Bài 2 (2,0 điểm). Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 

y = (m + 1)x + m + 3  ( m ≠ -1)

a) Tìm m để đường thẳng (d) đi qua A(-2; 3). 

b) Với giá trị của m tìm được ở câu a) hãy vẽ đồ thị hàm số.

c) Tìm khoảng cách lớn nhất từ gốc tọa độ đến đường thẳng (d) khi m thay đổi.

Bài 3 (1,5 điểm)

a) Giải phương trình:  

b) Rút gọn:  

Bài 4 (3,5 điểm). Cho cân tại A, AH là đường cao. Đường thẳng qua C vuông góc AC cắt AH ở O. Vẽ đường tròn tâm O bán kính OC cắt tia Ax nằm trong góc BAC tại M và N (AM < AN). Gọi K là chân đường vuông góc kẻ từ O lên Ax.

a) Chứng minh: Bốn điểm A, C, O, K thuộc một đường tròn.

b) Biết AH = 24cm, OH = 6cm. Tính chu vi tam giác ABC.

c) Gọi Ax cắt BC tại I. Chứng minh: AI.AK = AC² .

d) Gọi G là trọng tâm tam giác CMN. Khi Ax di động thì G chạy trên đường nào.

Bài 5 (0,5 điểm). Cho các số thực dương x, y, z thỏa mãn √x + √y + √z = 1 .

Tìm GTNN của biểu thức:

   .

 

...........................................................................

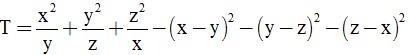Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 5

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 5)

đề 3

Câu 1 (3 điểm). Thực hiện phép tính:

 

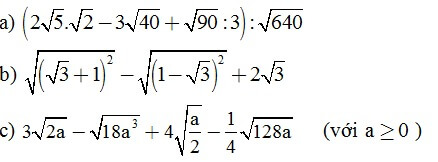
Câu 2 (2,5 điểm). Giải phương trình:

 

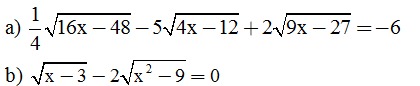
Câu 3 (3 điểm). Cho hai biểu thức: 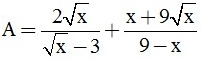và 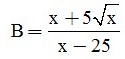   với x ≥ 0, x ≠ 9, x ≠ 25.

a) Rút gọn các biểu thức A và B.

b) Tính B khi x = 6 - 2√5 

c) So sánh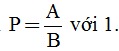   

Câu 4 (3,5 điểm). Cho tam giác ABC vuông tại A có ∠C = 30^o  , BC = 18cm, đường cao AH.

a) Tính độ dài AB, AC, AH (Kết quả để dưới dạng căn thức thu gọn)

b) Chứng minh rằng: cosC.cosB =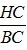  

c) Gọi Bx, By lần lượt là tia phân giác trong và tia phân giác ngoài của góc B. Kẻ AK vuông góc với Bx, AE vuông góc với By (K thuộc Bx, E thuộc By). Chứng minh rằng KE // BC.

d) Tính diện tích tứ giác AKBE.

Câu 5 (0,5 điểm). Cho hai số thực x, y và x + y = 1. Tính giá trị nhỏ nhất của biểu thức: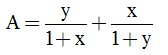  

 

...........................................................................

Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 6

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 6)

Câu 1 (2 điểm). Rút gọn các biểu thức sau:

 

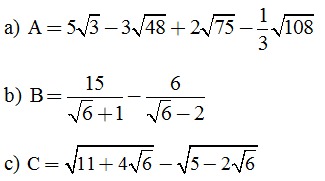
Câu 2 (2,0 điểm). Cho biểu thức : 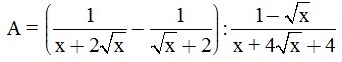 (với x > 0; x ≠ 1)

a)  Rút gọn biểu thức A. 

b)  Tìm x để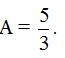  

Câu 3. (0,5 điểm)

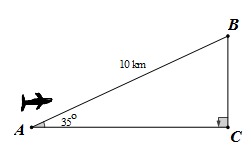
Hình vẽ bên minh họa một chiếc máy bay đang cất cánh từ sân bay. Đường bay lên tạo với phương nằm ngang một góc bằng 35^o. Hỏi sau khi bay được quãng đường 10km thì máy bay ở độ cao bao nhiêu so với mặt đất? (kết quả làm tròn đến số thập phân thứ nhất).

 

Câu 4 (3,5 điểm). Cho tam giác ABC vuông tại A có ∠B = 60^o , BC = 6cm.

a) Tính AB, AC (độ dài làm tròn đến 1 chữ số thập phân).

b) Kẻ đường cao AH của tam giác ABC. Tính HB, HC.

c) Trên tia đối của tia BA lây điểm D sao cho DB = BC. Chứng minh: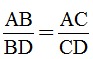  

d) Từ A kẻ đường thẳng song song với phân giác của CBD cắt CD tại K. Chứng minh   .

Câu 5 (0,5 điểm). Giải phương trình:  

 

...........................................................................

Đề thi Giữa học kì 1 Toán lớp 9 Tự luận năm 2022 (7 đề) - Đề 7

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 - Tự luận

Năm học 2022 - 2023

Bài thi môn: Toán lớp 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 7)

Câu 1. (2 điểm): Tính.

 

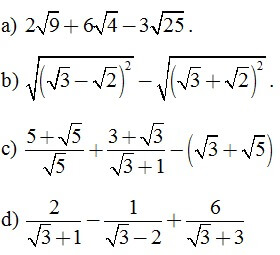
Câu 2. (2 điểm): Giải phương trình

 

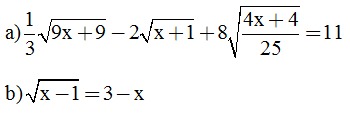
Câu 3. ( 2 điểm): Cho hai biểu thức 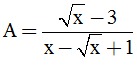 và 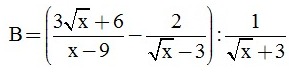 với x ≥ 0; x ≠ 9.

a) Tính giá trị biểu thức A khi x = 4 .

b) Rút gọn biểu thức B.

c) Cho biểu thức P = A.B . Chứng minh  |P| = P với x ≥ 0; x ≠ 9

Câu 4. (3,5 điểm) (Kết quả làm tròn đến số thập phân thứ hai và số đo góc làm tròn đến độ).

1) Một máy bay bay với vận tốc 5m/s lên cao theo phương tạo với đường băng một góc 40^o. Hỏi sau 6 phút máy bay ở độ cao bao nhiêu so với đường băng.

2) Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC tại H, biết BH = 3,6 ; CH = 6,4.

a) Hãy tính độ dài các đoạn thẳng AH, AB và tính số đo góc HCA 

b) Gọi M và N lần lượt là hình chiếu của H lên AB và AC. Chứng minh tam giác AMN đồng dạng với tam giác ACB.

c) Tính diện tích tứ giác  BMNC            

Câu 5. (0,5 điểm): Giải phương trình: