Tài liệu Bộ đề thi Toán lớp 9 Giữa học kì 1 có đáp án năm học 2023 - 2024 gồm 20 đề thi tổng hợp từ đề thi môn Toán 9 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Giữa học kì 1 Toán lớp 9. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi giữa kì 1 Toán 9 bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 1)

Bài 1 (1,5 điểm). Tính giá trị của các biểu thức sau:

  

Bài 2 (2 điểm). Giải các phương trình sau:

Bài 3 (2,5 điểm). Cho biểu thức:

a) Tính giá trị của A khi a = 16

b) Rút gọn biểu thức 

c) So sánh P với 1

Bài 4 (3,5 điểm).

1. (1 điểm)

Một chiếc tivi hình chữ nhật màn hình phẳng 75 inch (đường chéo tivi dài 75 inch) vói góc tạo bởi chiều rộng và đường chéo là 53°08'. Hỏi chiếc ti vi ấy có chiều dài, chiều rộng là bao nhiêu? Biết 1 inch = 2,54cm (kết quả làm tròn đến chữ số thập phân thứ nhất).

2. (2,5 điểm)

Cho tam giác EMF vuông tại M có đường cao MI. Vẽ IP vuông góc với ME (P thuộc ME), IQ vuông góc với MF (Q thuộc MF).

a) Cho biết ME = 4cm, 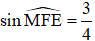. Tính độ dài các đoạn EF, EI, MI.

b) Chứng minh: MP.PE + MQ.QF = MI²

Bài 5 (0,5 điểm).

Tìm giá trị nhỏ nhất của biểu thức 

Đáp án và Hướng dẫn làm bài

Bài 1.

Bài 2.

Phương trình (*) có nghĩa ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 (2)

Kết hợp (1) và (2) suy ra: x = 2 là điều kiện để phương trình có nghĩa.

Thử lại x = 2 vào phương trình ta có:

   (luôn đúng)

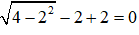
Vậy x = 2 là nghiệm.

Bài 3.

a) Thay a = 16 (tm đkxđ) vào A ta được:

  

Vậy với x = 16 thì A = 5

b) Ta có:

c) So sánh P với 1.

Bài 4.

1.

Màn hình chiếc ti vi là hình chữ nhật ABCD.

Đổi: 75 inch = 190,5cm

Xét tam giác vuông ABD có:

  AD = BD. sin53°08' ≈ 152,4 cm

  AB = BD. cos53°08' ≈ 114,3 cm

2.

Vẽ hình đúng đến câu a)

a) Xét tam giác MEF vuông tại M có:

b) Dùng hệ thức lượng trong tam giác vuông:

+) ΔMIE vuông tại I có: MP.PE = IP²

+) ΔMIF vuông tại I có: MQ.QF = IQ²

+) Xét tứ giác MPIQ có: 

nên tứ giác MPIQ là hình chữ nhật

Suy ra IQ = MP.

Vậy: MP.PE + MQ.QF = IP² + IQ² = IP² + MP² = MI² ( Định lí Pi-ta-go cho tam giác vuông MIP) – đpcm.

Bài 5.

.............................................................................

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 2

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 2)

Bài 1 (2,0 điểm).

1. Thực hiện phép tính.

2. Tìm điều kiện của x để các biểu thức sau có nghĩa:

Bài 2 (2,0 điểm).

1. Phân tích đa thức thành nhân tử.

2. Giải phương trình: 

Bài 3 (2,0 điểm. Cho biểu thức:  

(với x > 0; x ≠ 1)

a. Rút gọn biểu thức A.

b. Tìm x để  

Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a. Tính độ dài các đoạn thẳng AB, AC, AH.

b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.

c. Chứng minh rằng: 

Bài 5 (0,5 điểm).

Cho biểu thức P = x³ + y³ - 3(x + y) + 1993. Tính giá trị biểu thức P với:

Đáp án và Hướng dẫn làm bài

Bài 1.

1. Thực hiện phép tính

2. Tìm điều kiện của x để biểu thức có nghĩa

Bài 2.

1. Phân tích đa thức thành nhân tử:

2. Giải phương trình

⇔ x + 1 = 25 ⇔ x = 24 (thỏa mãn điều kiện xác định)

Vậy phương trình có nghiệm duy nhất x = 24

Bài 3.

a. Rút gọn biểu thức

Bài 4.

a.

Ta có ΔABC vuông tại A, đường cao AH

⇒ AB² = BH.BC = 2.8 = 16 (hệ thức lượng trong tam giác vuông)

⇒  AB = 4cm (Vì AB > 0)

Mà BC² = AB² + AC² (Định lý Pitago trong tam giác vuông ABC)

Có HB + HC = BC ⇒ HC = BC – HB = 8 – 2 = 6 cm

Mà AH² = BH.CH = 2.6 = 12 (hệ thức lượng trong tam giác vuông)

⇒   (Vì AH > 0)

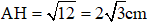
b.

Ta có ΔABK vuông tại A có đường cao AD

⇒ AB² = BD.BK (1)

Mà AB² = BH.BC (chứng minh câu a)  (2)

Từ (1) và (2) suy ra BD.BK = BH.BC

c.

Bài 5.

 

.............................................................................

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 3

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 3)

Bài 1. (2 điểm) Tính giá trị của biểu thức:

Bài 2.(2 điểm) Cho biểu thức:

1. Rút gọn C;

2. Tìm x để .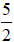

Bài 3.(2 điểm) Giải phương trình

Bài 4.(3,5 điểm) Cho tam giác ABC vuông tại A có đường cao AH. Độ dài BH = 4cm và HC = 6cm.

1. Tính độ dài các đoạn AH, AB, AC.

2. Gọi M là trung điểm của AC. Tính số do góc AMB (làm tròn đến độ).

3. Kẻ AK vuông góc với BM (K ∈ BM). Chứng minh: ΔBKC đồng dạng với ΔBHM.

Bài 5.(0,5 điểm) Cho biểu thức: P = x³ + y³ - 3(x + y) + 2020

Đáp án và Hướng dẫn làm bài

Bài 1.

Bài 2.

Bài 3.

ĐKXĐ: x ≤ -3; x ≥ 3. Vậy nghiệm của phương trình là x = 3 và x = 6.

Bài 4.

1. ΔABC vuông tại A, có đường cao AH.

Áp dụng hệ thức lượng trong tam giác vuông:

2. Do M là trung điểm của AC nên 

Xét ABM vuông tại A:

3. Xét ΔABM vuông tại A, có AK là đường cao

Áp dụng hệ thức lượng trong tam giác vuông

  AB² = BK.BM (1)

ΔABC vuông tại A, có đường cao AH.

Áp dụng hệ thức lượng trong tam giác vuông

  AB² = BH.BC (2)

Từ (1) và (2) ta có:

  

Xét ΔBKC và ΔBHM có:

  

⇒ ΔBKC đồng dạng với ΔBHM (c.g.c) (đpcm)

Bài 5.

.............................................................................

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 4

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 4)

Bài 1 (2,5 điểm). Cho biểu thức:

a) Rút gọn biểu thức

b) Tìm giá trị của x để A = 

Bài 2 (2 điểm). Thực hiện phép tính:

Bài 3 (2 điểm). Giải phương trình:

Bài 4 (3,5 điểm). Cho tam giác ABC có cạnh AB = 12cm, AC = 16cm, BC = 20cm. Kẻ đường cao AM. Kẻ ME vuông góc với AB.

a) Chứng minh tam giác ABC là tam giác vuông.

b) Tính độ dài AM, BM.

c) Chứng minh AE.AB = AC² - MC²

d) Chứng minh AE.AB = MB.MC = EM.AC

Đáp án và Hướng dẫn làm bài

Bài 1.

Bài 2.

Bài 3.

Vậy tập nghiệm của phương trình là S = {2;7}

Bài 4.

a)

Xét tam giác ABC có:

Nên tam giác ABC vuông tại A (theo định lí Pi-ta-go đảo)

b)

+ Xét tam giác ABC vuông tại A (cmt) có AM là đường cao nên:

AM. BC = AB. AC (hệ thức lượng trong tam giác vuông)

+ Lại có: AB² = BM. BC (hệ thức lượng trong tam giác vuông)

c) Xét tam giác AMB vuông tại M có ME là đường cao nên:

AE. AB = AM² (hệ thức lượng trong tam giác vuông) (1)

Xét tam giác AMC vuông tại M có:

d)

+ Xét tam giác ABC vuông tại A có AM là đường cao nên

MB.MC = MA² (hệ thức lượng trong tam giác vuông)

Lại có AE.AB = AM² (cmt)

Do đó AE.AB = AC.EM = MB.MC = AM²

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 5

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 5)

Câu 1 (2 điểm): Tìm $x$ để biểu thức sau xác định:

a) $\sqrt{x-3}$                                                                   

b) $\sqrt{-\frac{2}{2x-1}}$ 

Câu 2 (2 điểm): Thực hiện phép tính:

a) $\sqrt{5}.\sqrt{45}$                                             

b) $\sqrt{12}-\sqrt{27}+\sqrt{3}$                                              

c) $\sqrt{7+2\sqrt{6}}-\sqrt{7-2\sqrt{6}}$  

Câu 3 (2 điểm): Giải phương trình:

a) $\sqrt{3x-2}=6$                                                          

b) $\sqrt{{\left(x-1\right)}^2}=5$  

Câu 4 (3,5 điểm): Cho tam giác $ABC$ vuông tại $A,$ có $AB=12cm,$ $AC=16cm.$ Kẻ đường cao $AM.$ Kẻ $ME\mathrm{\perp }AB.$

a) Tính $BC,\mathrm{\angle }B,\mathrm{\angle }C.$

b) Tính độ dài $AM,BM.$

c) Chứng minh $AE.AB=A{C}^2-M{C}^2.$  

Câu 5 (0,5 điểm):

a) Với $a,b\ge 0.$ Chứng minh $a+b\ge 2\sqrt{ab}.$

b) Áp dụng tính giá trị lớn nhất của biểu thức $S=\sqrt{x-2}+\sqrt{y-3},$ biết $x+y=6.$

Đáp án và Hướng dẫn làm bài

Câu 1

Phương pháp:

Biểu thức $\sqrt{f\left(x\right)}$ xác định $\iff f\left(x\right)\ge 0.$

Cách giải:

a) $\sqrt{x-3}$                                                                  

Biểu thức $\sqrt{x-3}$  xác định $\iff x-3\ge 0$ $\iff x\ge 3.$

Vậy $x\ge 3$ thì biểu thức $\sqrt{x-3}$ xác định.

b) $\sqrt{-\frac{2}{2x-1}}$ 

Biểu thức $\sqrt{-\frac{2}{2x-1}}$ xác định $\iff -\frac{2}{2x-1}\ge 0$ $\iff 2x-1<0$ $\iff x<\frac{1}{2}$

Vậy với $x<\frac{1}{2}$ thì biểu thức $\sqrt{-\frac{2}{2x-1}}$ xác định.

Câu 2

Phương pháp:

Áp dụng các công thức: $\sqrt{A}.\sqrt{B}=\sqrt{AB},A\ge 0,B\ge 0.$

$\sqrt{A^2.B}=\left|A\right|\sqrt{B}=\{\begin{array}{l}A\sqrt{B}khiA\ge 0\\ -A\sqrt{B}khiA<0\end{array},B\ge 0.$

$\sqrt{A^2}=\left|A\right|=\{\begin{array}{l}AkhiA\ge 0\\ -AkhiA<0\end{array}.$

Cách giải:

a) $\sqrt{5}.\sqrt{45}$                                             

Ta có: $\sqrt{5}.\sqrt{45}=\sqrt{5.45}=\sqrt{\mathrm{5.5.9}}$ $=\sqrt{5^2{.3}^2}=5.3=15.$

b) $\sqrt{12}-\sqrt{27}+\sqrt{3}$                      

Ta có:

$\begin{array}{l}\sqrt{12}-\sqrt{27}+\sqrt{3}\\ =\sqrt{2^2.3}-\sqrt{3^2.3}+\sqrt{3}\\ =2\sqrt{3}-3\sqrt{3}+\sqrt{3}=0.\end{array}$

 c) $\sqrt{7+2\sqrt{6}}-\sqrt{7-2\sqrt{6}}$  

Ta có:

$\begin{array}{l}\sqrt{7+2\sqrt{6}}-\sqrt{7-2\sqrt{6}}\\ =\sqrt{{\left(\sqrt{6}\right)}^2+2\sqrt{6}+1}-\sqrt{{\left(\sqrt{6}\right)}^2-2\sqrt{6}+1}\\ =\sqrt{{\left(\sqrt{6}+1\right)}^2}-\sqrt{{\left(\sqrt{6}-1\right)}^2}\\ =\left|\sqrt{6}+1\right|-\left|\sqrt{6}-1\right|\\ =\sqrt{6}+1-\left(\sqrt{6}-1\right)\left(do\sqrt{6}-2>0\right)\\ =\sqrt{6}+1-\sqrt{6}+1\\ =2.\end{array}$

Câu 3

Phương pháp:

Giải phương trình: $\sqrt{f\left(x\right)}=a\left(a\ge 0\right)$ $\iff \{\begin{array}{l}f\left(x\right)\ge 0\\ f\left(x\right)=a^2\end{array}.$

$\sqrt{{\left[f\left(x\right)\right]}^2}=a\left(a\ge 0\right)$ $\iff \left|f\left(x\right)\right|=a$ $\iff [\begin{array}{l}f\left(x\right)=a\\ f\left(x\right)=-a\end{array}.$

Cách giải:

Giải phương trình:

a) $\sqrt{3x-2}=6$          

Điều kiện: $3x-2\ge 0$ $\iff x\ge \frac{2}{3}$

Khi đó ta có phương trình $\iff 3x-2=6^2$

$\begin{array}{l}\iff 3x-2=36\\ \iff 3x=38\\ \iff x=\frac{38}{3}\left(tm\right)\end{array}$

Vậy phương trình có nghiệm duy nhất $x=\frac{38}{3}.$                                              

b) $\sqrt{{\left(x-1\right)}^2}=5$  

Điều kiện: $x\in \mathbb{R}.$

$\begin{array}{l}\sqrt{{\left(x-1\right)}^2}=5\\ \iff \left|x-1\right|=5\\ \iff [\begin{array}{l}x-1=5\\ x-1=-5\end{array}\iff [\begin{array}{l}x=6\\ x=-4\end{array}\end{array}$

Vậy phương trình có tập nghiệm: $S=\left\{-4;6\right\}.$

Câu 4

Phương pháp:

a) Sử dụng định lý Pitago để tính $BC=\sqrt{A{B}^2+A{C}^2}.$

Sử dụng các công thức về tỉ số lượng giác của góc nhọn trong tam giác vuông và định lý tổng số đo của 3 góc trong tam giác để tính số đo của $\mathrm{\angle }B,\mathrm{\angle }C.$

b) Áp dụng hệ thức lượng trong tam giác $ABC$ vuông tại $A,$ có đường cao $AM$  ta có: $AM.BC=AB.AC$ và $A{B}^2=BM.BC.$  

c) Áp dụng hệ thức lượng trong tam giác $AMB$ vuông tại $A,$ có đường cao $ME$  ta có: $A{M}^2=AE.AB$ và định lý Pitago cho $\mathrm{\Delta }AMC$ vuông tại $M$ để chứng minh đẳng thức đề bài yêu cầu.

Cách giải:

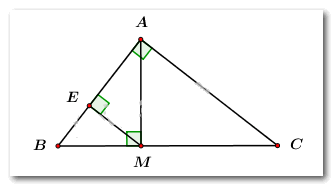
a) Tính $BC,\mathrm{\angle }B,\mathrm{\angle }C.$

Áp dụng định lý Pitago cho $\mathrm{\Delta }ABC$ vuông tại $A$ ta có:

$BC=\sqrt{A{B}^2+A{C}^2}$ $=\sqrt{{12}^2+{16}^2}=\sqrt{400}$ $=20cm.$

Xét $\mathrm{\Delta }ABC$ vuông tại $A$ ta có:

$\sin \mathrm{\angle }B=\frac{AC}{AB}=\frac{16}{20}=0,8$ $\Rightarrow \mathrm{\angle }B\approx {53}^0.$

$\Rightarrow \mathrm{\angle }C={90}^0-\mathrm{\angle }B$ $={90}^0-{53}^0={37}^0.$

b) Tính độ dài $AM,BM.$

Áp dụng hệ thức lượng trong tam giác $ABC$ vuông tại $A,$ có đường cao $AM$  ta có: $AM.BC=AB.AC$

$\Rightarrow AM=\frac{AB.AC}{BC}=\frac{12.16}{20}=9.6\left(cm\right).$

Lại có: $A{B}^2=BM.BC$ $\Rightarrow BM=\frac{A{B}^2}{BC}=\frac{{12}^2}{20}=7,2cm.$

Vậy $AM=9,6cm$ và $BM=7,2cm.$

c) Chứng minh $AE.AB=A{C}^2-M{C}^2.$ 

Áp dụng hệ thức lượng trong tam giác $AMB$ vuông tại $A,$ có đường cao $ME$  ta có: $A{M}^2=AE.AB$

Áp dụng định lý Pitago cho $\mathrm{\Delta }AMC$ vuông tại $M$ ta có: $A{M}^2=A{C}^2-M{C}^2$

$\Rightarrow AE.AB=A{C}^2-M{C}^2\left(=A{M}^2\right)\left(dpcm\right).$

Câu 5

Phương pháp:

a) Áp dụng hằng đẳng thức: ${\left(\sqrt{a}-\sqrt{b}\right)}^2\ge 0\mathrm{\forall }a,b\ge 0.$  

b) Áp dụng bất đẳng thức $a+b\ge 2\sqrt{ab}$ khi $a,b\ge 0$ để tìm GTLN của biểu thức.

Cách giải:

a) Với $a,b\ge 0.$ Chứng minh $a+b\ge 2\sqrt{ab}.$

Với mọi $a,b\ge 0$ ta có: ${\left(\sqrt{a}-\sqrt{b}\right)}^2\ge 0$

$\iff a-2\sqrt{ab}+b\ge 0$ $\iff a+b\ge 2\sqrt{ab}\left(dpcm\right).$

Dấu “=” xảy ra $\iff a=b.$

b) Áp dụng tính giá trị lớn nhất của biểu thức $S=\sqrt{x-2}+\sqrt{y-3},$ biết $x+y=6.$

Điều kiện: $x\ge 2,y\ge 3.$

Ta có: $S=\sqrt{x-2}+\sqrt{y-3}$

$$\begin{array}{l}\Rightarrow S^2=x-2+y-3+2\sqrt{\left(x-2\right)\left(y-3\right)}\\ =x+y-5+2\sqrt{\left(x-2\right)\left(y-3\right)}\\ =6-5+2\sqrt{\left(x-2\right)\left(y-3\right)}\\ =1+2\sqrt{\left(x-2\right)\left(y-3\right)}.\end{array}$$

Áp dụng bất đẳng thức $a+b\ge 2\sqrt{ab}$ với $a,b\ge 0$ ta có:

$2\sqrt{\left(x-2\right)\left(y-3\right)}\le x-2+y-3=6-5=1$

$\Rightarrow S^2=1+2\sqrt{\left(x-2\right)\left(y-3\right)}\le 1+1=2$

$\Rightarrow S^2\le 2\Rightarrow S\le \sqrt{2}.$

Dấu “=” xảy ra $\iff \{\begin{array}{l}x-2=y-3\\ x+y=6\end{array}$ $\iff \{\begin{array}{l}x-y=-1\\ x+y=6\end{array}$ $\iff \{\begin{array}{l}x=\frac{5}{2}\left(tm\right)\\ y=\frac{7}{2}\left(tm\right)\end{array}$

Vậy giá trị lớn nhất của $S=\sqrt{2}$ khi $\left(x;y\right)=\left(\frac{5}{2};\frac{7}{2}\right).$

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 6

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 6)

Câu 1 (2 điểm): Thực hiện phép tính:

a) $5\sqrt{12}-\sqrt{27}-2\sqrt{75}+\sqrt{48}$                                                     

b) $\frac{2}{\sqrt{13}-\sqrt{11}}+\frac{5}{4+\sqrt{11}}-\sqrt{52}$

c) $\sqrt{6+2\sqrt{5}}+\sqrt{9-4\sqrt{5}}-\sqrt{20}$

Câu 2 (2 điểm): Giải các phương trình sau:

a) $3\sqrt{x}=\sqrt{16x}-5$                     

b) $\sqrt{4x-8}-\sqrt{9x-18}+4\sqrt{\frac{x-2}{25}}=-3$                   

c) $x-\sqrt{5x+4}=2$

Câu 3 (2 điểm): Cho biểu thức: $A=\frac{\sqrt{x}-2}{\sqrt{x}+1};$ $B=\frac{\sqrt{x}}{\sqrt{x}+1}-\frac{\sqrt{x}-4}{1-x}\left(x\ge 0,x\ne 1\right).$

a) Tính giá trị của biểu thức $A$ khi $x=25.$

b) Rút gọn biểu thức $B.$

c) Tìm $x$để $A:B<\frac{1}{2}.$  

Câu 4 (3 điểm): Cho $\mathrm{\Delta }ABC$ vuông tại $A,$ đường cao $AH,$ $AB=6cm,$ $BC=10cm.$

a) Giải tam giác vuông $ABC.$ (kết quả làm tròn đến phút)

b) Kẻ tia phân giác góc $A$ cắt $BC$ tại $E.$ Tính $BE,AE.$

c) Gọi $M,N$ theo thứ tự là hình chiếu của $E$ trên $AB$ và $AC.$ Tính diện tích tứ giác $AMEN.$  

Câu 5 (1 điểm):

a) Giải bài toán sau: (kết quả làm tròn đến số thập phân thứ hai)

Để đo chiều rộng của một khúc sông $AH,$ người ta chọn hai vị trí $B,C$ cùng một bờ. Biết $BC=60m,$ $\mathrm{\angle }ACB={38}^0,$ $\mathrm{\angle }ABC={30}^0.$  Hãy tính chiều rộng $AH$ của khúc sông đó.

 

b) Tính giá trị nhỏ nhất của biểu thức $A=\sqrt{{\left(x-2019\right)}^2}+\sqrt{{\left(x-2020\right)}^2}.$  

Đáp án và Hướng dẫn làm bài

Câu 1

Phương pháp:

a) Sử dụng công thức: $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}=\{\begin{array}{l}A\sqrt{B}khiA\ge 0\\ -A\sqrt{B}khiA<0\end{array},B\ge 0.$

b) Sử dụng công thức trục căn thức ở mẫu: $\frac{1}{\sqrt{A}-\sqrt{B}}=\frac{\sqrt{A}+\sqrt{B}}{A-B}\left(A\ge 0,B\ge 0,A\ne B\right)$ và $\frac{1}{A+\sqrt{B}}=\frac{A-\sqrt{B}}{A^2-B}$ với $B\ge 0,A^2\ne B.$  

c) Sử dụng công thức hằng đẳng thức ở mẫu: $\sqrt{A^2}=\left|A\right|=\{\begin{array}{l}AkhiA\ge 0\\ -AkhiA<0\end{array}.$

Cách giải:

Thực hiện phép tính:

a) $5\sqrt{12}-\sqrt{27}-2\sqrt{75}+\sqrt{48}$                 

$\begin{array}{l}=5\sqrt{{3.2}^2}-\sqrt{3^2.3}-2\sqrt{5^2.3}+\sqrt{4^2.3}\\ =5.2\sqrt{3}-3\sqrt{3}-2.5\sqrt{3}+4\sqrt{3}\\ =10\sqrt{3}-3\sqrt{3}-10\sqrt{3}+4\sqrt{3}\\ =\sqrt{3}.\end{array}$                                 

b) $\frac{2}{\sqrt{13}-\sqrt{11}}+\frac{5}{4+\sqrt{11}}-\sqrt{52}$

$\begin{array}{l}=\frac{2\left(\sqrt{13}+\sqrt{11}\right)}{13-11}+\frac{5\left(4-\sqrt{11}\right)}{4^2-11}-\sqrt{2^2.13}\\ =\frac{2\left(\sqrt{13}+\sqrt{11}\right)}{2}+\frac{5\left(4-\sqrt{11}\right)}{5}-\sqrt{2^2.13}\\ =\sqrt{13}+\sqrt{11}+4-\sqrt{11}-2\sqrt{13}\\ =4-\sqrt{13}.\end{array}$

c) $\sqrt{6+2\sqrt{5}}+\sqrt{9-4\sqrt{5}}-\sqrt{20}$

$\begin{array}{l}=\sqrt{{\left(\sqrt{5}\right)}^2+2\sqrt{5}+1}+\sqrt{{\left(\sqrt{5}\right)}^2-\mathrm{2.2.}\sqrt{5}+2^2}-\sqrt{2^2.5}\\ =\sqrt{{\left(\sqrt{5}+1\right)}^2}+\sqrt{{\left(\sqrt{5}-2\right)}^2}-2\sqrt{5}\\ =\left|\sqrt{5}+1\right|+\left|\sqrt{5}-2\right|-2\sqrt{5}\\ =\sqrt{5}+1+\sqrt{5}-2-2\sqrt{5}\left(do\sqrt{5}-2>0\right)\\ =-1.\end{array}$

Câu 2

Phương pháp:

Tìm điều kiện để phương trình xác định.

Giải phương trình: $\sqrt{f\left(x\right)}=a\left(a\ge 0\right)$ $\iff f^2\left(x\right)=a^2.$

Cách giải:

Giải các phương trình sau:

a) $3\sqrt{x}=\sqrt{16x}-5(\ast )$  

Điều kiện: $x\ge 0$

$\begin{array}{l}\Rightarrow (\ast )\iff 3\sqrt{x}=4\sqrt{x}-5\\ \iff \sqrt{x}=5\iff x=25\left(tm\right)\end{array}$

Vậy phương trình có nghiệm $x=25.$        

b) $\sqrt{4x-8}-\sqrt{9x-18}+4\sqrt{\frac{x-2}{25}}=-3(\ast )$       

Điều kiện:$x\ge 2.$  

$\begin{array}{l}\Rightarrow (\ast )\iff \sqrt{4\left(x-2\right)}-\sqrt{9\left(x-2\right)}+4.\frac{\sqrt{x-2}}{\sqrt{25}}=-3\\ \iff 2\sqrt{x-2}-3\sqrt{x-2}+\frac{4}{5}\sqrt{x-2}=-3\\ \iff -\frac{1}{5}.\sqrt{x-2}=-3\\ \iff \sqrt{x-2}=15\\ \iff x-2=225\\ \iff x=227\left(tm\right)\end{array}$

Vậy phương trình có nghiệm $x=227.$

c) $x-\sqrt{5x+4}=2(\ast )$

Điều kiện: $$x\ge -\frac{4}{5}.$$

$\begin{array}{l}\Rightarrow (\ast )\iff x-2=\sqrt{5x+4}\\ \iff \{\begin{array}{l}x-2\ge 0\\ {\left(x-2\right)}^2=5x+4\end{array}\iff \{\begin{array}{l}x\ge 2\\ x^2-4x+4=5x+4\end{array}\\ \iff \{\begin{array}{l}x\ge 2\\ x^2-9x=0\end{array}\iff \{\begin{array}{l}x\ge 2\\ x\left(x-9\right)=0\end{array}\\ \iff \{\begin{array}{l}x\ge 2\\ [\begin{array}{l}x=0\\ x-9=0\end{array}\end{array}\iff \{\begin{array}{l}x\ge 2\\ [\begin{array}{l}x=0\\ x=9\end{array}\end{array}\iff x=9.\end{array}$

Vậy phương trình có nghiệm $x=9.$

Câu 3

Phương pháp:

a) Thay giá trị $x=25\left(tm\right)$ vào biểu thức $A$ để tính giá trị của biểu thức.

b) Biến đổi, quy đồng sau đó rút gọn biểu thức đã cho.

c) Giải bất phương trình $A:B<\frac{1}{2}$ để tìm $x.$ Đối chiếu với điều kiện xác định rồi kết luận.

Cách giải:

Cho biểu thức: $A=\frac{\sqrt{x}-2}{\sqrt{x}+1};$ $B=\frac{\sqrt{x}}{\sqrt{x}+1}-\frac{\sqrt{x}-4}{1-x}\left(x\ge 0,x\ne 1\right).$

a) Tính giá trị của biểu thức $A$ khi $x=25.$

Điều kiện: $x\ge 0,x\ne 1.$

Thay giá trị $x=25\left(tm\right)$ vào biểu thức ta được: $A=\frac{\sqrt{25}-2}{\sqrt{25}+1}=\frac{5-2}{5+1}=\frac{1}{2}.$

Vậy với $x=25$ thì $A=\frac{1}{2}.$

b) Rút gọn biểu thức $B.$

Điều kiện: $x\ge 0,x\ne 1.$

$\begin{array}{l}B=\frac{\sqrt{x}}{\sqrt{x}+1}-\frac{\sqrt{x}-4}{1-x}=\frac{\sqrt{x}}{\sqrt{x}+1}+\frac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\frac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\frac{x-\sqrt{x}+\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\frac{x-4}{x-1}.\end{array}$

c) Tìm $x$để $A:B<\frac{1}{2}.$  

Điều kiện: $x\ge 0,x\ne 1.$

Ta có: $A:B<\frac{1}{2}$

$\begin{array}{l}\iff \frac{\sqrt{x}-2}{\sqrt{x}+1}:\frac{x-4}{x-1}<\frac{1}{2}\\ \iff \frac{\sqrt{x}-2}{\sqrt{x}+1}.\frac{x-1}{x-4}<\frac{1}{2}\\ \iff \frac{\sqrt{x}-2}{\sqrt{x}+1}.\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}<\frac{1}{2}\\ \iff \frac{\sqrt{x}-1}{\sqrt{x}+2}-\frac{1}{2}<0\\ \iff \frac{2\sqrt{x}-2-\sqrt{x}-2}{2\left(\sqrt{x}+2\right)}<0\\ \iff \sqrt{x}-4<0\left(do2\left(\sqrt{x}+2\right)>0\mathrm{\forall }xtmdkxd\right)\\ \iff \sqrt{x}<4\\ \iff x<16\end{array}$ 

Kết hợp với điều kiện $x\ge 0,x\ne 1$ ta có: $0\le x<16,x\ne 1$ thỏa mãn bài toán.

Vậy $0\le x<16,x\ne 1$ thỏa mãn bài toán.

Câu 4

Phương pháp:

a) Sử dụng định lý Pitago và tỉ số lượng giác của góc nhọn trong tam giác để giải $\mathrm{\Delta }ABC.$

b) Sử dụng tính chất tia phân giác của tam giác để tính $BE,AE.$

Ta có: $AE$ là tia phân giác của $\mathrm{\angle }A$ $\Rightarrow \frac{BE}{BA}=\frac{CE}{CA}.$  

c) Chứng minh tứ giác $AMEN$ là hình chữ nhật.

Vì $AE$ là phân giác của $\mathrm{\angle }A$ $\Rightarrow \mathrm{\angle }MAE=\mathrm{\angle }NEA={45}^0$

$\Rightarrow \mathrm{\Delta }AME,\mathrm{\Delta }ANE$ là các tam giác vuông cân tị $M$ và $N.$

$\Rightarrow AMEN$ là hình vuông.

Từ đó tính $AM,AN$ $\Rightarrow S_{AMEN}=A{M}^2.$

Cách giải:

Cho $\mathrm{\Delta }ABC$ vuông tại $A,$ đường cao $AH,$ $AB=6cm,$ $BC=10cm.$

a) Giải tam giác vuông $ABC.$ (kết quả làm tròn đến phút)

Áp dụng định lý Pitago cho $\mathrm{\Delta }ABC$ vuông tại $A$ ta có:

$AC=\sqrt{B{C}^2-A{B}^2}=\sqrt{{10}^2-6^2}=8cm.$

Xét $\mathrm{\Delta }ABC$ vuông tại $A$ ta có:

$\sin \mathrm{\angle }B=\frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$ $\Rightarrow \mathrm{\angle }B\approx {53}^0{8}^{\prime }$

$\sin \mathrm{\angle }C=\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}$ $\Rightarrow \mathrm{\angle }C\approx {36}^0{52}^{\prime }$

Vậy $AC=8cm,\mathrm{\angle }B\approx {53}^0{8}^{\prime },\mathrm{\angle }C\approx {36}^0{52}^{\prime }.$

b) Kẻ tia phân giác góc $A$ cắt $BC$ tại $E.$ Tính $BE,AE.$

Áp dụng tính chất của tia phân giác ta có: $\frac{BE}{BA}=\frac{CE}{CA}\iff \frac{BE}{6}=\frac{CE}{8}$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\begin{array}{l}\frac{BE}{6}=\frac{CE}{8}=\frac{BE+CE}{6+8}=\frac{10}{14}=\frac{5}{7}\\ \Rightarrow \{\begin{array}{l}BE=\frac{5}{7}.6=\frac{30}{7}cm\\ CE=\frac{5}{7}.8=\frac{40}{7}cm\end{array}.\end{array}$

Áp dụng hệ thức lượng trong $\mathrm{\Delta }ABC$ vuông tại$A,$ có đường cao $AH$ ta có:

$AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8cm.$

$A{B}^2=BH.BC$ $\Rightarrow BH=\frac{A{B}^2}{BC}=\frac{6^2}{10}=3,6cm.$

$\Rightarrow HE=BE-BH=\frac{30}{7}-3,6=\frac{24}{35}.$

Áp dụng định lý Pitago cho  $\mathrm{\Delta }AHE$ vuông tại $H$ ta có:

$AE=\sqrt{A{H}^2+H{E}^2}=\sqrt{4,8^2+{\left(\frac{24}{35}\right)}^2}$ $=\sqrt{\frac{1152}{49}}=\frac{24\sqrt{2}}{7}cm.$

Vậy $BE=\frac{30}{7}cm,AE=\frac{24\sqrt{2}}{7}cm.$

c) Gọi $M,N$ theo thứ tự là hình chiếu của $E$ trên $AB$ và $AC.$ Tính diện tích tứ giác $AMEN.$  

Ta có: $\{\begin{array}{l}EM\mathrm{\perp }AB=\left\{M\right\}\\ EN\mathrm{\perp }AC=\left\{N\right\}\end{array}$ $\Rightarrow \mathrm{\angle }AME=\mathrm{\angle }ANE={90}^0$

Xét tứ giác $AMEN$ ta có:$\mathrm{\angle }MAN=\mathrm{\angle }AME=\mathrm{\angle }ANE={90}^0$

$\Rightarrow AMEN$ là hình chữ nhật.

Vì $AE$ là phân giác của $\mathrm{\angle }A$ $\Rightarrow \mathrm{\angle }MAE=\mathrm{\angle }NEA={45}^0$

$\Rightarrow \mathrm{\Delta }AME,\mathrm{\Delta }ANE$ là các tam giác vuông cân tị $M$ và $N.$

$\Rightarrow AMEN$ là hình vuông.

Xét $\mathrm{\Delta }AME$ vuông cân tại$M$ ta có:

$\begin{array}{l}A{E}^2=A{M}^2+M{E}^2=2A{M}^2\\ \Rightarrow A{M}^2=\frac{A{E}^2}{2}=\frac{1152}{2.49}=\frac{576}{49}\\ \Rightarrow S_{AMEN}=A{M}^2=\frac{576}{49}c{m}^2.\end{array}$

Câu 5

Phương pháp:

a) Áp dụng hệ số về cạnh và góc trong các tam giác $ABH,ACH$ vuông tại $H$ để tính $AH.$

b) Sử dụng bất đẳng thức trị tuyệt đối: $\left|a\right|+\left|b\right|\ge \left|a+b\right|.$

Dấu “=” xảy ra $ab\ge 0.$

Cách giải:

a) Giải bài toán sau: (kết quả làm tròn đến số thập phân thứ hai)

Để đo chiều rộng của một khúc sông $AH,$ người ta chọn hai vị trí $B,C$ cùng một bờ. Biết $BC=60m,$ $\mathrm{\angle }ACB={38}^0,$ $\mathrm{\angle }ABC={30}^0.$  Hãy tính chiều rộng $AH$ của khúc sông đó.

Xét $\mathrm{\Delta }ABH$ vuông tại $H$ ta có:  

Xét $\mathrm{\Delta }ACH$ vuông tại $H$ ta có: $CH=AH\cot C=AH\cot {38}^0\approx 1,28AH$

$\begin{array}{l}\Rightarrow BC=BH+HC=\sqrt{3}AH+1,28AH\\ \iff 60=3,01AH\\ \iff AH\approx 19,92m.\end{array}$

Vậy chiều rộng của khúc sông khoảng $19,92m.$

b) Tính giá trị nhỏ nhất của biểu thức $A=\sqrt{{\left(x-2019\right)}^2}+\sqrt{{\left(x-2020\right)}^2}.$  

Ta có:

$\begin{array}{l}A=\sqrt{{\left(x-2019\right)}^2}+\sqrt{{\left(x-2020\right)}^2}\\ =\left|x-2019\right|+\left|x-2020\right|\\ =\left|x-2019\right|+\left|2020-x\right|\\ \ge \left|x-2019+2020-x\right|=1\end{array}$

Dấu “=” xảy ra $\iff \left(x-2019\right)\left(2020-x\right)\ge 0$

$\begin{array}{l}\iff \left(x-2019\right)\left(x-2020\right)\le 0\\ \iff 2019\le x\le 2020.\end{array}$

Vậy $MinA=1$ khi $2019\le x\le 2020.$

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 7

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 7)

Bài 1 (2 điểm):

Tính:

a) $A=\sqrt{3}\left(\sqrt{12}-\sqrt{27}+5\right)-\sqrt{75}$                                         

b) $B=2\sqrt{45}+\sqrt{{\left(1-\sqrt{5}\right)}^2}-\frac{8}{\sqrt{5}+1}$  

Bài 2 (2 điểm):

Giải các phương trình sau:

a) $\frac{1}{2}\sqrt{x-2}-\sqrt{4x-8}+\sqrt{9x-18}-5=0$                                

b) $\sqrt{x^2-4x+4}=2x-1$  

Bài 3 (2 điểm):

Cho hai biểu thức $A=\frac{\sqrt{x}}{\sqrt{x}-2}$ và $B=\frac{2\sqrt{x}}{\sqrt{x}-3}-\frac{x+9\sqrt{x}}{x-9}$ với $x>0,x\ne 4,x\ne 9.$

a) Tính giá trị của biểu thức $A$ khi $x=100.$

b) Rút gọn biểu thức $B.$

c) Tìm giá trị nguyên của $x$ để biểu thức $M=A:B$ có giá trị nguyên.

Bài 4 (4 điểm):

Cho $\mathrm{\Delta }ABC$ vuông tại $A\left(AB<AC\right),$ đường cao $AH,$ trung tuyến $AM.$ Gọi $D,E$ thứ tự là hình chiếu của $H$ trên $AB,AC;$ $K$ là giao điểm của $AM$ và $DE.$

a) Chứng minh $AD.AB=AE.AC.$

b) Chứng minh $AM\mathrm{\perp }DE$ và $A{H}^3=DK.A{B}^2.$

c) Biết $HB=3cm,HC=7cm.$ Tính $AB,AC,DE$ và $\sqrt[3]{B{D}^2}+\sqrt[3]{C{E}^2}.$

Đáp án và Hướng dẫn làm bài

Bài 1

Phương pháp:

a) Sử dụng công thức: $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}=\{\begin{array}{l}A\sqrt{B}khiA\ge 0\\ -A\sqrt{B}khiA<0\end{array},B\ge 0.$

b) Sử dụng công thức trục căn thức ở mẫu: $\frac{1}{\sqrt{A}-\sqrt{B}}=\frac{\sqrt{A}+\sqrt{B}}{A-B}\left(A\ge 0,B\ge 0,A\ne B\right)$ và $\frac{1}{A+\sqrt{B}}=\frac{A-\sqrt{B}}{A^2-B}$ với $B\ge 0,A^2\ne B.$ 

+) Sử dụng công thức hằng đẳng thức ở mẫu: $\sqrt{A^2}=\left|A\right|=\{\begin{array}{l}AkhiA\ge 0\\ -AkhiA<0\end{array}.$

Cách giải:

a) $A=\sqrt{3}\left(\sqrt{12}-\sqrt{27}+5\right)-\sqrt{75}$                                         

$\begin{array}{l}A=\sqrt{3}\left(\sqrt{12}-\sqrt{27}+5\right)-\sqrt{75}\\ =\sqrt{3}\left(\sqrt{2^2.3}-\sqrt{3^2.3}+5\right)-\sqrt{5^2.3}\\ =\sqrt{3}\left(2\sqrt{3}-3\sqrt{3}+5\right)-5\sqrt{3}\\ =\sqrt{3}\left(5-\sqrt{3}\right)-5\sqrt{3}\\ =5\sqrt{3}-3-5\sqrt{3}\\ =-3.\end{array}$

b) $B=2\sqrt{45}+\sqrt{{\left(1-\sqrt{5}\right)}^2}-\frac{8}{\sqrt{5}+1}$  

$\begin{array}{l}B=2\sqrt{45}+\sqrt{{\left(1-\sqrt{5}\right)}^2}-\frac{8}{\sqrt{5}+1}\\ =2\sqrt{3^2.5}+\left|1-\sqrt{5}\right|-\frac{8\left(\sqrt{5}-1\right)}{5-1}\\ =2.3\sqrt{5}+\sqrt{5}-1-\frac{8\left(\sqrt{5}-1\right)}{4}\left(do1-\sqrt{5}<0\right)\\ =6\sqrt{5}+\sqrt{5}-1-2\left(\sqrt{5}-1\right)\\ =7\sqrt{5}-1-2\sqrt{5}+2\\ =5\sqrt{5}+1.\end{array}$

Bài 2

Phương pháp:

Tìm điều kiện để phương trình xác định.

Giải phương trình: $\sqrt{f\left(x\right)}=a\left(a\ge 0\right)$ $\iff f^2\left(x\right)=a^2.$

$\sqrt{f^2\left(x\right)}=g\left(x\right)\iff \{\begin{array}{l}g\left(x\right)\ge 0\\ \left|f\left(x\right)\right|=g\left(x\right)\end{array}$  

Cách giải:

a) $\frac{1}{2}\sqrt{x-2}-\sqrt{4x-8}+\sqrt{9x-18}-5=0$                               

Điều kiện: $x\ge 2.$

$\begin{array}{l}\frac{1}{2}\sqrt{x-2}-\sqrt{4x-8}+\sqrt{9x-18}-5=0\\ \iff \frac{1}{2}\sqrt{x-2}-\sqrt{4\left(x-2\right)}+\sqrt{9\left(x-2\right)}-5=0\\ \iff \frac{1}{2}\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=5\\ \iff \frac{3}{2}\sqrt{x-2}=5\\ \iff \sqrt{x-2}=\frac{10}{3}\\ \iff x-2=\frac{100}{9}\\ \iff x=\frac{118}{9}\left(tm\right)\end{array}$

Vậy phương trình có nghiệm duy nhất $x=\frac{118}{9}.$

b) $\sqrt{x^2-4x+4}=2x-1$

$\begin{array}{l}\iff \{\begin{array}{l}2x-1\ge 0\\ \sqrt{{\left(x-2\right)}^2}=2x-1\end{array}\iff \{\begin{array}{l}x\ge \frac{1}{2}\\ \left|x-2\right|=2x-1\end{array}\\ \iff \{\begin{array}{l}x\ge \frac{1}{2}\\ [\begin{array}{l}x-2=2x-1\\ x-2=-2x+1\end{array}\end{array}\iff \{\begin{array}{l}x\ge \frac{1}{2}\\ [\begin{array}{l}x=-1\\ x=1\end{array}\end{array}\iff x=1.\end{array}$

Vậy phương trình có nghiệm duy nhất $x=1.$  

Bài 3

Phương pháp:

a) Thay giá trị $x=100\left(tm\right)$ vào biểu thức $A$ để tính giá trị của biểu thức.

b) Biến đổi, quy đồng sau đó rút gọn biểu thức đã cho.

c) Tính biểu thức $M=A:B.$

Biến đổi $M=a+\frac{b}{MS},a,b\in \mathbb{Z}$ $\Rightarrow M\in \mathbb{Z}\iff b⋮MS$ hay $MS\in U\left(b\right).$

Từ đó ta lập bảng giá trị để tìm $x.$ Đối chiếu với điều kiện của $x$ rồi kết luận.

Cách giải:

Cho hai biểu thức $A=\frac{\sqrt{x}}{\sqrt{x}-2}$ và $B=\frac{2\sqrt{x}}{\sqrt{x}-3}-\frac{x+9\sqrt{x}}{x-9}$ với $x>0,x\ne 4,x\ne 9.$

a) Tính giá trị của biểu thức $A$ khi $x=100.$

Điều kiện: $x>0,x\ne 4,x\ne 9.$

Thay $x=100\left(tm\right)$ vào biểu thức $A$ ta có:  

Vậy với  thì  

b) Rút gọn biểu thức  

Điều kiện: $A=\frac{\sqrt{100}}{\sqrt{100}-2}$

$\begin{array}{l}B=\frac{2\sqrt{x}}{\sqrt{x}-3}-\frac{x+9\sqrt{x}}{x-9}\\ =\frac{2\sqrt{x}}{\sqrt{x}-3}-\frac{x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\frac{2\sqrt{x}\left(\sqrt{x}+3\right)-x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\frac{2x+6\sqrt{x}-x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\frac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\frac{\sqrt{x}}{\sqrt{x}+3}\end{array}$

c) Tìm giá trị nguyên của $x$ để biểu thức $M=A:B$ có giá trị nguyên.

Điều kiện: $x>0,x\ne 4,x\ne 9.$

Ta có: $M=A:B=\frac{\sqrt{x}}{\sqrt{x}-2}:\frac{\sqrt{x}}{\sqrt{x}+3}$

$\begin{array}{l}\Rightarrow M=\frac{\sqrt{x}}{\sqrt{x}-2}.\frac{\sqrt{x}+3}{\sqrt{x}}=\frac{\sqrt{x}+3}{\sqrt{x}-2}\\ =\frac{\sqrt{x}-2+5}{\sqrt{x}-2}=1+\frac{5}{\sqrt{x}-2}\end{array}$

$\Rightarrow M\in \mathbb{Z}\iff \frac{5}{\sqrt{x}-2}\in \mathbb{Z}$

$\iff 5⋮\left(\sqrt{x}-2\right)$ hay $\left(\sqrt{x}-2\right)\in U\left(5\right)$

Mà $U\left(5\right)=\left\{\pm 1;\pm 5\right\}$ $\Rightarrow \left(\sqrt{x}-2\right)\in \left\{\pm 1;\pm 5\right\}$

Ta có bảng giá trị:

Vậy $x\in \left\{1;49\right\}$ thì $M=A:B$ đạt giá trị nguyên.

Bài 4

Phương pháp:

a) Sử dụng hệ thức lượng trong tam giác vuông để chứng minh đẳng thức.

b) Chứng minh các cặp tam giác đồng dạng tương ứng rồi suy ra $AM\mathrm{\perp }DE.$

Sử dụng hệ thức lượng trong tam giác vuông để chứng minh đẳng thức cần chứng minh.

c) Sử dụng hệ thức lượng để tính các cạnh bài toán yêu cầu.

Cách giải:

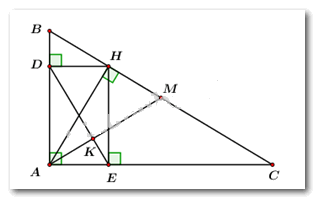
a) Chứng minh $AD.AB=AE.AC.$

Ta có: $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB,AC$

$\{\begin{array}{l}HD\mathrm{\perp }AB=\left\{D\right\}\\ HE\mathrm{\perp }AC=\left\{E\right\}\end{array}$ $\Rightarrow \mathrm{\angle }BDH=\mathrm{\angle }HEC={90}^0$

Áp dụng hệ thức lượng trong $\mathrm{\Delta }ABH$ vuông tại $H,$ có đường cao $HD$ ta có: $A{H}^2=AD.AB$

Áp dụng hệ thức lượng trong $\mathrm{\Delta }ACH$ vuông tại $H,$ có đường cao $HE$ ta có: $A{H}^2=AE.AC$

$\Rightarrow AD.AB=AE.AC\left(=A{H}^2\right)\left(dpcm\right).$

b) Chứng minh $AM\mathrm{\perp }DE$ và $A{H}^3=DK.A{B}^2.$

Ta có: $AD.AB=AE.AC\left(cmt\right)$ $\Rightarrow \frac{AD}{AC}=\frac{AE}{AB}$

Xét $\mathrm{\Delta }ADE$ và $\mathrm{\Delta }ACB$ ta có:

$\begin{array}{l}\frac{AD}{AC}=\frac{AE}{AB}\left(cmt\right)\\ \mathrm{\angle }Achung\\ \Rightarrow \mathrm{\angle }\mathrm{\Delta }ADE\sim \mathrm{\Delta }ACB\left(g-c-g\right)\end{array}$

$\Rightarrow \{\begin{array}{l}\mathrm{\angle }ADE=\mathrm{\angle }ACB\\ \mathrm{\angle }AEB=\mathrm{\angle }ABD\end{array}$ (các cặp góc tương ứng)

Ta có: $AM$ là đường trung tuyến ứng với cạnh huyền của $\mathrm{\Delta }ABC$ vuông tại $A$

$\Rightarrow AM=MB=MC\left(=\frac{1}{2}BC\right)$ (tính chất)

$\Rightarrow \mathrm{\Delta }MAC$ cân tại $M$ (định nghĩa)

$\Rightarrow \mathrm{\angle }MAC=\mathrm{\angle }MCA$ hay $\mathrm{\angle }KAE=\mathrm{\angle }ACB$ $\Rightarrow \mathrm{\angle }KAE=\mathrm{\angle }ADE\left(=\mathrm{\angle }ACB\right)$

Xét $\mathrm{\Delta }ADE$ vuông tại $A$ ta có: $\mathrm{\angle }ADE+\mathrm{\angle }AED={90}^0$

$\Rightarrow \mathrm{\angle }KAE+\mathrm{\angle }AED={90}^0$ hay $\mathrm{\angle }KAE+\mathrm{\angle }KEA={90}^0$

$\Rightarrow \mathrm{\Delta }AKE$ vuông tại $K$ hay $AM\mathrm{\perp }DE=\left\{K\right\}\left(dpcm\right).$

+) Chứng minh: $A{H}^3=DK.A{B}^2.$

Xét tứ giác $ADHE$ ta có: $\mathrm{\angle }A=\mathrm{\angle }D=\mathrm{\angle }E={90}^0$

$\Rightarrow ADHE$ là hình chữ nhật (dhnb)

$\Rightarrow AH=DE$ (tính chất hình chữ nhật)

Áp dụng hệ thức lượng trong $\mathrm{\Delta }ADE$ vuông tại $A,$ có đường cao $AK$ ta có:

$A{D}^2=DK.DE=DK.AH\left(AH=DE\right)$

$\Rightarrow DK=\frac{A{D}^2}{AH}.$

$\Rightarrow DK.A{B}^2=\frac{A{D}^2}{AH}.A{B}^2$ $=\frac{{\left(AD.AB\right)}^2}{AH}=\frac{{\left(A{H}^2\right)}^2}{AH}=A{H}^3\left(dpcm\right)$

c) Biết $HB=3cm,HC=7cm.$ Tính $AB,AC,DE$ và $\sqrt[3]{B{D}^2}+\sqrt[3]{C{E}^2}.$

Ta có: $BC=BH+HC=3+7=10cm.$

Áp dụng hệ thức lượng trong $\mathrm{\Delta }ABC$ vuông tại $A,$ có đường cao $AH$ ta có:

$A{H}^2=HB.HC=3.7=21$ $\Rightarrow AH=\sqrt{21}cm$ $\Rightarrow DE=AH=\sqrt{21}cm.$

$A{B}^2=BH.BC=3.10=30$ $\Rightarrow AB=\sqrt{30}cm.$

$A{C}^2=HC.BC=7.10=70$ $\Rightarrow AC=\sqrt{70}cm.$

Áp dụng hệ thức lượng trong $\mathrm{\Delta }ABH$ vuông tại $H,$ có đường cao $HD$ ta có:

$B{H}^2=BD.BA$ $\Rightarrow BD=\frac{B{H}^2}{BA}=\frac{3^2}{\sqrt{30}}=\frac{3\sqrt{30}}{10}cm.$

Áp dụng hệ thức lượng trong $\mathrm{\Delta }AHC$ vuông tại $H,$ có đường cao $HE$ ta có: $C{H}^2=CE.CA$

$$\begin{array}{l}\Rightarrow \sqrt[3]{B{D}^2}+\sqrt[3]{C{E}^2}=\sqrt[3]{{\left(\frac{3\sqrt{30}}{10}\right)}^2}+\sqrt[3]{{\left(\frac{7\sqrt{70}}{10}\right)}^2}\\ =\sqrt[3]{\frac{27}{10}}+\sqrt[3]{\frac{343}{10}}=\frac{3}{\sqrt[3]{10}}+\frac{7}{\sqrt[3]{10}}\\ =\frac{10}{\sqrt[3]{10}}=\sqrt[3]{\frac{{10}^3}{10}}=\sqrt[3]{100}.\end{array}$$

$\Rightarrow CE=\frac{C{H}^2}{CA}=\frac{7^2}{\sqrt{70}}=\frac{7\sqrt{70}}{10}cm.$

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 8

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 8)

Bài 1 (1,5 điểm):

1) Tính giá trị biểu thức $P=\sqrt{125}+\sqrt{20}-\sqrt{180}$.

2) Tìm giá trị $x$ thực biết: $\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4$.

Bài 2 (2 điểm): Rút gọn các biểu thức

1) $A=\frac{1}{2-\sqrt{3}}+\frac{1}{2+\sqrt{3}}$              

2) $B=\sqrt{5+2\sqrt{{\left(1-\sqrt{2}\right)}^2}}$                      

3) $C=\frac{x+\sqrt{x}-2}{\sqrt{x}+2}$ (với $x\ge 0$)

Bài 3 (3 điểm):

Cho các biểu thức: $A=\frac{x-4}{\sqrt{x}-2}$  và  $B=\frac{2}{\sqrt{x}-2}+\frac{3}{\sqrt{x}+2}-\frac{x-5\sqrt{x}+2}{4-x}$ với $x\ge 0;x\ne 4$

1) Tính giá trị của $A$ khi $x=49$.

2) Rút gọn $B$.

3) Với $x>4$, tìm giá trị nhỏ nhất của biểu thức $P=A.B$.

Bài 4 (3 điểm):

Cho $\mathrm{\Delta }ABC$ vuông tại $A,$ đường cao $AH,AB=3cm,BC=6cm.$ Gọi $E,F$ lần lượt là hình chiếu vuông góc của $H$ trên $AB$ và $AC.$

a) Giải $\mathrm{\Delta }ABC.$

b) Tính $AH$ và chứng minh $EF=AH.$

c) Tính $EA.EB+AF.FC.$

Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức $A=\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy$ với $x>0;y>0;x+y\le 1$.

Đáp án và Hướng dẫn làm bài

Bài 1:

Phương pháp:

1)  Rút gọn căn bậc hai bằng công thức: $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}=\{\begin{array}{l}A\sqrt{B}khiA\ge 0\\ -A\sqrt{B}khiA<0\end{array}.$

2) Tìm điều kiện xác định sau đó giải phương trình bằng phương pháp đưa phương trình về dạng phương trình tích sau đó bình phương hai vế. 

Cách giải:

1) Tính giá trị biểu thức $P=\sqrt{125}+\sqrt{20}-\sqrt{180}$.

$\begin{array}{l}P=\sqrt{125}+\sqrt{20}-\sqrt{180}=\sqrt{5^3}+\sqrt{4.5}-\sqrt{36.5}\\ =\sqrt{5^2.5}+\sqrt{2^2.5}-\sqrt{6^2.5}=5\sqrt{5}+2\sqrt{5}-6\sqrt{5}\\ =\sqrt{5}.\end{array}$

Vậy $P=\sqrt{5}$.

2) Tìm giá trị $x$ thực biết: $\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4$.

Điều kiện xác định : $\{\begin{array}{l}x-1\ge 0\\ 9x-9\ge 0\\ 4x-4\ge 0\end{array}\Rightarrow x-1\ge 0\Rightarrow x\ge 1$

$\begin{array}{l}\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4\\ \iff \sqrt{x-1}+\sqrt{9\left(x-1\right)}-\sqrt{4\left(x-1\right)}=4\\ \iff \sqrt{x-1}+3\sqrt{x-1}-2\sqrt{x-1}=4\\ \iff 2\sqrt{x-1}=4\\ \iff \sqrt{x-1}=2\\ \iff x-1=2^2=4\\ \iff x=5\left(tmdk\right)\end{array}$

Vậy phương trình có nghiệm $x=5$.

Bài 2:

Phương pháp:

1) Quy đồng mẫu của các biểu thức để rút gọn

2) Rút gọn căn bậc hai bằng công thức: $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}=\{\begin{array}{l}A\sqrt{B}khiA\ge 0\\ -A\sqrt{B}khiA<0\end{array}.$

3) Phân tích đa thức trên tử số thành nhân tử và rút gọn với mẫu số.

Cách giải:

 $1)A=\frac{1}{2-\sqrt{3}}+\frac{1}{2+\sqrt{3}}=\frac{2+\sqrt{3}+2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\frac{4}{2^2-3}=4$

Vậy $A=4.$

$\begin{array}{l}2)B=\sqrt{5+2\sqrt{{\left(1-\sqrt{2}\right)}^2}}=\sqrt{5+2.\left(\sqrt{2}-1\right)}\\ =\sqrt{5+2\sqrt{2}-2}=\sqrt{3+2\sqrt{2}}\\ =\sqrt{{\left(\sqrt{2}+1\right)}^2}=\sqrt{2}+1.\end{array}$

Vậy $B=\sqrt{2}+1.$

$\begin{array}{l}3)C=\frac{x+\sqrt{x}-2}{\sqrt{x}+2}\left(x\ge 0\right)\\ =\frac{x+2\sqrt{x}-\sqrt{x}-2}{\sqrt{x}+2}=\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+2}=\sqrt{x}-1.\end{array}$

Vậy $C=\sqrt{x}-1$ với $x\ge 0$.

Bài 3:

Phương pháp:

1) Thay giá trị của $x=49$ (tmđk) vào phương trình để tính.

2) Quy đồng, rút gọn phân thức.

3) Phân tích biểu thức P sao cho hợp lí để có thể sử dụng bất đẳng thức Cô-si cho hai số dương.

Cách giải:

1) Tính giá trị của $A$ khi  $x=49$.

Với $x=49$ thỏa mãn điều kiện: $x\ge 0,x\ne 4$

Thay $x=9$  vào biểu thức $A$  ta được:

$A=\frac{49-4}{\sqrt{49}-2}=\frac{45}{7-2}=\frac{45}{5}=9$.

Vậy $A=9$ khi $x=49.$

2) Rút gọn $B$.

Điều kiện: $x\ge 0,x\ne 4.$

$\begin{array}{l}B=\frac{2}{\sqrt{x}-2}+\frac{3}{\sqrt{x}+2}-\frac{x-5\sqrt{x}+2}{4-x}\\ =\frac{2}{\sqrt{x}-2}+\frac{3}{\sqrt{x}+2}+\frac{x-5\sqrt{x}+2}{x-4}\\ =\frac{2}{\sqrt{x}-2}+\frac{3}{\sqrt{x}+2}+\frac{x-5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\frac{2\left(\sqrt{x}+2\right)+3\left(\sqrt{x}-2\right)+x-5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\frac{2\sqrt{x}+4+3\sqrt{x}-6+x-5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\frac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{x}{x-4}.\end{array}$

Vậy $B=\frac{x}{x-4}$ với $x\ge 0;x\ne 4$.

3) Với $x>4$, tìm giá trị nhỏ nhất của biểu thức $P=A.B$.

Với $x>4$, ta có:

$\begin{array}{l}P=A.B=\frac{x-4}{\sqrt{x}-2}.\frac{x}{x-4}=\frac{x}{\sqrt{x}-2}\\ \Rightarrow P=\frac{x-4+4}{\sqrt{x}-2}=\frac{x-4}{\sqrt{x}-2}+\frac{4}{\sqrt{x}-2}\\ =\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}-2}+\frac{4}{\sqrt{x}-2}\\ =\sqrt{x}+2+\frac{4}{\sqrt{x}-2}=\sqrt{x}-2+\frac{4}{\sqrt{x}-2}+4\end{array}$

Khi $x>4$ thì $\Rightarrow \sqrt{x}>2\Rightarrow \{\begin{array}{l}\sqrt{x}-2>0\\ \frac{4}{\sqrt{x}-2}>0\end{array}$

Áp dụng bất đẳng thức Cô-si cho hai số dương $\sqrt{x}-2$ và  $\frac{4}{\sqrt{x}-2}$ ta được:

$\begin{array}{l}\sqrt{x}-2+\frac{4}{\sqrt{x}-2}\ge 2.\sqrt{\left(\sqrt{x}-2\right).\frac{4}{\sqrt{x}-2}}=2\sqrt{4}=4\\ \Rightarrow \sqrt{x}-2+\frac{4}{\sqrt{x}-2}+4\ge 4+4=8hayP\ge 8\end{array}$

Dấu “=” xảy ra $\iff \sqrt{x}-2=\frac{4}{\sqrt{x}-2}\Rightarrow {\left(\sqrt{x}-2\right)}^2=4$

$\iff [\begin{array}{l}\sqrt{x}-2=2\\ \sqrt{x}-2=-2\end{array}\iff [\begin{array}{l}\sqrt{x}=4\\ \sqrt{x}=0\end{array}\iff [\begin{array}{l}x=16\left(tmx>4\right)\\ x=0\left(ktmx>4\right)\end{array}$

Vậy giá trị nhỏ nhất của $P=8$ khi và chỉ khi $x=16$.

Bài 4:

Phương pháp:

a) Sử dụng định lý Pitago và tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài.

b, c) Sử dụng công thức hệ thức lượng trong tam giác vuông để làm bài.

Cách giải:

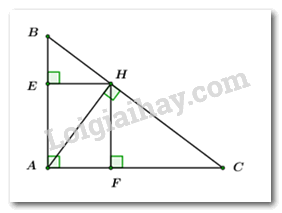
 a) Giải $\mathrm{\Delta }ABC.$

$AC=\sqrt{B{C}^2-A{B}^2}=\sqrt{6^2-3^2}=\sqrt{27}=3\sqrt{3}cm.$Áp dụng định lý Pitago cho $\mathrm{\Delta }ABC$ vuông tại$A$ ta có:

Xét $\mathrm{\Delta }ABC$ vuông tại $A$ ta có:

$\begin{array}{l}\cos \mathrm{\angle }B=\frac{AB}{BC}=\frac{3}{6}=\frac{1}{2}\Rightarrow \mathrm{\angle }B={60}^0\\ \Rightarrow \mathrm{\angle }C={90}^0-\mathrm{\angle }B={90}^0-{60}^0={30}^0.\end{array}$

b) Tính $AH$ và chứng minh $EF=AH.$

Áp dụng hệ thức lượng cho $\mathrm{\Delta }ABC$ vuông tại$A$ có đường cao $AH$ ta có:

$AH=\frac{AB.AC}{BC}=\frac{3.3\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}cm.$

Xét tứ giác $AEHF$ ta có: $\mathrm{\angle }A=\mathrm{\angle }E=\mathrm{\angle }F={90}^0\left(gt\right)$

$\Rightarrow AEHF$ là hình chữ nhật (dhnb).

$\Rightarrow AH=EF$ (hai đường chéo hình chữ nhật).

c) Tính $EA.EB+AF.FC.$

Áp dụng hệ thức lượng cho $\mathrm{\Delta }ABH$ vuông tại $H$ có đường cao $HE$ ta có:

$AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3.3\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}cm.$

Áp dụng hệ thức lượng cho $\mathrm{\Delta }ABH$ vuông tại $H$ có đường cao $HE$ ta có:

$H{E}^2=EA.EB$

Áp dụng hệ thức lượng cho $\mathrm{\Delta }ACH$ vuông tại $H$ có đường cao $HF$ ta có:

$\begin{array}{l}H{F}^2=AF.FC\\ \Rightarrow EB.EA+AF.DC=H{E}^2+H{F}^2=A{H}^2={\left(\frac{3\sqrt{3}}{2}\right)}^2=\frac{27}{4}.\end{array}$

Bài 5:

Tìm giá trị nhỏ nhất của biểu thức $A=\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy$ với $x>0;y>0;x+y\le 1$.

$A=\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\frac{5}{4xy}+\left(\frac{1}{4xy}+4xy\right)$

Áp dụng bất đẳng thức $\frac{a+b}{2}\ge \sqrt{ab}$ với  $a,b>0$

Với  $x>0;y>0;x+y\le 1$, ta có:

 $\frac{1}{x^2+y^2}+\frac{1}{2xy}\ge \frac{2}{\sqrt{\left(x^2+y^2\right).2xy}}\ge 2.\frac{2}{x^2+y^2+2xy}=\frac{4}{{\left(x+y\right)}^2}\ge \frac{4}{1^2}=4\left(dox+y\le 1\right).$

$\begin{array}{l}\frac{5}{4xy}\ge \frac{5}{{\left(x+y\right)}^2}\ge 5\left(dox+y\le 1\right)\\ \frac{1}{4xy}+4xy\ge 2\sqrt{\frac{1}{4xy}.4xy}=2\\ \Rightarrow A\ge 4+5+2=11.\end{array}$

 Dấu “=” xảy ra $\iff \{\begin{array}{l}x=y\\ x+y=1\end{array}\Rightarrow x=y=\frac{1}{2}$

Vậy GTNN của $A$  là $11$  khi và chỉ khi $x=y=\frac{1}{2}$.

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 9

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 9)

Câu 1 (2 điểm): Rút gọn các biểu thức dưới đây:

a. 

b. 

Câu 2 (1 điểm): Tìm điều kiện để các căn thức dưới đây có nghĩa:

a)

b)

Câu 3 (2 điểm): Cho hai biểu thức  và 

a) Rút gọn biểu thức C = A : B

b) Tính giá trị của biểu thức C tại 

Câu 4 (2 điểm): Giải phương trình:

a)

b)

Câu 5 (3 điểm): Cho tam giác ABC, đường cao AH (H ∈ BC) có AB = 6cm, AC = 8cm, BC = 10cm. Trên tia đối của tia BA, lấy điểm D sao cho BD = BC

a) Chứng minh tam giác ABC là tam giác vuông.

b) Tính độ dài của BH, HC và AH.

c). Chứng minh: 

d) Tính diện tích tam giác BCD

Đáp án và Hướng dẫn làm bài

Câu 1

a) 

b. 

Câu 2

a) Để biểu thức  có nghĩa thì 

b) Để biểu thức  có nghĩa thì 

Câu 3

a) ; điều kiện 

; điều kiện 

Vậy 

b) Tại  (tm) thì 

Có 

Vậy tại  thì 

Câu 4

a) 

<=> 

<=> 

<=> 

Vậy S = {-1; 9}

b)  (1)

Điều kiện 

(1) 

Vậy S = {0; 1}

Câu 5

Hình vẽ minh họa:

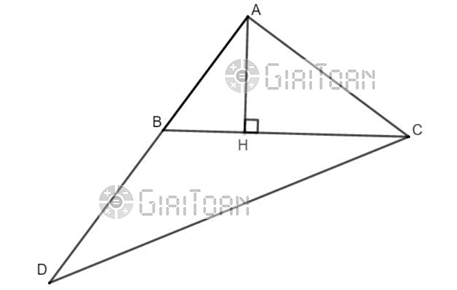
a) Xét ∆ABC có:

=> ABC vuông tại A (Pitago đảo)

b) Xét ∆ABC vuông tại A (cmt), có AH ⊥ BC:

 (hệ thức lượng trong tam giác vuông)

(cm)

 (hệ thức lượng trong tam giác vuông)

(cm)

 (hệ thức lượng trong tam giác vuông)

(cm)

c) + Có AD = AB + BD = 6 + 10 = 16 (cm)

+ Xét ∆ADC vuông tại A có:

(Pitago)

(cm)

+ Có AD.BC = 16.10 = 160

Và 

Vậy 

d)  (cm²)

(cm²)

Vậy S_∆BCD = 64 – 24 = 40 (cm²)

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 10

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 10)

I. Phần trắc nghiệm (2 điểm)

Hãy viết chữ cái in hoa trước phương án đúng trong các câu sau vào bài làm.

Câu 1: Kết quả khai căn của biểu thức  là:

A.	B.
C.	D.

Câu 2: Điều kiện của a để căn thức  có nghĩa:

A.	B.
C.	D.

Câu 3: Kết quả của phép tính  là

A. -2	B. 2
C. -8	D. -5

Câu 4: Giá trị của biểu thức  là:

A.	B.
C. -4	D. 4

Câu 5: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm, kẻ AH vuông góc với BC. Khi đó AH có độ dài là:

A. 6,3	B. 4,8
C. 5,4	D. 5,2

Câu 6: Trong các khẳng định saiu, khẳng định nào sai?

A.	B.
C.	D.

Câu 7: Chọn khẳng định đúng dưới đây

A.	B.
C.	D.

Câu 8: Một cây gỗ cao đặt dựa vào tường biết khoảng cách từ chân cây gỗ đến chân tường là 2m, góc giữa cây gỗ và mặt đất là 60⁰. Hỏi cây gỗ cao bao nhiêu mét?

A. 4m	B. 6m
C. 12m	D. 8m

II. Phần Tự luận

Câu 1 (3 điểm):

Thực hiện các phép tính:

a) 

b) 

c) 

Câu 2 (2 điểm): Cho biểu thức: 

a) Tìm giá trị x để biểu thức A có nghĩa. Rút gọn biểu thức A

b) Tính giá trị của A khi x = 9

c) Tính giá trị của x để biểu thức A = 0,5

Câu 3 (2,5 điểm): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn: BH = 4 cm và HC = 6 cm. Gọi M là trung điểm của AC. Kẻ AK vuông góc với BM (K thuộc BM.

a. Tính độ dài các đoạn AH, AB, AC.

b. Tính số đo góc AMB.

c. Chứng minh: BK.BM = BH.BC.

Câu 4: Tìm tất cả các số dương a, b, c thỏa mãn 

Đáp án và Hướng dẫn làm bài

I. Đáp án phần trắc nghiệm

II. Đáp án phần tự luận

Câu 1

a) Ta có:

b) Ta có:

c) Ta có:

Câu 2

Điều kiện xác định: 

Thay x = 9 vào biểu thức ta có: 

Kết luận khi x = 9 thì 

c. Ta có:

Kết luận A = 2 khi 

Câu 3:

a. Xét tam giác ABC vuông tại A ta có:

Tam giác ABM vuông tại A

b. Tam giác ABM vuông tại A có: 

Tam giác ABM vuông tại A có: 

Câu 4:

Không mất tính tổng quát giả sử

Vậy (1; 2; 2) và các hoán vị của chúng là nghiệm của phương trình.

Đề thi Toán lớp 9 Giữa kì 1 năm 2023 - 2024 có đáp án (20 đề) - Đề 11

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

(Đề 11)

Bài 1: (1,5 điểm) Tính:

Bài 2. (2,0 điểm). Giải các phương trình sau:

Bài 3: (2 điểm) Cho biểu thức 

a) Tính giá trị của A khi a=16

b) Rút gọn biểu thức 

c) So sánh P với 1

Bài 4: (3 điểm)

1. (1 điểm) Một chiếc tivi hình chữ nhật màn hình phẳng 75 inch ( đường chéo tivi dài 75 inch) có góc tạo bời chiều rộng và đường chéo là  Hỏi chiếc tivi ấy có chiều dài, chiều rộng là bao nhiêu cm? Biết 1 inch =2,54 cm. (Kết quả làm tròn đến chữ sổ thập phân thứ nhật)

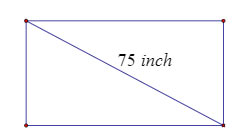
2. Cho tam giác EMF vuông tại M, đường cao MI. Vẽ ,

a) Cho biết  Tính độ dài các đoạn EF, EI, MI.

b) Chứng minh 

Bài 5; Tìm GTNN của biều thức: