Tài liệu Bộ đề thi Toán lớp 9 học kì 1 năm học 2022 - 2023 gồm 15 đề thi tổng hợp từ đề thi môn Toán 9 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi học kì 1 Toán lớp 9. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ 74 Đề thi học kì 1 Toán 9 bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu 

Bộ Đề thi Toán lớp 9 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 1

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

Đề 1:

Bài I (2,0 điểm)

1)    Tính giá trị của biểu thức M =  $\sqrt{{(1-\sqrt{3})}^2}-3\sqrt{12}+\frac{\sqrt{33}}{\sqrt{11}}+1$

2)    Giải phương trình:  $\sqrt{9x-9}-1=\sqrt{x-1}$

Bài II (2,0 điểm)

Cho biểu thức A = $\frac{2\sqrt{x}-1}{\sqrt{x}-3}$ và B = $\frac{2x+3\sqrt{x}+9}{x-9}-\frac{\sqrt{x}}{\sqrt{x}+3}$ với  x ≥ 0; x ≠ 9

1)    Tính giá trị của A khi x = 25

2)    Rút gọn biểu thức B

3)    Cho P =$\frac{\text{A}}{\text{B}}$. Tìm giá trị nhỏ nhất của P.

Bài III (2,0 điểm)

Cho hàm số bậc nhất y = (m – 1)x – 4   (d) (m ≠ 1)

1)    Vẽ đồ thị hàm số khi m = 2

2)    Tìm m để (d) song song với đồ thị hàm số y = - 3x + 2

3)    Tìm m để (d) cắt đồ thị hàm số y = x – 7 (d₂) tại một điểm nằm ở bên trái trục tung.

Bài IV (3,5 điểm)

Cho đường tròn (O;R) đường kính AB. Vẽ tiếp tuyến Bx của (O). Trên cùng một nửa mặt phẳng bờ AB có chứa Bx, lấy điểm M thuộc (O) (M khác A và B) sao cho MA > MB. Tia AM cắt Bx tại C. Từ C kẻ tiếp tuyến thứ hai CD với (O) (D là tiếp điểm).

1)    Chứng minh OC ⊥ BD

2)    Chứng minh bốn điểm O, B, C, D cùng thuộc một đường tròn

3)  Chứng minh  $\left(CMD\right) ̂=\left(CDA\right) ̂$

4)    Kẻ MH vuông góc với AB tại H. Tìm vị trí của M để chu vi tam giác OMH đạt giá trị lớn nhất.

Bài V (0,5 điểm) Cho x, y, z là các số dương thay đổi thỏa mãn: xy + yz + zx = 5

Tìm giá trị nhỏ nhất của biểu thức: T = 3x² + 3y² + z²

........................................................................

Bộ Đề thi Toán lớp 9 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 2

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

Đề 2:

Bài 1 (2,0 điểm)

1.     Thực hiện phép tính:

a)  $2\sqrt{75}-8\sqrt{27}+4\sqrt{48}$    

b) $\frac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{{\left(2-\sqrt{5}\right)}^2}-2\sqrt{5}$  

2.     Giải phương trình:  $x-2\sqrt{x-3}=3$

Bài 2 (2,0 điểm) Cho 2 biểu thức: A = $\frac{\sqrt{x}+1}{\sqrt{x}-2}$ và B =  $\frac{\sqrt{x}+2}{\sqrt{x}-3}+\frac{\sqrt{x}-8}{x-5\sqrt{x}+6}$

(với x ≥ 0; x ≠ 4; x ≠ 9)

a)     Tính giá trị biểu thức A khi x =  $\frac{1}{4}$

b)    Rút gọn biểu thức B

c)     Tìm tất cả các giá trị nguyên của x để B < A

Bài 3 (2,0 điểm)

Cho hàm số y = (m + 1)x + 3 (với m ≠ - 1) có đồ thị là đường thẳng (d)

a)     Vẽ đồ thị hàm số khi m = 2

b)    Tìm m để đường thẳng (d) song song với đường thẳng y = - 2x + 1

c)     Tìm m để đường thẳng (d) cắt hai trục tọa độ Ox, Oy tạo thành một tam giác có diện tích bằng 9.

Bài 4 (3,5 điểm) Cho đường tròn (O;R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB; C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I.

a)     Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn.

b)    Kẻ tiếp tuyến Ax của đường tròn (O;R), tia OI cắt Ax tại M, chứng minh OI.OM = R². Tính độ dài đoạn OI biết OM = 2R và R = 6cm.

c)     Gọi giao điểm của BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.

d)    Giả sử (O;R) cố định, điểm C thay đổi trên đường tròn nhưng vẫn thỏa mãn điều kiện của đề bài. Xác định vị trí của C để chu vi tam giác OHC đạt giá trị lớn nhất? Tìm giá trị lớn nhất đó theo R.

Bài 5 (0,5 điểm) Cho các số thực x, y , z > 0 và x + 2y + 3z ≥ 20

Tìm giá trị nhỏ nhất của biểu thức P =  $x+y+z+\frac{3}{x}+\frac{9}{2y}+\frac{4}{z}$

.....................................................................

Bộ Đề thi Toán lớp 9 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 3

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

Đề 3:

Bài 1 (2,0 điểm) : Cho biểu thức 

1) Tính giá trị của biểu thức A khi x = 16

2) Rút gọn biểu thức 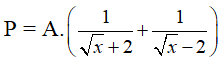. với x > 0; x ≠ 4

3) Tìm các giá trị của x để 

Bài 2 (2,0 điểm) :

1) Thực hiện phép tính: 

2) Giải các phương trình sau:

Bài 3 (2,0 điểm) : Cho hàm số y = (m – 1)x + 3 có đồ thị là đường thẳng (d)

1) Vẽ đường thẳng (d) khi m = 2

2) Tìm m để đường thẳng (d) song song với đường thẳng y = 2x + 1

3) Tính khoảng cách từ gốc tọa độ đến đường thẳng được vẽ ở câu 1

Bài 4 (3,5 điểm) : Cho điểm E thuộc nửa đường tròn tâm O, đường kính MN. Kẻ tiếp tuyến tại N của nửa đường tròn tâm O, tiếp tuyến này cắt đường thẳng ME tại D.

1) Chứng minh rằng: ΔMEN vuông tại E. Từ đó chứng minh DE.DM = DN²

2) Từ O kẻ OI vuông góc với ME (I ∈ ME).

Chứng minh rẳng: 4 điểm O; I; D; N cùng thuộc một đường tròn.

3) Vẽ đường tròn đường kính OD, cắt nửa đường tròn tâm O tại điểm thứ hai là A. Chứng minh rằng: DA là tiếp tuyến của nửa đường tròn tâm O.

4) Chứng minh rằng: 

Bài 5 (0,5 điểm) : Cho x, y là các số dương và 

Tìm giá trị nhỏ nhất của biểu thức P = x + y

.....................................................................

Bộ Đề thi Toán lớp 9 Học kì 1 năm 2022 - 2023 (15 đề) - Đề 4

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2022 - 2023

Môn: Toán 9

Thời gian làm bài: 90 phút

Đề 4:

Bài 1 (2,0 điểm) :

a) Rút gọn biểu thức: 

b) Giải phương trình: 

Bài 2 (2,0 điểm) : Cho hai biểu thức

a) Tính giá trị của biểu thức A khi x = 25

b) Rút gọn biểu thức B

c) Đặt P = A.B. Tìm giá trị nguyên của x để P < 1

Bài 3 (2,0 điểm) : Cho hàm số y = (2 – m)x + m + 1 (với là tham số và m khác 2) có đồ thị là đường thẳng (d).

a) Tìm m để đồ thị hàm số đi qua điểm A(-1;5); vẽ đồ thị hàm số với giá trị của m vừa tìm được

b) Tìm m để đường thẳng (d) cắt đường thẳng y = 3x – 1 tại điểm có hoành độ bằng 2, tìm tọa độ giao điểm.

Bài 4 (3,5 điểm) : Cho đường tròn (O;R) và một điểm A sao cho OA = 2R, vẽ các tiếp tuyến AB, AC với (O;R), B và C là các tiếp điểm. Vẽ đường kính BOD.

a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn

b) Chứng minh rằng: DC // OA

c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh rằng OCEA là hình thang cân.

d) Gọi I là giao điểm của đoạn OA và (O), K là giao điểm của tia SI và AB. Tính theo R diện tích tứ giác AKOS

Bài 5 (0,5 điểm) : Giải phương trình: