Cách tìm tập xác định của hàm số lượng giác

Hoài Phạm Thị Thu Ngày: 08-03-2024 Lớp 11

Tải xuống 8 4 K 25

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Cách tìm tập xác định của hàm số lượng giác Toán lớp 11, tài liệu bao gồm 8 trang, tuyển chọn 12 bài tập trắc nghiệm Cách tìm tập xác định của hàm số lượng giác đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Cách tìm tập xác định của hàm số lượng giác gồm các nội dung sau:

I. Phương pháp giải

- Tóm tắt lý thuyết ngắn gọn cần nhớ

II. Ví dụ minh họa

- Gồm 12 ví dụ minh họa đa dạng cho dạng bài Cách tìm tập xác định của hàm số lượng giác có lời giải chi tiết

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

DẠNG 1. CÁCH TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ LƯỢNG GIÁC

I. PHƯƠNG PHÁP GIẢI

Cách 1

Tìm tập D của x để f(x) có nghĩa, tức là tìm $D = {x \in ℝ | f (x) \in ℝ}$ .

Cách 2

Tìm tập E của x để f(x) không có nghĩa, khi đó tập xác định của hàm số là D = R\E.

CHÚ Ý

A. Với hàm số $f (x)$ cho bởi biểu thức đại số thì ta có:

1. $f (x) = \frac{f_{1} (x)}{f_{2} (x)}$ điều kiện: * $f_{1} (x)$ có nghĩa

* $f_{2} (x)$ có nghĩa và $f_{2} (x) \neq 0$ .

2. $f (x) = \sqrt[2 m]{f_{1} (x)}, (m \in ℕ)$ , điều kiện: $f_{1} (x)$ có nghĩa và $f_{1} (x) \geq 0$ .

3. $f (x) = \frac{f_{1} (x)}{\sqrt[2 m]{f_{2} (x)}}, (m \in)$ , điều kiện: $f_{1} (x), f_{2} (x)$ có nghĩa và $f_{2} (x) > 0$

B. Hàm số $y = s i n x; y = c o s x$ xác định trên $ℝ$ , như vậy

$y = \sin [u (x)]; y = \cos [u (x)]$ xác định khi và chỉ khi $u (x)$ xác định.

* $y = \tan [u (x)]$ có nghĩa khi và chỉ khi $u (x)$ xác định và $u (x) \neq \frac{π}{2} + k π; k \in ℤ$ .

* $y = \cot [u (x)]$ có nghĩa khi và chỉ khi $u (x)$ xác định và $u (x) \neq + k π; k \in ℤ$ .

STUDY TIP

Ở phần này chúng ta chỉ cần nhớ kĩ điều kiện xác định của các hàm số cơ bản như sau:

1. Hàm số y = sinx và y = cosx xác định trên $ℝ$ .

2. Hàm số y = tanx xác định trên $ℝ \ {\frac{π}{2} + k π | k \in ℤ}$

3. Hàm số y = cotx xác định trên $ℝ \ {k π | k \in ℤ}$ .

II. VÍ DỤ MINH HỌA

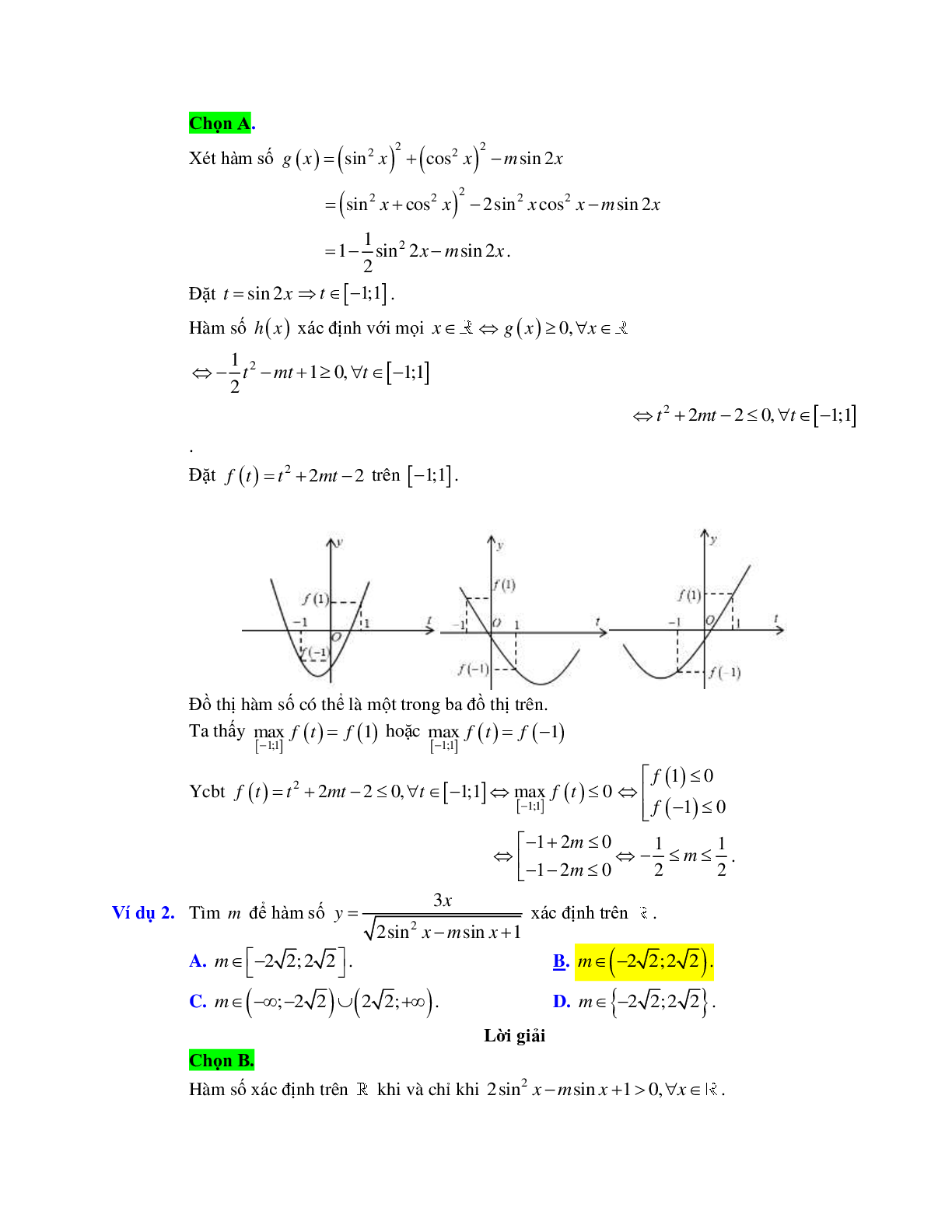
Ví dụ 1. Tập xác định của hàm số $y = \frac{1}{2 \cos x - 1}$ là:

A. $D = ℝ \ {\frac{π}{3} + k 2 π, \frac{5 π}{3} + k 2 π | k \in ℤ}$ B. $D = ℝ \ {\frac{π}{3} + k 2 π | k \in ℤ}$

C. $D = {\frac{π}{3} + k 2 π, \frac{5 π}{3} + k 2 π | k \in ℤ}$ D. $D = ℝ \ {\frac{5 π}{3} + k 2 π | k \in ℤ}$

Xem thêm

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Tài liệu có 8 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Toán 11 tập xác định hàm số lượng giác

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm