Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Hàm số lượng giác Toán lớp 11, tài liệu bao gồm 13 trang, tuyển chọn 6 bài tập Hàm số lượng giác đầy đủ lý thuyết, phương pháp giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Lý thuyết, bài tập về Hàm số lượng giác gồm các nội dung sau:

A. LÝ THUYẾT VỀ HÀM SỐ LƯỢNG GIÁC

1. Hàm số sin và hàm số cosin

a) Hàm số sin

- Định nghĩa:

    Quy tắc đặt tương ứng mỗi số thực x đối với số thực sin x

    sin: R → R

    x → y = sin x

được gọi là hàm số sin, kí hiệu là: y = sinx.

- Tập xác định của hàm số sin là R.

- Là hàm số lẻ.

b) Hàm số côsin

- Định nghĩa:

Quy tắc đặt tương ứng mỗi số thực x đối với số thực cos x

cos: R → R

x → y = cos x

được gọi là hàm số cosin, kí hiệu là: y = cos x.

- Tập xác định của hàm số cosin là R.

- Là hàm số chẵn.

2. Hàm số tang và hàm số cotang

a) Hàm số tang

- Định nghĩa: Hàm số tang là hàm số được xác định bới công thức: 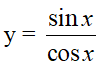 (cos x ≠ 0)

- Kí hiệu là y = tan x

- Tập xác định của hàm số y = tan x là D = R\{π/2 + kπ, k ∈ Z}.

- Là hàm số lẻ.

b) Hàm số cotang

- Định nghĩa:

    Hàm số cotang là hàm số được xác định bới công thức: 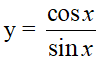 (sin x ≠ 0)

- Kí hiệu là y = cot x

- Tập xác định của hàm số y = cot x là D = R\{kπ, k ∈ Z}.

- Là hàm số lẻ.

3. Tính tuần hoàn của hàm lượng giác

- Các hàm số y = sin x và y = cos x là những hàm số tuần hoàn với chu kì 2π.

- Các hàm số y = tan x và y = cot x là những hàm số tuần hoàn với chu kì π.

4. Sự biến thiên và đồ thị của hàm số lượng giác

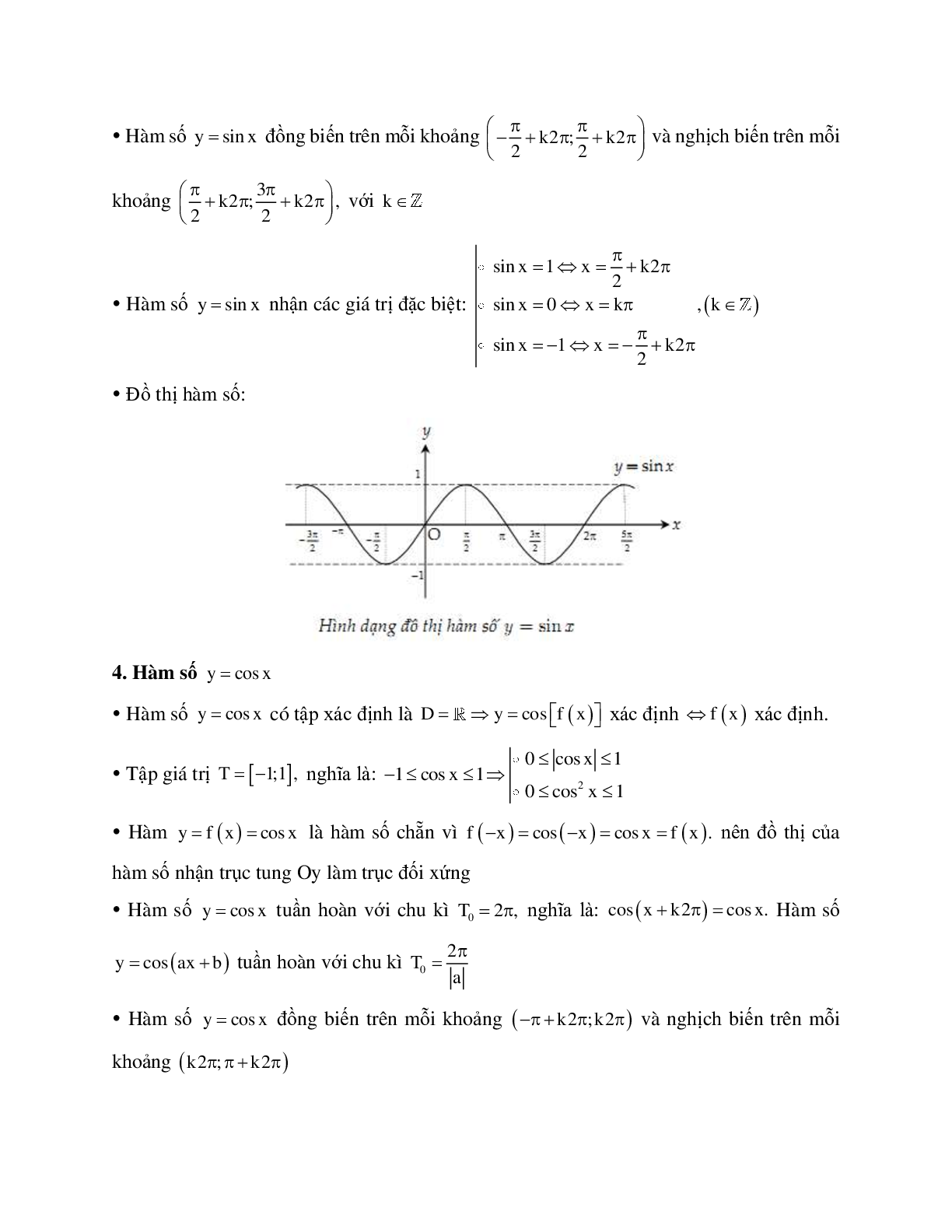
a) Hàm số y = sin x

- Sự biến thiên và đồ thị hàm số y = sin x trên đoạn [0; π]:

    Hàm số y = sin x đồng biến trên [0; π/2] và nghịch biến trên [π/2; π]

- Lưu ý: Vì y = sin x là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn [0; π] qua gốc tọa độ O, ta được đồ thị hàm số trên đoạn [–π; 0]

- Đồ thị hàm số y = sin x trên R: Tịnh tiến liên tiếp đồ thị hàm số trên đoạn [–π; π] theo các vecto v→ = (2π; 0) và –v→ = (–2π; 0)

- Tập giá trị của hàm số y = sin x là [–1; 1]

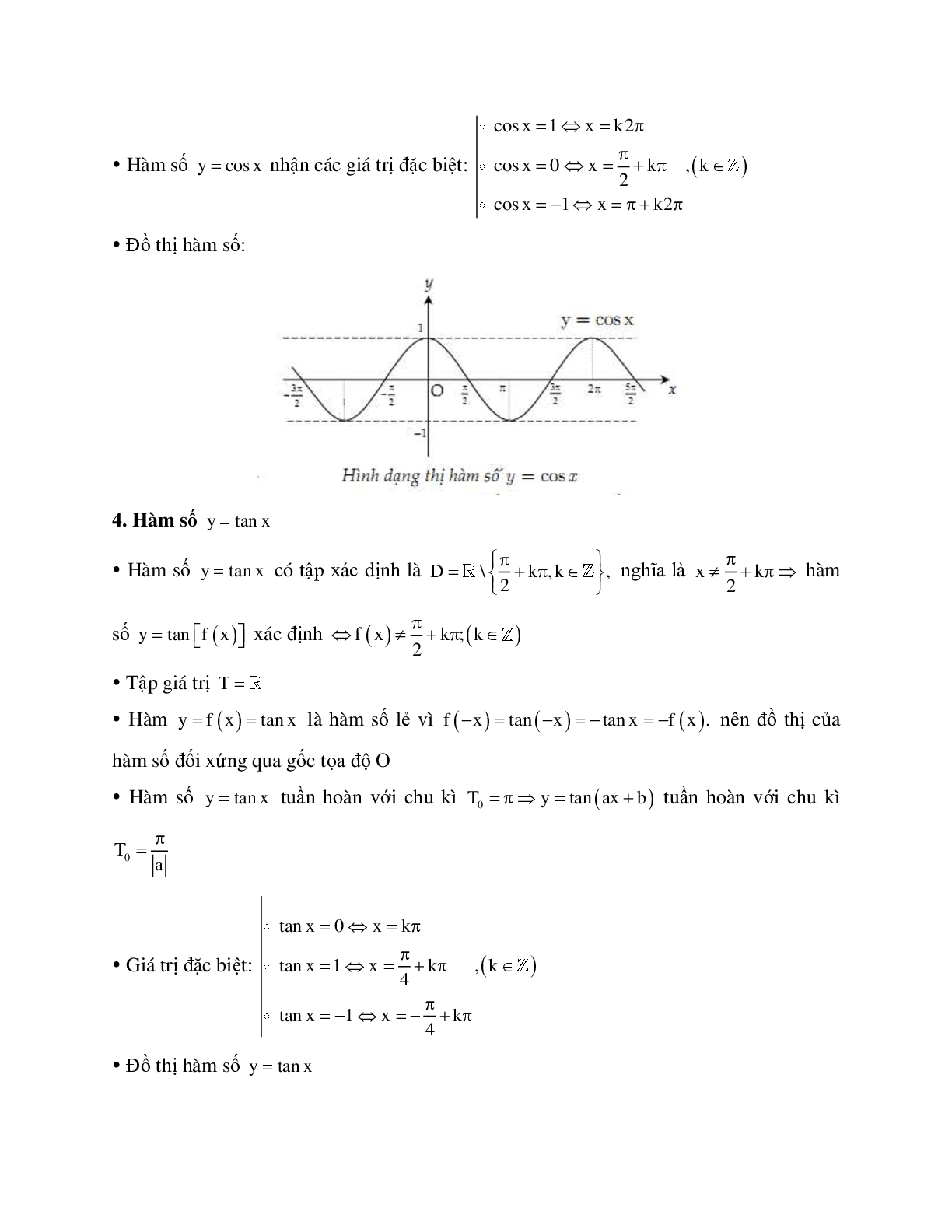
b) Hàm số y = cos x

- Bằng cách tịnh tiến đồ thị hàm số y = sin x theo vectơ u→ = (-π/2; 0), ta được đồ thị của hàm số y = cos x.

- Hàm số y = cos x đồng biến trên [–π; 0] và nghịch biến trên [0; π]

- Tập giá trị của hàm số y = cos x là [–1; 1]

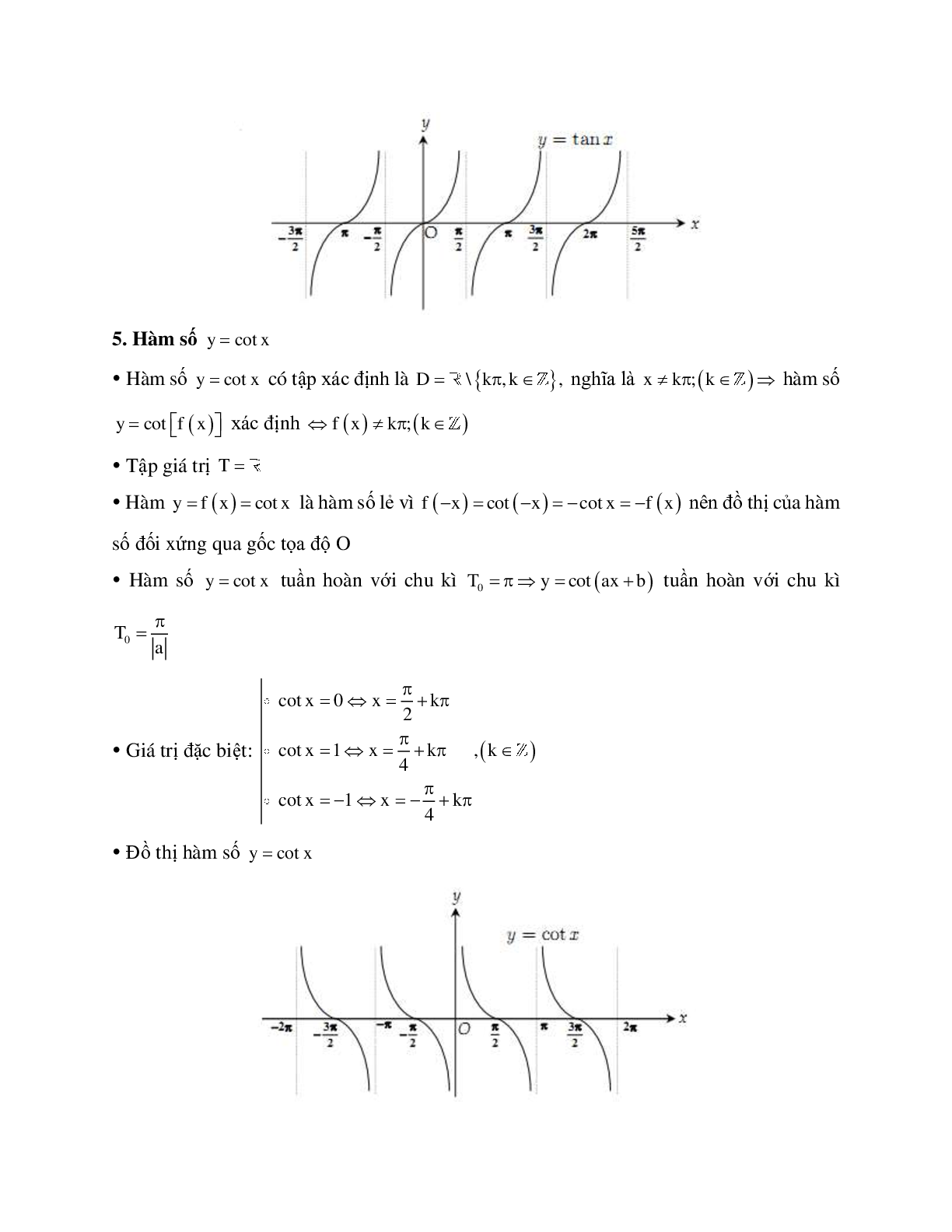
c) Hàm số y = tan x

- Hàm số y = tan x đồng biến trên [0; π/2 )

- Đồ thị hàm số có tâm đối xứng là gốc tọa độ O

=> Lấy đối xứng qua tâm O đồ thị hàm số y = tan x trên [0; π/2 ), ta được đồ thị hàm số y = tan x trên (–π/2; 0]

- Tịnh tiến đồ thị hàm số trên khoảng (–π/2 ; π/2) songsong với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = tan x trên D.

Tập giá trị của hàm số y = tan x là khoảng (–∞; +∞)

d) Hàm số y = cot x

- Hàm số y = cot x nghịch biến trên khoảng (0; π)

- Tịnh tiến đồ thị hàm số trên khoảng (0; π) song song với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = cot x trên D.

- Tập giá trị của hàm số y = cot x là khoảng (–∞; +∞)

B. BÀI TẬP VỀ HÀM SỐ LƯỢNG GIÁC

Bài 1: Hàm số y= 3tan( 2x - π/6) có tập xác định là:

Bài 2: Cho hàm số y = tanx –cotx. Khoảng mà hàm số xác định là:

Bài 3: Hãy chỉ ra hàm số chẵn trong các hàm số sau:

A.y = sinx        B.y= sinx + cotx

C.y= sin(π/2-x)        D.y= sinx.cos²x

Bài 4: Hãy chỉ ra hàm số lẻ trong các hàm số sau:

A.y= cos²x.cos(π/2-x)        B.y= sin²xcosx

C.y= sinx – cosx        D.y= xsinx

Bài 5: Hàm số nào sau đây không có tính chẵn, lẻ?

A.y= cos²xcos(π/2-x)        B.y= sin²x.cosx

C.y= sinx – cosx        D.y= x.sinx

Bài 6: Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. y = cosx + (sinx)²        B. y = sin x + cosx

C. y = -cosx        D. y = sinx.cos3x

Bài 7: Chu kì của hàm số y = cos(x/2) + sinx là:

A.0        B.2π        C.4π        D.6π

Bài 8: Tập xác định D của hàm số sau là

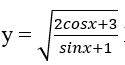
Bài 9: Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y = sinx        B. y = cosx        C. y = tan x        D. y = cotx

Bài 10: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

Bài 11: Tìm tập xác định D của hàm số y = (sinx + 2)/ (sinx.cos²x)

Bài 12: Chu kì của hàm số y = sin5x là:

A.2π        B.5π        C.10π        D.2π/5

Bài 13: Chu kì của hàm số y = sin (x/3) là

A.2π        B.6π        C.π/3        D. 2π/3

Bài 14: Hàm số sau có tập xác định:

Bài 15: Tìm tập giá trị của hàm số sau:

A. D = [0,+∞)        B. D = ∅

C. D = R        D. D = [1,√3]

Bài 16: Hàm số sau có tập xác định là:

Bài 17: Tập xác định của hàm số y = sin√x là:

A.ℝ        B.ℝ\{0}        C.[0;+∞)        D.(0;- ∞)

Bài 18: Hàm số y = 2sinxcosx + cos2x có giá trị lớn nhất là

A.3        B.2√2        C.2        D.√2

Bài 19: Hàm số y = 2cos²x – 1 là hàm tuần hoàn với chu kì:

A.T = π.        B.T = 2π.        C.T = π²        D.T = π/2.

Bài 20: Tìm tập xác định của hàm số sau: y = 2017/sinx

A. D = R        B. D = R\ {kπ, k ∈ Z}

C. D = R\{0}        D. D = R\ {π/2+kπ, k ∈ Z}