Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 11 Bài 1: Hàm lượng giác chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài 1: Hàm lượng giác
Bài 1.1 trang 12 SBT Đại số và giải tích 11: Tìm tập xác định của các hàm số
a)
b)
c)
d)
Phương pháp giải:
a) Phân thức xác định khi
b)
Hàm số xác định khi
c)
Hàm số xác định khi
d)
Phân thức xác định khi
Lời giải:
Điều kiện xác định:
Vậy .
b)
Điều kiện xác định:
Vậy .
c)
Điều kiện xác định:
Vậy .
d)
Điều kiện xác định:
Vậy .
Bài 1.2 trang 12 SBT Đại số và giải tích 11: Tìm tập xác định của các hàm số
a)
b)
c)
d)
Phương pháp giải:
a) Điều kiện xác định của hàm số là
b)
Điều kiện xác định của hàm số là
c)
Điều kiện xác định của hàm số là
d)
Điều kiện xác định của hàm số là
Điều kiện xác định của hàm số là
Lời giải:
Điều kiện xác định:
Ta có:
Vậy .
b)
Điều kiện xác định:
Vậy .
c)
Điều kiện xác định:
(Vì suy ra )
Vậy .
Chú ý:
Các em cũng có thể biến đổi như sau:
d)
Điều kiện xác định:
Vậy tập xác định là:.
Bài 1.3 trang 12 SBT Đại số và giải tích 11: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
a)
b)
c)
d)
Phương pháp giải:
a) Hàm số có
b)
Sử dụng công thức phân tích tổng thành tích thu gọn hàm số.
Sử dụng lý thuyết để đánh giá biểu thức ở trên.
c)
Sử dụng công thức nhân đôi để thu gọn biểu thức
Sử dụng lý thuyết để đánh giá biểu thức ở trên.
d)
Sử dụng công thức nhân đôi để thu gọn biểu thức
Hàm số có
Lời giải:
a)
Vậy GTLN của hàm số là 3 đạt được khi
GTNN của hàm số là 1 đạt được khi
.
b)
Ta có:
Do
Vậy hàm số có GTLN là đạt được khi
GTNN là đạt được khi
c)
Ta có:
Do
Vậy hàm số có GTLN là
đạt được khi
GTNN là đạt được khi
d)
Ta có:
Do
Vậy hàm số có GTLN là đạt được khi
GTNN là đạt được khi
.
Bài 1.4 trang 13 SBT Đại số và giải tích 11: Với những giá trị nào của , ta có mỗi đẳng thức sau ?
a)
b)
c)
d)
Phương pháp giải:
Biến đổi , từ đó suy ra đẳng thức xảy ra khi hai vế xác định.
Tìm ĐKXĐ của các biểu thức xuất hiện trong đẳng thức và kết luận.
Lời giải:
a)
Do đó nếu hai vế xác định.
ĐKXĐ:
Vậy đẳng thức xảy ra khi
b)
Ta có :
Do đó nếu hai vế xác định
ĐKXĐ:
Vậy đẳng thức xảy ra khi .
c)
Ta có :
Do đó nếu hai vế xác định.
ĐKXĐ:
Vậy đẳng thức xảy ra khi .
d)
Ta có:
Do đó nếu hai vế xác định.
xác định khi
xác định khi .
Vậy đẳng thức xảy ra khi .
Bài 1.5 trang 13 SBT Đại số và giải tích 11: Xác định tính chẵn lẻ của các hàm số
a)
b)
c)
d)
Phương pháp giải:
Hàm số với tập xác định gọi là hàm số chẵn nếu
thì và
Hàm số với tập xác định gọi là hàm số lẻ nếu
thì và
Bước 1: tìm TXĐ , chứng minh là tập đối xứng
Bước 2: lấy
Bước 3: xét
Nếu hàm số chẵn
Nếu hàm số lẻ.
Lời giải:
a) Tập xác định: là tập đối xứng
Vậy là hàm số lẻ.
b)
Tập xác định: là tập đối xứng
Vậy là hàm số lẻ.
c)
Do
Tập xác định: là tập đối xứng
Vậy là hàm số chẵn.
d)
Tập xác định: là tập đối xứng
Vậy là hàm số chẵn.
Bài 1.6 trang 13 SBT Đại số và giải tích 11: a) Chứng minh rằng
. Từ đó vẽ đồ thị hàm số
b) Từ đồ thị hàm số , hãy vẽ đồ thị hàm số
Phương pháp giải:
a) Sử dụng công thức
b)
Cách dựng đồ thị hàm số từ đồ thị hàm số :
+ Giữ nguyên phần đồ thị phía trên trục của đồ thị hàm số
+ Lấy đối xứng phần đồ thị phía dưới trục của đồ thị qua
+ Xóa phần đồ thị phía dưới trục của đồ thị hàm số .
Lời giải:
a)
Vậy hàm số là hàm số chẵn, tuần hoàn, có chu kỳ .
Đồ thị hàm số đi qua các điểm
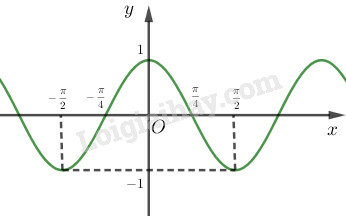
b)
Đồ thị hàm số gồm:
+ Phần đồ thị phía trên trục của đồ thị hàm số
+ Phần đồ thị có được từ việc lấy đối xứng phần đồ thị phía dưới trục của đồ thị hàm số .
Đồ thị hàm số là:
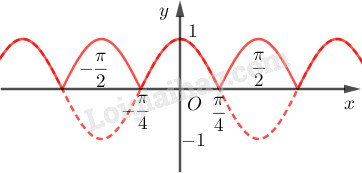
Bài 1.7 trang 13 SBT Đại số và giải tích 11: Tập xác định của hàm số
là
A.
B.
C.
D.
Phương pháp giải:
Điều kiện xác định của hàm số là .
Lời giải:
ĐKXĐ:
Đáp án: A
Bài 1.8 trang 13 SBT Đại số và giải tích 11: Tập xác định của hàm số
là
A.
B.
C.
D.
Phương pháp giải:
Điều kiện xác định của hàm số là
Lời giải:
ĐKXĐ:
Vậy
Đáp án :B
Cách khác:
Hàm số không xác định khi cotx = 0 hoặc khi cotx không xác định
Tức là khi x = kπ hoặc x = π/2 + kπ, k ∈ Z.
Gộp hai giá trị này lại ta được kết quả x = kπ/2, k ∈ Z.
Vậy tập xác định là R \ {π/2+kπ,k ∈ Z }
Bài 1.9 trang 13 SBT Đại số và giải tích 11: Tập xác định của hàm số là
A.
B.
C.
D.
Phương pháp giải:
Hàm số xác định khi .
Hàm số xác định khi .
Lời giải:
ĐKXĐ:
Vậy hay
Đáp án: C.
Cách khác:
Hàm số không xác định khi tanx không xác định hoặc sinx = 1
Tức là khi x = π/2+kπ, hoặc x = π/2+k2π, k ∈ Z.
Gộp hai giá trị này lại ta được kết quả x = π/2+kπ, k ∈ Z.
Vậy tập xác định là R \ {π/2+kπ,k ∈ Z}.
Bài 1.10 trang 14 SBT Đại số và giải tích 11: Tập xác định của hàm số
là
A.
B.
C.
D.
Phương pháp giải:
Hàm số xác định khi .
Hàm số xác định khi .
Lời giải:
Hàm số không xác định khi
Vậy tập xác định là
Đáp án: D.
Cách trắc nghiệm.
Xét các phương án
Với x = π/3 thì tan x = √3 nên hàm số không xác định, do đó các phương án A và B bị loại.
Với x=0 thì nên hàm số không xác định, mà x=0 lại thuộc tập hợp đáp án C nên loại C.
Bài 1.11 trang 14 SBT Đại số và giải tích 11: Tìm giá trị nhỏ nhất của hàm số
là
A. B.
C. D.
Phương pháp giải:
Sử dụng công thức tổng thành tích để rút gọn hàm số.
Hàm số có
Lời giải:
Ta có:
Mà
Vậy giá trị nhỏ nhất của hàm số là đạt được khi .
Đáp án C.
Chú ý:
Hàm số đạt giá trị nhỏ nhất khi cosx + sinx đạt giá trị lớn nhất.
Mà (cosx + sinx)2 = 1 + sin2x ≤ 2.
Giá trị lớn nhất của (cosx + sinx)2 bằng 2, đạt được khi sin2x = 1.
Vậy cosx + sinx đạt giá trị lớn nhất bằng √2.
Từ đó suy ra GTNN của hàm số đã cho.
Bài 1.12 trang 14 SBT Đại số và giải tích 11: Tìm giá trị lớn nhất của hàm số
là
A. B.
C. D.
Phương pháp giải:
Hàm số đạt giá trị lớn nhất khi đạt giá trị lớn nhất.
Sử dụng .
Lời giải:
Vậy giá trị lớn nhất của hàm số là đạt được khi .
Đáp án B.
Cách trắc nghiệm:
Với x = 0 ta thấy y = 3 đều lớn hơn các giá trị trong các phương án A, C, D nên các phương án này bị loại.
Bài 1.13 trang 14 SBT Đại số và giải tích 11: Giá trị nhỏ nhất và lớn nhất của hàm số tương ứng là
A. và B. và
C. và D. và
Phương pháp giải:
Biến đổi về dạng biểu thức chỉ chứa hoặc .
Ta có và từ đó suy ra được giá trị lớn nhất và nhỏ nhất của hàm số.
Lời giải:
Mà
Vậy giá trị nhỏ nhất của hàm số là đạt được khi ,
Giá trị lớn nhất của hàm số là đạt được khi .
Đáp án A.
Cách trắc nghiệm:
Khi x = 0 thì y = 1 lớn hơn 3/4, lớn hơn √2/2 và lớn hơn √3/2, nên ba phương án B, C, D bị loại.

