Với giải Bài 3 trang 100 Toán 11 Tập 1 Cánh diều chi tiết trong Bài 2: Hai đường thẳng song song trong không gian giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 2: Hai đường thẳng song song trong không gian
Bài 3 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, AB, SD. Xác định giao tuyến của mỗi cặp mặt phẳng sau: (SAD) và (SBC); (MNP) và (ABCD).
Lời giải:
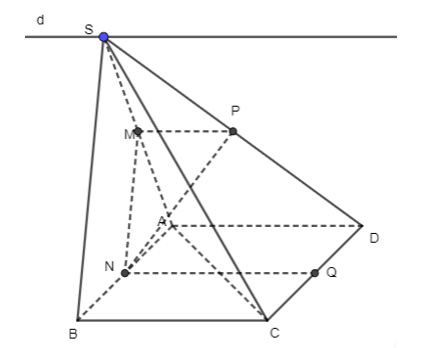
+) Ta có: ABCD là hình bình hành nên AD // BC
Mà AB ⊂ (SAB);
BC ⊂ (SBC);
S ∈ (SAB) và S ∈ (SBC).
Vì vậy giao tuyến của hai mặt phẳng là đường thẳng d đi qua S và song song với AD và BC.
Vậy (SAB) ∩ (SBC) = d.
+) Trong tam giác SAD, có: M, P lần lượt là trung điểm của SA, SD
Do đó MP là đường trung bình nên MP // AD.
Mà MP ⊂ (MNP);
AD ⊂ (ABCD);
N ∈ (MNP) và N ∈ (ABCD).
Vì vậy giao tuyến của hai mặt phẳng là đường thẳng đi qua N và song song với AD và BC, cắt CD tại Q.
Vậy (MNP) ∩ (ABCD) = NQ.
Sơ đồ tư duy hai đường thẳng song song.

Xem thêm các lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Câu hỏi khởi động trang 95 Toán 11 Tập 1: Trong thực tế, ta quan sát thấy nhiều hình ảnh gợi nên những đường thẳng song song với nhau. Chẳng hạn các cột treo cờ của tổ chức các nước thành viên ASEAN (Hình 30)....
Hoạt động 1 trang 95 Toán 11 Tập 1: a) Hãy nêu các vị trí tương đối của hai đường thẳng trong mặt phẳng....
Luyện tập 1 trang 97 Toán 11 Tập 1: Quan sát một phần căn phòng (Hình 35), hãy cho biết vị trí tương đối của các cặp đường thẳng a và b; a và c; b và c....
Hoạt động 2 trang 97 Toán 11 Tập 1: Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d....
Hoạt động 3 trang 97 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a = (P) ∩ (R), b = (Q) ∩ (R), c = (P) ∩ (Q).....
Luyện tập 2 trang 99 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAD) và (SBC).....
Hoạt động 4 trang 99 Toán 11 Tập 1: Trong mặt phẳng, hãy nêu vị trí tương đối của hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba......
Luyện tập 3 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các đoạn thẳng SA, SC. Lấy các điểm P, Q lần lượt thuộc các đoạn thẳng AB, BC sao cho . Chứng minh rằng MN song song với PQ.....
Bài 1 trang 100 Toán 11 Tập 1: Quan sát phòng học của lớp và nêu lên hình ảnh của hai đường thẳng song song, cắt nhau và chéo nhau.....
Bài 2 trang 100 Toán 11 Tập 1: Quan sát Hình 43 và cho biết vị trí tương đối của hai trong ba cột tuabin gió có trong hình.....
Bài 3 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, AB, SD. Xác định giao tuyến của mỗi cặp mặt phẳng sau: (SAD) và (SBC); (MNP) và (ABCD)......
Bài 4 trang 100 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G1, G2 lần lượt là trọng tâm của các tam giác ABC, ABD. Chứng minh rằng đường thẳng G1G2 song song với đường thẳng CD.....
Bài 5 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD......
Bài 6 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.....
Bài 7 trang 100 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh BC, CD. Trên cạnh AC lấy điểm K. Gọi M là giao điểm của BK và AI, N là giao điểm của DK và AJ. Chứng minh rằng đường thẳng MN song song với đường thẳng BD.....
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
