Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 5: Hình lăng trụ và hình hộp chi tiết sách Toán 11 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 5: Hình lăng trụ và hình hộp

Giải Toán 11 trang 110 Tập 1

Câu hỏi khởi động trang 110 Toán 11 Tập 1: Trong thực tiễn, ta thường gặp nhiều đồ dùng, vật thể gợi nên hình ảnh hình lăng trụ, hình hộp. Chẳng hạn: Khung lịch để bàn (Hình 68); Tháp đôi Puerta de Europa ở Madrid, Tây Ban Nha (Hình 69), …

Hình lăng trụ và hình hộp là hình như thế nào?

Lời giải:

Sau bài học này, chúng ta giải quyết được câu hỏi trên như sau:

Hình gồm hai đa giác A₁A₂…A_n, A₁’A₂’…A_n’ và các bình bình hành A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, …, A_nA₁A₁’A_n’ được gọi là hình lăng trụ, kí hiệu là A₁A₂…A_n.A₁’A₂’…A_n’.

Hình hộp là hình lăng trụ có đáy là hình bình hành.

I. Hình lăng trụ

Hoạt động 1 trang 110 Toán 11 Tập 1: Cho hai mặt phẳng song song (P) và (P’). Trong mặt phẳng (P), cho đa giác A₁A₂….A_n. Qua các đỉnh A₁, A₂, ..., A_n vẽ các đường thẳng song song với nhau và cắt mặt phẳng (P’) lần lượt tại A₁’, A₂­’, ..., A_n’ (Hình 70 minh hoạ cho trường hợp n = 5).

a) Các tứ giác A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, …, A_nA₁A₁’A_n’ là những hình gì?

b) Các cạnh tương ứng của hai đa giác A₁A₂…A_n và A₁’A₂’…A_n’ có đặc điểm gì?

Lời giải:

a) Ta có: (P) // (P’);

               (A₁A₂A₂’A₁’) ∩ (P) = A₁A₂;

               (A₁A₂A₂’A₁’) ∩ (P’) = A₁’A₂’.

Do đó A₁A₂ // A₁’A₂’.

Trong mp (A₁A₂A₂’A₁’), tứ giác A₁A₂A₂’A₁’ có A₁A₁’ // A₂A₂’ và A₁A₂ // A₁’A₂’

Do đó A₁A₂A₂’A₁’ là hình bình hành.

Chứng minh tương tự ta có: các tứ giác A₂A₃A₃’A₂’, …, A_nA₁A₁’A_n’ cũng là những hình bình hành.

Vậy các tứ giác A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, …, A_nA₁A₁’A_n’ là những hình bình hành.

b) Theo câu a, A₁A₂A₂’A₁’ là hình bình hành nên A₁A₂ = A₁’A₂’

Tương tự như vậy, ta kết luận các cạnh tương ứng của hai đa giác A₁A₂…A_n và A₁’A₂’…A_n’ có độ dài bằng nhau.

Giải Toán 11 trang 111 Tập 1

Hoạt động 2 trang 111 Toán 11 Tập 1: Từ định nghĩa hình lăng trụ, nhận xét đặc điểm các mặt bên, cạnh bên và hai mặt đáy của hình lăng trụ.

Lời giải:

Từ định nghĩa hình lăng trụ, ta có các nhận xét sau:

• Các cạnh bên của hình lăng trụ song song và bằng nhau.

• Các mặt bên của hình lăng trụ là các hình bình hành.

• Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Luyện tập 1 trang 111 Toán 11 Tập 1: Cho một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ.

Lời giải:

Gợi ý một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ:

II. Hình hộp

Hoạt động 3 trang 111 Toán 11 Tập 1: Vẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành.

Lời giải:

Hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành:

Giải Toán 11 trang 112 Tập 1

Luyện tập 2 trang 112 Toán 11 Tập 1: Hãy liệt kê các đường chéo của hình hộp ABCD.A’B’C’D’ (Hình 73).

Lời giải:

Nối AC’, BD’, CA’, DB’.

Các đường chéo của hình hộp ABCD.A’B’C’D’ là các đoạn thẳng AC’, BD’, CA’, DB’.

Hoạt động 4 trang 112 Toán 11 Tập 1: Nêu nhận xét gì về hai mặt phẳng chứa hai mặt đối diện của hình hộp.

Lời giải:

Nhận xét: Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.

Giải Toán 11 trang 113 Tập 1

Luyện tập 3 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua một điểm.

Lời giải:

Trong mặt phẳng (ABC’D’), xét tứ giác ABC’D’ có:

     AB // C’D’ (cùng song song với DC);

     AB = C’D’ (cùng bằng DC)

Do đó tứ giác ABC’D’ là hình bình hành.

Suy ra hai đường chéo AC’ và BD’ cắt nhau tại trung điểm O của mỗi đường.

Khi đó (ABC’D’) đi qua điểm O.

Tương tự ta cũng có tứ giác BCD’A’ là hình bình hành có hai đường chéo BD’ và CA’ cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD’, do đó O là trung điểm của CA’ và (BCD’A’) đi qua O.

Chứng minh tương tự với các mp(CDA’B’), (DAB’C’) thì các mặt phẳng này cũng đi qua điểm O.

Vậy bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua điểm, điểm O là giao điểm các đường chéo của hình hộp.

Bài tập

Bài 1 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C D’.

a) Chứng minh rằng (ACB’) // (A’C’D).

b) Gọi G₁, G₂ lần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D). Chứng minh rằng G₁, G₂ lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.

c) Chứng minh rằng BG₁ = G₁G₂ = D’G₂.

Lời giải:

a)

Ta có: (ABCD) // (A’B’C’D’) ( do ABCD.A’B’C’D’ là hình hộp);

           (ABCD) ∩ (ACC’A’) = AC;

           (A’B’C’D’) ∩ (ACC’A’) = A’C’.

Do đó AC // A’C’.

Mà A’C’ ⊂ (A’C’D) nên AC // (A’C’D).

Chứng minh tương tự ta cũng có AB’ // DC’ mà DC’ ⊂ (A’C’D) nên AB’ // (A’C’D).

Ta có: AC // (A’C’D);

          AB’ // (A’C’D);

          AC, AB’ cắt nhau tại điểm A và cùng nằm trong mp(ACB’).

Do đó (ACB’) // (A’C’D).

b)

• Gọi O là tâm hình bình hành đáy ABCD, I là giao điểm của BD’ và DB’.

Tứ giác BDD’B’ có BB’ // DD’ và BB’ = DD’ nên là hình bình hành.

Do đó hai đường chéo BD’ và DB’ cắt nhau tại trung điểm I của mỗi đường.

Trong mp(BDD’B’), BD’ cắt B’O tại G₁.

Mà B’O ⊂ (ACB’) nên G₁ là giao điểm của BD’ với (ACB’).

Trong mp(BDD’B’), xét $∆$BDB’ có hai đường trung tuyến BI, B’O cắt nhau tại G₁ nên G₁ là trọng tâm của DBDB’

Do đó $\frac{B^{\text{'}}{G}_1}{BO}=\frac{2}{3}$

Trong (ACB’), xét $∆$ACB’ có B’O là đường trung tuyến và $\frac{B^{\text{'}}{G}_1}{BO}=\frac{2}{3}$

Suy ra G₁ là trọng tâm của $∆$ACB’.

• Gọi O’ là tâm hình bình hành đáy A’B’C’D’.

Chứng minh tương tự như trên ta cũng có: G₂ là trọng tâm của $∆$DD’B’ nên $\frac{D{G}_2}{D{O}^{\text{'}}}=\frac{2}{3}$

Trong (A’C’D), $∆$A’C’D có DO’ là đường trung tuyến và  $\frac{D{G}_2}{D{O}^{\text{'}}}=\frac{2}{3}$

Suy ra G₂ là trọng tâm của $∆$A’C’D.

c) Theo chứng minh câu b, ta có:

• G₁ là trọng tâm của $∆$BDB’ nên $\frac{B{G}_1}{BI}=\frac{2}{3}$  và $\frac{I{G}_1}{B{G}_1}=\frac{1}{2}$

• G₂ là trọng tâm của  $∆$DD’B’ nên $\frac{D^{\text{'}}{G}_2}{D^{\text{'}}I}=\frac{2}{3}$  và $\frac{I{G}_2}{D^{\text{'}}{G}_2}=\frac{1}{2}$

Do đó $\frac{B{G}_1}{BI}=\frac{D^{\text{'}}{G}_2}{D^{\text{'}}I}=\frac{2}{3}$  và $\frac{I{G}_1}{B{G}_1}=\frac{I{G}_2}{D^{\text{'}}{G}_2}=\frac{1}{2}$

Ta có: $\frac{B{G}_1}{BI}=\frac{D^{\text{'}}{G}_2}{D^{\text{'}}I}$ và BI = D’I (do I là trung điểm của BD’)

Suy ra BG₁ = D’G₂.

Lại có $\frac{I{G}_1}{B{G}_1}=\frac{I{G}_2}{D^{\text{'}}{G}_2}=\frac{1}{2}$  nên IG₁ = IG₂ = $\frac{1}{2}$ BG₁

Do đó G₁G₂ = IG₁ + IG₂ = $\frac{1}{2}$ BG₁ + $\frac{1}{2}$ BG₁ = BG₁.

Vậy BG₁ = G₁G₂ = D’G₂.

Bài 2 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA’, C’D’, AD’. Chứng minh rằng:

a) NQ // A’D’ và NQ = $\frac{1}{2}$ A’D’;

b) Tứ giác MNQC là hình bình hành;

c) MN // (ACD’);

d) (MNP) // (ACD’).

Lời giải:

a)

Trong mp(ADD’A’), xét DAA’D’ có N, Q lần lượt là trung điểm của AA’ và AD’

Do đó NQ là đường trung bình của tam giác

Suy ra NQ // A’D’ và NQ = $\frac{1}{2}$ A’D’.

b)

Ta có: A’D’ // AD // BC, mà NQ // A’D’ (câu a) nên NQ // BC hay NQ // MC.

Ta cũng có A’D’ = AD = BC, mà NQ = $\frac{1}{2}$ A’D’ (câu a) nên NQ = $\frac{1}{2}$ BC

Lại có BM = MC = $\frac{1}{2}$ BC (do M là trung điểm BC)

Do đó NQ = MC.

Tứ giác MNQC có NQ // MC và NQ = MC nên là MNQC hình bình hành.

c)

Do MNQC hình bình hành nên MN // QC

Mà QC ⊂ (ACD’) nên MN // (ACD’).

d)

Gọi O là trung điểm của ABCD.

Trong (ABCD), xét DABC có O, M lần lượt là trung điểm của AC, BC nên OM là đường trung bình của tam giác

Do đó OM // AB và OM = $\frac{1}{2}$ AB.

Mà AB // D’P nên OM // D’P.

Lại có D’P = $\frac{1}{2}$ D’C’ và D’C’ = AB nên OM = D’P.

Xét tứ giác D’PMO có OM // D’P và OM = D’P nên là hình bình hành

Suy ra PM // D’O

Mà D’O ⊂ (ACD’) nên PM // (ACD’).

Ta có: MN // (ACD’);

           PM // (ACD’);

           MN, PM cắt nhau tại điểm M và cùng nằm trong mp(MNP)

Do đó (MNP) // (ACD’).

Bài 3 trang 113 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B’.

a) Chứng minh rằng EF // (BCC’B’).

b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF.

Lời giải:

a)

Gọi M là trung điểm của BC.

Trong mp(ABC), xét $∆$ABC có E, M lần lượt là trung điểm của AC, BC nên EM là đường trung bình của tam giác

Do đó EM // AB và EM = $\frac{1}{2}$ AB.

Mà AB // A’B’ nên EM // A’B’ hay EM // FB’.

Lại có AB = A’B’ và FB’ = $\frac{1}{2}$ A’B’ nên EM = FB’.

Trong mp(EMB’F), xét tứ giác EMB’F có EM // FB’ và EM = FB’ nên là hình bình hành.

Do đó EF // B’M, mà B’M ⊂ (BCC’B’) nên EF // (BCC’B’).

b)

Gọi N là trung điểm của AB.

Trong mp(ABB’A’), xét hình bình hành ABB’A’ cũng là hình thang có N, F lần lượt là trung điểm của AB, A’B’ nên NF là đường trung bình của hình thang

Do đó NF // BB’ và $NF=\frac{A{A}^{\text{'}}+B{B}^{\text{'}}}{2}=\frac{2B{B}^{\text{'}}}{2}=B{B}^{\text{'}}$ .

Mà BB’ // CC’ nên NF // CC’.

Lại có BB’ = CC’ nên NF = CC’.

Trong mp(NFC’C), xét tứ giác NFC’C có NF // CC’ và NF = CC’ nên là hình bình hành.

Do đó hai đường chéo CF và NC’ cắt nhau tại trung điểm của mỗi đường.

Lại có NC’ ⊂ (ABC’) nên CF cắt (ABC’) tại trung điểm I của CF.

Vậy CF cắt (ABC’) tại trung điểm I của CF.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Hình lăng trụ và hình hộp

Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian

Bài tập cuối chương 4

Lý thuyết Hình lăng trụ và hình hộp

I. Hình lăng trụ

1. Định nghĩa

- Hình gồm hai đa giác $A_1{A}_2...A_n$, ${A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$ và các tứ giác $A_1{A_1}^{\prime }{A_2}^{\prime }{A}_2$,$A_2{A_2}^{\prime }{A_3}^{\prime }{A}_3$,…,$A_n{A_n}^{\prime }{A_1}^{\prime }{A}_1$ được gọi là hình lăng trụ và kí hiệu là $A_1{A}_2...A_n.{A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$.

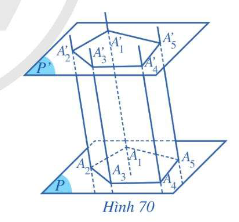
- Trong hình lăng trụ $A_1{A}_2...A_n.{A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$

+ Các điểm $A_1,A_2,...,A_n$ và ${A_1}^{\prime },{A_2}^{\prime },...,{A_n}^{\prime }$ được gọi là các đỉnh.

+ Các đoạn thẳng $A_1{A_1}^{\prime },A_2{A_2}^{\prime },...,A_n{A_n}^{\prime }$ được gọi là các cạnh bên, các đoạn thẳng.$A_1{A}_2,A_2{A}_3,...,A_n{A}_1$và ${A_1}^{\prime }{A_2}^{\prime },{A_2}^{\prime }{A_3}^{\prime },...,{A_n}^{\prime }{A_1}^{\prime }$ gọi là cạnh  đáy của hình trụ.

+ Hai đa giác $A_1{A}_2...A_n$và ${A_1}^{\prime }{A_2}^{\prime }...{A_n}^{\prime }$ được gọi là hai mặt đáy của hình lăng trụ.

+ Các tứ giác $A_1{A_1}^{\prime }{A_2}^{\prime }{A}_2$,$A_2{A_2}^{\prime }{A_3}^{\prime }{A}_3$,…,$A_n{A_n}^{\prime }{A_1}^{\prime }{A}_1$ gọi là các mặt bên của hình trụ.

* Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,… thì lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác.

2. Tính chất

- Các cạnh bên của hình lăng trụ song song và bằng nhau.

- Các mặt bên của hình lăng trụ là các hình bình hành.

- Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.

II. Hình hộp

1. Định nghĩa

- Hình hộp là hình lăng trụ có đáy là hình bình hành.

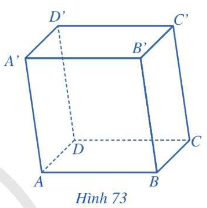
- Trong mỗi hình hộp, ta gọi:

+ Hai mặt không có đỉnh chung là hai mặt đối diện.

+ Hai cạnh song song không nằm trong một mặt phẳng là hai cạnh đối diện.

+ Hai đỉnh không thuộc cùng một mặt là hai đỉnh đối diện.

+ Đoạn thẳng nối hai đỉnh đối diện là đường chéo.

2. Tính chất

- Các mặt của hình hộp là hình bình hành.

- Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.