Với giải HĐ 3 trang 121 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 17:Hàm số liên tục giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 17: Hàm số liên tục
HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x2 và g(x) = – x + 1.
a) Xét tính liên tục của hai hàm số trên tại x = 1.
b) Tính 
và so sánh L với f(1) + g(1).
Lời giải:
a) Hàm số f(x) = x2 và g(x) = – x + 1 là các hàm đa thức nên nó liên tục trên ℝ.
Do đó, hai hàm số f(x) và g(x) đều liên tục tại x = 1.
b) Ta có: f(x) + g(x) = x2 + (– x + 1) = x2 – x + 1.
Do đó, 
.
Lại có, f(1) = 12 = 1; g(1) = – 1 + 1 = 0, do đó f(1) + g(1) = 1 + 0 = 1.
Vậy L = f(1) + g(1) = 1.
Lý thuyết Một số tính chất cơ bản
Giả sử hai hàm số và liên tục tại điểm . Khi đó:
a, Các hàm số và liên tục tại điểm .
b, Hàm số liên tục tại điểm nếu .
Video bài giảng Toán 11 Bài 17: Hàm số liên tục - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 119 Toán 11 Tập 1: Nhận biết tính liên tục của hàm số tại một điểm.....
Luyện tập 1 trang 120 Toán 11 Tập 1: Xét tính liên tục của hàm số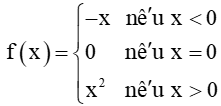 
tại điểm x0 = 0.....
HĐ2 trang 120 Toán 11 Tập 1: Cho hai hàm số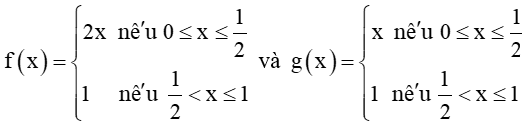 
với đồ thị tương ứng như Hình 5.7.....
Luyện tập 2 trang 121 Toán 11 Tập 1: Tìm các khoảng trên đó hàm số liên tục.....
HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x2 và g(x) = – x + 1......
Bài 5.16 trang 122 Toán 11 Tập 1 :Tìm giá trị của tham số m để hàm sốliên tục trên ℝ....
Bài 5.17 trang 122 Toán 11 Tập 1: Một bảng giá cước taxi được cho như sau:.....
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
. Tính g(1)....
