Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Hàm số liên tục, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hàm số liên tục. Mời các bạn đón xem:

Bài tập Toán 11 Hàm số liên tục

A. Bài tập Hàm số liên tục

Bài 1: Cho hàm số f(x) = 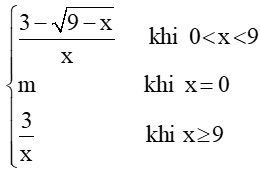. Tìm giá trị của m để f(x) liên tục trên [0; +∞).

Hướng dẫn giải

+) Với x ∈ (0; 9): f(x) = $\frac{3-\sqrt{9-x}}{x}$ liên tục trên (0; 9).

+) Với x ∈ [9; +∞) thì f(x) = $\frac{3}{x}$ liên tục trên [9; +∞).

+) Tại x = 0 ta có f(0) = m

Vậy để hàm số liên tục trên [0; +∞) khi nó phải liên tục tại x = 0.

Suy ra: $\underset{x\to 0^{+}}{\lim }$f(x) = m$\Rightarrow$m = $\frac{1}{6}$.

Vậy m = $\frac{1}{6}$ thì f(x) liên tục trên [0; +∞).

Bài 2: Cho hàm số f(x) = 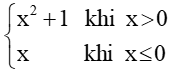. Xét tính liên tục của hàm số tại x = 0.

Hướng dẫn giải

Ta có: f(0) = 0

$\underset{x\to 0^{+}}{\lim }$f(x) = $\underset{x\to 0^{+}}{\lim }$(x²+1) = 1

$\underset{x\to 0^{-}}{\lim }$f(x) = $\underset{x\to 0^{-}}{\lim }$x = 0

Vậy f(x) gián đoạn tại x = 0.

Bài 3: Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 3 và $\underset{x\to 1}{\lim }$[2f(x)-g(x)] = 4. Tính g(1).

Hướng dẫn giải

Vì hàm số f(x) liên tục tại x = 1 nên hàm số 2f(x) cũng liên tục tại x = 1.

Mà hàm số g(x) liên tục tại x = 1. Do đó, hàm số y = 2f(x) – g(x) liên tục tại x = 1.

Suy ra: $\underset{x\to 1}{\lim }$[2f(x)-g(x)] = 2f(1) – g(1) = 4

Mà f(1) = 3 nên ta có: 2 . 3 – g(1) = 4, suy ra g(1) = 2.

Vậy g(1) = 2.

Bài 4. Tìm giá trị m để hàm số sau đây liên tục trên tập xác định:

Hướng dẫn giải

Tập xác định của hàm số là D = ℝ.

Xét trường hợp x ≠ 1, hàm số có dạng f(x) = $\frac{x^2-3x+2}{x-1}$, là hàm số phân thức trên tập xác định (–∞; 1) ∪ (1; +∞) nên nó liên tục trên các khoảng (–∞; 1) và (1; +∞).

Xét trường hợp x = 1, ta có:

• f(1) = 2m. 1+1= 2m +1

Khi đó, để hàm f (x) liên tục tại điểm x₀ = 1 thì:

$\underset{x\to 1}{\lim }$f(x) = f(1)$\iff$2m+1= -1$\iff$m = - 1

Vậy m = −1 là giá trị của tham số m cần tìm.

Bài 5. Xét tính liên tục của hàm số sau đây tại điểm x = 3.

Hướng dẫn giải

Ta có:

• $\underset{x\to 3^{+}}{\lim }$f(x) = $\underset{x\to 3^{+}}{\lim }$3 = 3

Do $\underset{x\to 3^{+}}{\lim }$f(x) $\ne$ $\underset{x\to 3^{-}}{\lim }$f(x) (3 $\ne$5) nên hàm số gián đoạn tại điểm x = 3.

Bài 6. Chứng minh rằng phương trình 3x³ + x² – x – 1 có nghiệm trong khoảng (−1; 1).

Hướng dẫn giải

Hàm số f(x) = 3x³ + x² – x – 1 là một hàm số đa thức, nên f (x) liên tục trên ℝ.

Suy ra, f (x) cũng liên tục trên đoạn [−1; 1].

Ta có:

• f(–1) = 3 . (–1)³ + (–1)² – (–1) – 1 = –3 + 1 + 1 – 1 = –2;

• f(1) = 3 . 1³ + 1² – 1 – 1 = 3 + 1 – 1 – 1 = 2.

Suy ra f(–1) . f(1) = (–2) . 2 = – 4 < 0.

Do vậy, có ít nhất một nghiệm c $\in$ (−1; 1) sao cho f (c) = 0.

Vậy phương trình 3x³ + x² – x – 1 có nghiệm trong khoảng (−1; 1).

Bài 7. Dùng định nghĩa xét tính liên tục của hàm số f(x) = x³ + 2x – 1 tại x₀ = –1.

Hướng dẫn giải

Vậy hàm số đã cho liên tục tại x₀ = –1.

Bài 8. Xét tính liên tục của các hàm số sau trên tập xác định của hàm số đó:

a) f(x) = x + sinx;

.

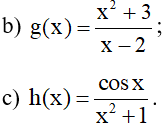
Hướng dẫn giải

a) Hàm số f(x) có tập xác định là ℝ.

Hai hàm số x và sinx liên tục trên ℝ nên hàm số f(x) = x + sinx liên tục trên ℝ.

b) Hàm số 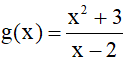 có tập xác định là ℝ\{2}.

Do đó hàm số 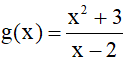 liên tục trên mỗi khoảng (–∞; 2) và (2; +∞).

c) Hàm số h(x) có tập xác định là ℝ.

Vì tử thức cosx liên tục ℝ và mẫu thức x² + 1 ≠ 0 liên tục trên ℝ.

Vậy h(x) liên tục trên ℝ.

Bài 9. Xét tính liêm tục của hàm số 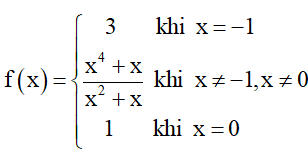  trên tập xác định của nó.

Hướng dẫn giải

Hàm số có TXĐ: D = ℝ.

Hàm số liên tục trên mỗi khoảng (–∞; –1); (–1; 0)  và (0; +∞).

• Tại x = –1, ta có:

⇒ Hàm số f(x) liên tục tại x = –1.

• Tại x = 0, ta có:

⇒ Hàm số f(x) liên tục tại x = 0.

Vậy hàm số f(x) liên tục tại mọi điểm x ∈ ℝ.

Bài 10. Tìm giá trị của tham số m để hàm số 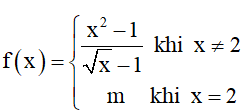 liên tục trên đoạn [0; 2].

Hướng dẫn giải

Hàm số xác định trên [0; 2] và liên tục trên [0; 2).

Khi đó để f(x) liên tục trên đoạn [0; 2] thì hàm số liên tục tại x = 2.

Tức là ta cần có: 

Ta có: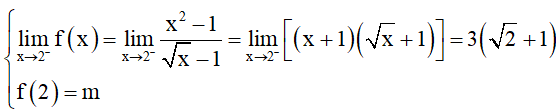     

Do đó (*) xảy ra khi và chỉ khi .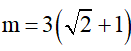

B. Lý thuyết Hàm số liên tục

1. Hàm số liên tục tại một điểm

Cho hàm số y = f(x) xác định trên khoảng K và x₀ $\in$ K.

Hàm số y = f(x) được gọi là liên tục tại điểm x₀ nếu$\underset{x\to x_0}{\lim }$f(x) = f(x₀) .

Nhận xét: Để hàm số y = f(x) liên tục tại x₀ thì phải có cả ba điều sau:

• Hàm số xác định tại x₀;

• Tồn tại $\underset{x\to x_0}{\lim }$f(x) ;

• $\underset{x\to x_0}{\lim }$ f(x) = f(x₀) .

Chú ý: Khi hàm số y = f(x) không liên tục tại điểm x₀ thì ta nói f (x) gián đoạn tại điểm  x₀ và x₀ được gọi là điểm gián đoạn của hàm số f (x).

Hướng dẫn giải

Ta có:

Vì $\underset{x\to 1^{+}}{\lim }$f(x) = $\underset{x\to 1^{-}}{\lim }$f(x) = f(1)nên hàm số trên liên tục tại điểm x = 1.

2. Hàm số liên tục trên một khoảng, trên một đoạn

• Cho hàm số y = f(x) xác định trên khoảng (a; b).

Hàm số y = f(x) được gọi là liên tục trên khoảng (a; b) nếu f(x) liên tục tại mọi điểm trong khoảng ấy.

• Cho hàm số y = f(x) xác định trên đoạn [a; b].

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu f(x) liên tục trên khoảng (a; b) và $\underset{x\to a^{+}}{\lim }$f(x) = f(a), $\underset{x\to b^{-}}{\lim }$f(x) = f(b).

Nhận xét: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0 thì luôn tồn tại ít nhất một điểm c $\in$ (a; b) sao cho f (c) = 0.

Ví dụ: Xét tính liên tục của hàm số $y=\sqrt{x+2}+\sqrt{2-x}$  trên [−2; 2].

Hướng dẫn giải

Với mọi  $x_0\in$(-2; 2), ta có:

Do đó f (x) liên tục tại mọi điểm $x_0\in$(-2; 2)

Ta lại có:

Vậy hàm số $y=\sqrt{x+2}+\sqrt{2-x}$  liên tục trên đoạn [−2; 2].

3. Tính liên tục của hàm số sơ cấp

• Hàm số đa thức y = P (x)  , các hàm số lượng giác y = sin x, y = cos x liên tục trên ℝ.

• Hàm số phân thức y = $\frac{P \left(x\right)}{Q \left(x\right)}$, hàm số căn thức y = $\sqrt{P\left(x\right)}$, các hàm số lượng giác $y=\tan x,y=\cot x$  liên tục trên các khoảng của tập xác định của chúng.

Trong đó P(x) và Q(x) là các đa thức.

Nhận xét: Hàm số thuộc những loại trên được gọi chung là hàm số sơ cấp.

Sau đây, khi nói xét tính liên tục của một hàm số mà không nói gì thêm thì ta xét tính liên tục của hàm số đó trên những khoảng xác định của nó.

Ví dụ: Xét tính liên tục của các hàm số sau:

a) y = 2x³ + 3x² – 2;

b) $y=\frac{x^2+x+1}{x-2}$ .

Hướng dẫn giải

a) y = 2x³ + 3x² – 2 là hàm số đa thức nên nó liên tục trên ℝ.

b) $y=\frac{x^2+x+1}{x-2}$  là hàm số phân thức, có tập xác định (–∞; 2) ∪ (2; +∞) nên nó liên tục trên các khoảng (–∞; 2) và (2; +∞).

4. Tổng, hiệu, tích, thương của hàm số liên tục

Cho hai hàm số số y = f(x) và y = g(x) liên tục tại điểm x₀. Khi đó:

• Các hàm số y = f(x) + g(x); y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀.

• Hàm số y = $\frac{f\left(x\right)}{g\left(x\right)}$ liên tục tại x₀ nếu g(x₀) ≠ 0.

Ví dụ: Xét tính liên tục của hàm số $y=\frac{x-2}{\sqrt{x-4}}$ .

Hướng dẫn giải

Tập xác định của hàm số: D = (4; +∞).

Các hàm số y = x – 2 và $y=\sqrt{x-4}$  liên tục tại mọi điểm x₀ ∈ D.

Do đó, hàm số $y=\frac{x-2}{\sqrt{x-4}}$  liên tục trên khoảng (4; +∞).

Video bài giảng Toán 11 Bài 17: Hàm số liên tục - Kết nối tri thức