Với giải Bài 4.13 trang 82 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 11: Hai đường thẳng song song giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 11: Hai đường thẳng song song
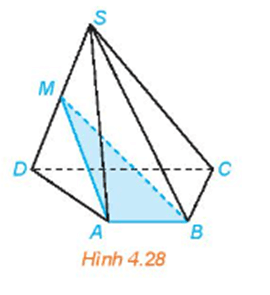
Bài 4.13 trang 82 Toán 11 Tập 1:Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).
a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
Lời giải:
a) Vì M thuộc SD nằm trong mặt phẳng (SCD) nên M thuộc mặt phẳng (SCD).
Mà M thuộc mặt phẳng (MAB) nên M là điểm chung của hai mặt phẳng (MAB) và (SCD).
Lại có hai mặt phẳng (MAB) và (SCD) chứa hai đường thẳng song song AB và CD.
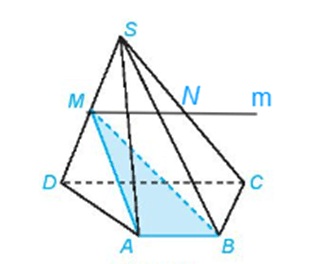
Do đó, giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng m đi qua M và song song với AB, CD.
b) Trong tam giác SCD, đường thẳng m đi qua điểm M và song song với CD cắt cạnh SC tại một điểm N.
Vì N thuộc m và m nằm trong mặt phẳng (MAB) nên N thuộc mặt phẳng (MAB).
Vậy N là giao điểm của đường thẳng SC và mặt phẳng (MAB).
Xét tam giác SCD có M là trung điểm của SD, MN // CD và N thuộc SC nên đường thẳng MN là đường trung bình của tam giác SCD
Sơ đồ tư duy Hai đường thẳng song song.

Video bài giảng Toán 11 Bài 11: Hai đường thẳng song song - Kết nối tri thức
Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Mở đầu trang 78 Toán 11 Tập 1: Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?...
HĐ1 trang 78 Toán 11 Tập 1: Quan sát bốn tuyến đường trong Hình 4.13 và trả lời các câu hỏi sau:...
Câu hỏi trang 79 Toán 11 Tập 1: Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.....
Luyện tập 1 trang 79 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17)....
Luyện tập 2 trang 80 Toán 11 Tập 1: Trong hình chóp tứ giác S.ABCD (H.4.19), chỉ ra những đường thẳng:...
Vận dụng 1 trang 80 Toán 11 Tập 1: Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?...
HĐ2 trang 80 Toán 11 Tập 1: Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.....
HĐ3 trang 80 Toán 11 Tập 1: Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?...
Luyện tập 3 trang 81 Toán 11 Tập 1: Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành....
HĐ4 trang 81 Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c.....
Luyện tập 4 trang 82 Toán 11 Tập 1: Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)....
Vận dụng 2 trang 82 Toán 11 Tập 1: Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bể nước....
Bài 4.9 trang 82 Toán 11 Tập 1: Trong không gian, cho ba đường thẳng a, b, c. Những mệnh đề nào sau đây là đúng?....
Bài 4.10 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?....
Bài 4.11 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành.....
Bài 4.12 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang....
Bài 4.13 trang 82 Toán 11 Tập 1:Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).....
Bài 4.14 trang 83 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC....
Bài 4.15 trang 83 Toán 11 Tập 1: (Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.....
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 10: Đường thẳng và mặt phẳng trong không gian
Bài 11: Hai đường thẳng song song
Bài 12: Đường thẳng và mặt phẳng song song
Bài 13: Hai mặt phẳng song song
Bài 14: Phép chiếu song song
