Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 11: Hai đường thẳng song song chi tiết sách Toán 11 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 11: Hai đường thẳng song song

Giải Toán 11 trang 78

Mở đầu trang 78 Toán 11 Tập 1: Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?

Lời giải:

Toán học mô tả vị trí tương quan giữa các tuyến đường trên như những đường thẳng chéo nhau.

1. Vị trí tương đối của hai đường thẳng

HĐ1 trang 78 Toán 11 Tập 1: Quan sát bốn tuyến đường trong Hình 4.13 và trả lời các câu hỏi sau:

a) Hai tuyến đường nào giao nhau?

b) Hai tuyến đường nào không giao nhau?

c) Hai tuyến đường nào song song?

Lời giải:

Quan sát Hình 4.13 ta thấy:

a) Hai tuyến đường mũi tên màu đỏ và mũi tên màu vàng giao nhau.

b) Hai tuyến đường mũi tên màu xanh dương và màu xanh lá cây không giao nhau.

c) Hai tuyến đường mũi tên màu xanh dương và mũi tên màu đỏ song song.

Giải Toán 11 trang 79 Tập 1

Câu hỏi trang 79 Toán 11 Tập 1: Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.

Lời giải:

+) Hình ảnh thực tế hai đường thẳng song song: hai cạnh đối diện chiếc bàn, các vạch kẻ đường, thanh lan can, …

+) Hình ảnh thực tế hai đường thẳng chéo nhau: cầu vượt và đường dưới, bóng đèn tuýp gắn trên tường và cạnh (không nằm trên tường treo đèn) của mặt tường bên cạnh,...

Luyện tập 1 trang 79 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17).

a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?

b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thẳng nào chéo nhau hay không?

Lời giải:

a) Hai đường thẳng AB và AC cắt nhau tại giao điểm A.

Hai đường thẳng AB và CD song song với nhau (do ABCD là hình bình hành).

Hai đường thẳng AC và CD cắt nhau tại giao điểm C.

b) Vì hai điểm M, N lần lượt là hai điểm thuộc hai cạnh SA, SB nên hai điểm M, N thuộc mặt phẳng (SAB) hay các điểm S, A, B, M, N cùng thuộc một mặt phẳng nên các đường thẳng SA, MN, AB đồng phẳng, do đó khi lấy bất kì 2 trong 3 đường thẳng trên thì chúng có thể cắt nhau hoặc song song hoặc trùng nhau. Vậy trong các đường thẳng SA, MN, AB, không có hai đường thẳng nào chéo nhau.

Giải Toán 11 trang 80 Tập 1

Luyện tập 2 trang 80 Toán 11 Tập 1: Trong hình chóp tứ giác S.ABCD (H.4.19), chỉ ra những đường thẳng:

a) Chéo với đường thẳng SA;

b) Chéo với đường thẳng BC.

Lời giải:

a) Các đường thẳng chéo với đường thẳng SA là BC và CD.

Giải thích: Nếu hai đường thẳng SA và BC không chéo nhau thì chúng cùng thuộc một mặt phẳng. Khi đó bốn điểm S, A, B, C đồng phẳng, trái với giả thiết S.ABCD là hình chóp. Do đó, hao đường thẳng SA và BC chéo nhau. Tương tự, giải thích được hai đường thẳng SA và CD chéo nhau.

b) Các đường thẳng chéo với đường thẳng BC là SA và SD. Giải thích tương tự câu a.

Vận dụng 1 trang 80 Toán 11 Tập 1: Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?

Lời giải:

Ta không thể đặt chiếc gậy đó song song với một trong các mép tường vì điểm đầu gậy chạm với sàn và 4 điểm góc của tường là các điểm không đồng phẳng nên đường thẳng tạo bởi chiếc gậy và một trong các mép tường là hai đường thẳng chéo nhau.

2. Tính chất của hai đường thẳng song song

HĐ2 trang 80 Toán 11 Tập 1: Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.

a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?

Lời giải:

a) Trên mặt phẳng (P) có một và chỉ một đường thẳng đi qua M và song song với d (theo tiên đề Euclid).

b) Giả sử x là đường thẳng đi qua M và song song với d. Khi đó hai đường thẳng x và d đồng phẳng. Mà điểm M và đường thẳng d đều cùng nằm trong mặt phẳng (P) nên x và d cùng nằm trong mặt phẳng (P).

Vậy nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó thuộc mặt phẳng (P).

HĐ3 trang 80 Toán 11 Tập 1: Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?

Lời giải:

Hai đường thẳng song song với mép trên của bảng, ta có thể chọn là mép trên của tường có gắn bảng và mép dưới của bảng liền với tường, hai đường thẳng này có song song với nhau.

Giải Toán 11 trang 81 Tập 1

Luyện tập 3 trang 81 Toán 11 Tập 1: Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.

Lời giải:

Ta có: EF // AB (do ABEF là hình bình hành) và CD // AB (do ABCD là hình bình hành).

Do đó, CD // EF.

Khi đó, hai đường thẳng CD và EF đồng phẳng hay bốn điểm C, D, E, F đồng phẳng.

Lại có EF = AB và CD = AB (do ABEF và ABCD là các hình bình hành) nên CD = EF.

Vậy tứ giác CDFE là hình bình hành.

HĐ4 trang 81 Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c.

a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.

b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.

Lời giải:

a) Vì M thuộc a nằm trong mặt phẳng (R) nên M thuộc mặt phẳng (R).

Vì M thuộc c nằm trong mặt phẳng (Q) nên M thuộc mặt phẳng (Q).

Do đó, M là một điểm chung của hai mặt phẳng (R) và (Q).

Lại có hai mặt phẳng (R) và (Q) có giao tuyến là đường thẳng b.

Vậy M thuộc b hay đường thẳng b đi qua điểm M.

b) Ta thấy ba đường thẳng phân biệt a, b, c đôi một đồng phẳng.

Do đó, nếu không có hai trong ba đường thẳng nào trong chúng cắt nhau thì a, b, c đôi một song song.

Vậy nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c song song với nhau.

Giải Toán 11 trang 82 Tập 1

Luyện tập 4 trang 82 Toán 11 Tập 1: Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).

Lời giải:

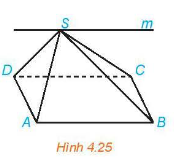
Hai mặt phẳng (SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song là AD và BC. Do đó, giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng n đi qua S và song song với AD, BC.

Vận dụng 2 trang 82 Toán 11 Tập 1: Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bể nước.

Lời giải:

Giả sử mặt phẳng (ABFE) mà mặt nước, mặt phẳng (EFCD) là mặt đáy của bể kính và (ABCD) là một mặt bên của bể kính.

Ba mặt phẳng (ABFE), (EFCD) và (ABCD) là ba mặt phẳng đôi một cắt nhau theo các giao tuyến EF, AB và CD. Vì DC // EF (do đáy của bể là hình chữ nhật) nên ba đường thẳng EF, AB và CD đôi một song song. Vậy đường mép nước AB song song với cạnh CD của bể nước.

Bài tập

Bài 4.9 trang 82 Toán 11 Tập 1: Trong không gian, cho ba đường thẳng a, b, c. Những mệnh đề nào sau đây là đúng?

a) Nếu a và b không cắt nhau thì a và b song song.

b) Nếu b và c chéo nhau thì b và c không cùng thuộc một mặt phẳng.

c) Nếu a và b cùng song song với c thì a song song với b.

d) Nếu a và b cắt nhau, b và c cắt nhau thì a và c cắt nhau.

Lời giải:

a) Mệnh đề a) là mệnh đề sai vì nếu a và b không cắt nhau thì a và b có thể song song hoặc chéo nhau.

b) Mệnh đề b) là mệnh đề đúng (theo định nghĩa hai đường thẳng chéo nhau).

c) Mệnh đề c) là mệnh đề sai vì hai đường thẳng a và b có thể trùng nhau.

d) Mệnh đề d) là mệnh đề sai vì a và c có thể cắt nhau hoặc chéo nhau hoặc song song hoặc trùng nhau.

Bài 4.10 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?

a) AB và CD;

b) AC và BD;

c) SB và CD.

Lời giải:

a) Hai đường thẳng AB và CD song song với nhau do đáy ABCD là hình bình hành.

b) Hai đường thẳng AC và BD cắt nhau do đây là hai đường chéo của hình bình hành ABCD.

c) Hai đường thẳng SB và CD chéo nhau.

Thật vậy, nếu hai đường thẳng SB và CD không chéo nhau, tức là hai đường thẳng này đồng phẳng hay bốn điểm S, B, C, D đồng phẳng, trái với giả thiết S.ABCD là hình chóp.

Bài 4.11 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành.

Lời giải:

Xét tam giác SAB có M và N lần lượt là trung điểm của các cạnh SA và SB nên MN là đường trung bình của tam giác SAB, suy ra MN // AB và MN = $\frac{1}{2}$ AB.

Tương tự ta có PQ là đường trung bình của tam giác SCD nên PQ // CD và PQ = $\frac{1}{2}$ CD.

Lại có đáy ABCD là hình bình hành nên AB // CD và AB = CD.

Khi đó, MN // PQ và MN = PQ. Vậy tứ giác MNPQ là hình bình hành.

Bài 4.12 trang 82 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.

Lời giải:

Xét tam giác SAB có M và N lần lượt là trung điểm của các cạnh SA và SB nên MN là đường trung bình của tam giác SAB, suy ra MN // AB.

Mà đáy ABCD là hình thang có AB // CD.

Do đó, MN // CD. Vậy tứ giác MCD là hình thang.

Bài 4.13 trang 82 Toán 11 Tập 1:Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).

a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).

b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.

Lời giải:

a) Vì M thuộc SD nằm trong mặt phẳng (SCD) nên M thuộc mặt phẳng (SCD).

Mà M thuộc mặt phẳng (MAB) nên M là điểm chung của hai mặt phẳng (MAB) và (SCD).

Lại có hai mặt phẳng (MAB) và (SCD) chứa hai đường thẳng song song AB và CD.

Do đó, giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng m đi qua M và song song với AB, CD.

b) Trong tam giác SCD, đường thẳng m đi qua điểm M và song song với CD cắt cạnh SC tại một điểm N.

Vì N thuộc m và m nằm trong mặt phẳng (MAB) nên N thuộc mặt phẳng (MAB).

Vậy N là giao điểm của đường thẳng SC và mặt phẳng (MAB).

Xét tam giác SCD có M là trung điểm của SD, MN // CD và N thuộc SC nên đường thẳng MN là đường trung bình của tam giác SCD.

Giải Toán 11 trang 83 Tập 1

Bài 4.14 trang 83 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD và P là một điểm thuộc cạnh AC.

a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (BPD).

b) Chứng minh rằng d song song với BD.

Lời giải:

a) Trong tam giác ABC, gọi giao điểm của hai đường thẳng BP và AM là E.

Trong tam giác ACD, gọi giao điểm của hai đường thẳng DP và AN là F.

Vì E thuộc AM nên E thuộc mặt phẳng (AMN), vì F thuộc AN nên F thuộc mặt phẳng (AMN), do đó đường thẳng EF nằm trong mặt phẳng (AMN).

Vì E thuộc BP nên E thuộc mặt phẳng (BPD), vì F thuộc DP nên F thuộc mặt phẳng (BPD), do đó đường thẳng EF nằm trong mặt phẳng (BPD).

Vậy đường thẳng EF là giao tuyến của hai mặt phẳng (AMN) và (BPD) hay đường thẳng d cần tìm chính là đường thẳng EF.

b) Xét tam giác BCD có M, N lần lượt là trung điểm của các cạnh BC, CD nên MN là đường trung bình của tam giác BCD, do đó MN // BD.

Hai mặt phẳng (AMN) và (BPD) có chứa hai đường thẳng song song là MN và BD. Do đó, giao tuyến d của hai mặt phẳng (AMN) và (BPD) song song với MN và BD.

Vậy d // BD.

Bài 4.15 trang 83 Toán 11 Tập 1: (Đố vui) Khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau (H.4.29). Hãy giải thích tại sao.

Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau hay không?

Lời giải:

+) Mỗi cánh cửa ở Hình 4.29 đều có dạng hình chữ nhật nên các cạnh đối diện của mỗi cánh cửa song song với nhau.

Khi đó ta có a // b và c // d.

Lại có các đường thẳng a và d là đường thẳng giao tuyến giữa khung cửa và cánh cửa nên a // d.

Do vậy, bốn đường thẳng a, b, c, d luôn đôi một song song với nhau.

Vậy khi hai cánh cửa sổ hình chữ nhật được mở, dù ở vị trí nào, thì hai mép ngoài của chúng luôn song song với nhau.

+) Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30 thì không có vị trí nào của hai cánh cửa để hai mép ngoài của chúng song song với nhau.

Video bài giảng Toán 11 Bài 11: Hai đường thẳng song song - Kết nối tri thức

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 10: Đường thẳng và mặt phẳng trong không gian

Bài 11: Hai đường thẳng song song

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Lý thuyết Hai đường thẳng song song

1. Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng a, b trong không gian.

• Nếu a và b cùng nằm trong một mặt phẳng thì ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau.
• Nếu a và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói a và b chéo nhau. Khi đó, ta cũng nói a chéo với b hoặc b chéo với a.

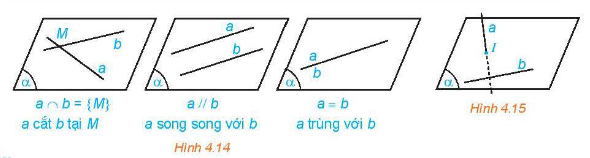
2. Tính chất của hai đường thẳng song song

Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.

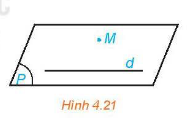
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.

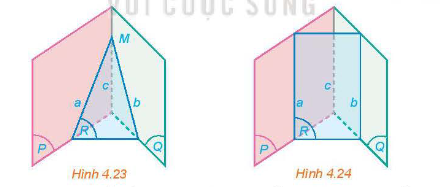
* Chú ý: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

VD: $\left(SAB\right)\cap \left(SBC\right)=Sm$