Với giải sách bài tập Toán 11 Bài 11: Hai đường thẳng song song sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 11: Hai đường thẳng song song

Giải SBT Toán 11 trang 59

Bài 4.13 trang 59 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau:

a, Đường thẳng NP song song với đường thẳng BD.

b, Đường thẳng NP cắt BD.

Lời giải:

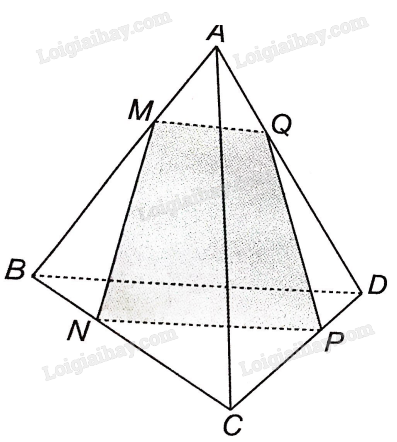
a,

NP là giao tuyến của hai mặt phẳng (MNP và (BCD

BD là giao tuyến của hai mặt phẳng (ABD và (BCD

Mà NP // BD nên giao tuyến của (MNP và (ABD cũng là một đường thẳng song song với NP và BD.

Ta thấy M thuộc AB nên M là điểm chung của (MNP và (ABD.

Vậy giao tuyến của (MNP và (ABD là đường thẳng d đi qua M, song song với NP và BD.

Trong mặt phẳng (ABD, gọi Q là giao điểm giữa d và AD.

Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP chính là điểm Q.

b,

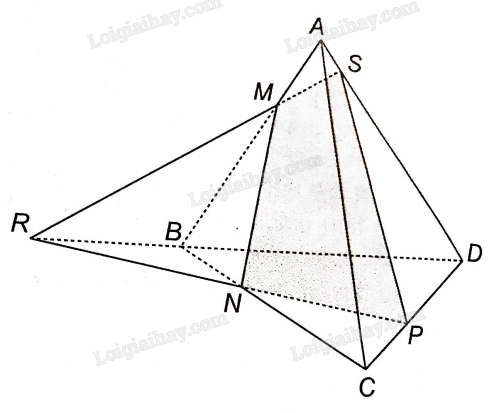
NP là giao tuyến của hai mặt phẳng (MNP) và (BCD)

BD là giao tuyến của hai mặt phẳng (ABD) và (BCD)

Mà đường thẳng NP và BD cắt nhau nên giao tuyến d của (MNP) và (ABD) là một đường thẳng đồng quy với NP và BD. (gọi R là giao điểm của NP và BD, vậy d đi qua điểm R

Ta thấy M thuộc AB nên M là điểm chung của (MNP) và (ABD). Vậy M thuộc đường giao tuyến d.

Trong mặt phẳng (BCD) gọi S là giao điểm của MR và BD, vậy giao tuyến d cũng sẽ đi qua điểm S.

Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) chính là điểm S.

Bài 4.14 trang 59 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là một điểm bất kì thuộc cạnh SC.

a, Xác định các giao tuyến của mặt phẳng (MAB với các mặt của hình chóp.

b, Xác định các giao tuyến của mặt phẳng (MAD với các mặt của hình chóp.

Lời giải:

a,

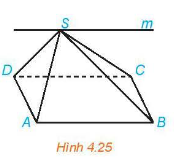
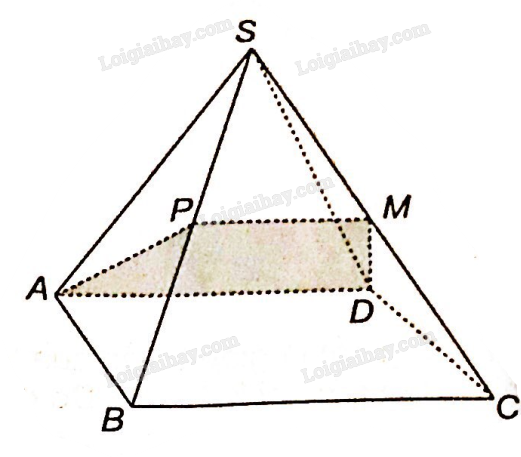
Xét ba mặt phẳng (MAB, (SCD và (ABCD

AB là giao tuyến của (MAB và (ABCD

CD là giao tuyến của (SCD và (ABCD

Mà AB//CD (hình bình hành ABCD nên giao tuyến của (MAB và (SCD cũng song song với AB và CD.

Ta thấy M thuộc SC nên M là một điểm chung của (MAB và (SCD. Vậy giao tuyến sẽ là đường thẳng qua M, song song với AB, CD.

Vẽ MN//CD trong mặt phẳng (SCD.

Ta thấy giao tuyến của (MAB và các mặt của chóp lần lượt là MN, NA, AB, MB.

b,

Xét ba mặt phẳng (MAD), (SBC và (ABCD)

AD là giao tuyến của (MAD) và (ABCD)

CB là giao tuyến của (SBC) và (ABCD)

Mà AD//CB (hình bình hành ABCD nên giao tuyến của (MAD và (SBC cũng song song với AD và CB.

Ta thấy M thuộc SC nên M là một điểm chung của (MAD và (SBC). Vậy giao tuyến sẽ là đường thẳng qua M, song song với AD, CB.

Vẽ MP//CB trong mặt phẳng (SCB)

Ta thấy giao tuyến của (MAD) và các mặt của chóp lần lượt là MP, PA, AB, MB.

Bài 4.15 trang 59 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi M, N lần lượt là các điểm thuộc các cạnh SA, SD.

a) Xác định giao tuyến d của hai mặt phẳng (MCD) và (NAB).

b) Chứng minh rằng d // AB.

Lời giải:

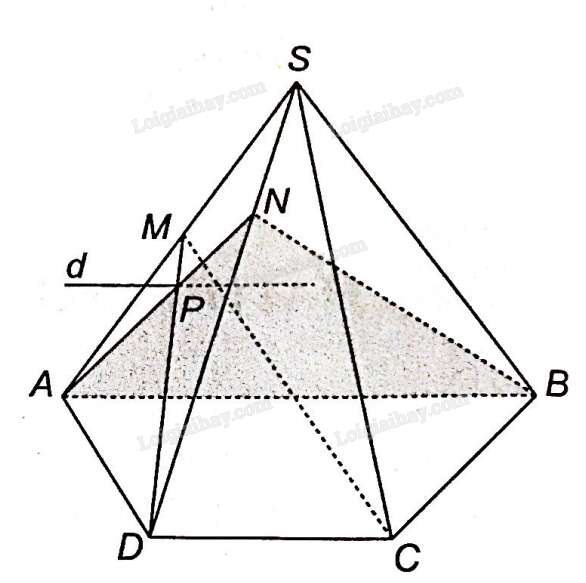
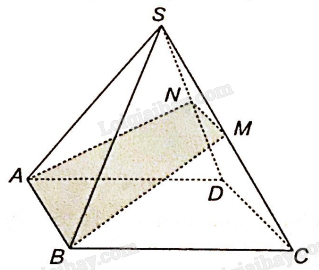
a) Xét ba mặt phẳng (MCD), (NAB) và (ABCD)

CD là giao tuyến của (MCD) và (ABCD)

AB là giao tuyến của (NAB) và (ABCD)

Mà AB//CD nên giao tuyến d của (MCD) và (NAB) cũng song song với AB và CD.

Gọi P là giao điểm của MD và NA trên mặt phẳng (SAD), vậy P là một điểm chung của (MCD) và (NAB). Vậy giao tuyến d sẽ là đường thẳng qua P, song song với AB, CD.

b) Vậy d // AB.

Bài 4.16 trang 59 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Xác định giao tuyến của hai mặt phẳng (ANP) và (CMQ).

b) Xác định giao tuyến của hai mặt phẳng (ANP) và (ABD).

c) Xác định giao tuyến của hai mặt phẳng (CMQ) và (BCD).

d) Chứng minh rằng các giao tuyến ở trên đôi một song song với nhau.

Lời giải:

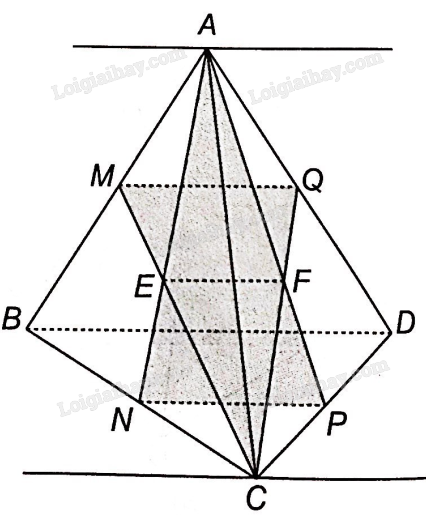
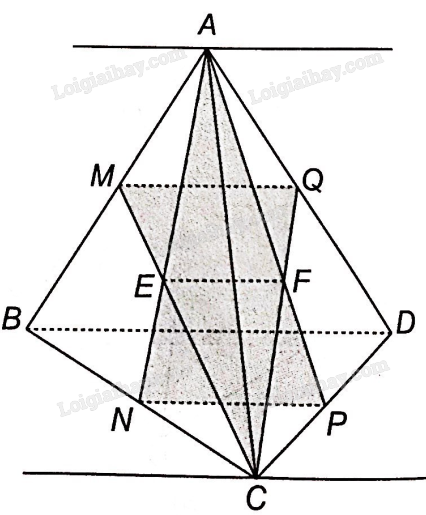
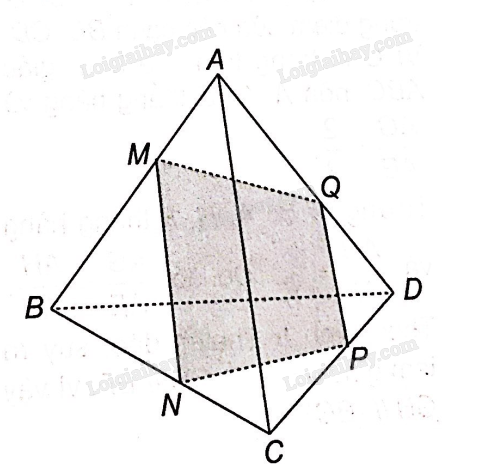
a) M, Q lần lượt là trung điểm của các cạnh AB, DA nên MQ là đường trung bình tam giác ABD nên MQ//BD.

N, P lần lượt là trung điểm của các cạnh BC, CD nên NP là đường trung bình tam giác CBD nên NP//BD.

Vậy MQ//NP, suy ra M, N, P, Q đồng phẳng.

Xét 3 mặt phẳng (MNPQ), (ANP) và (CMQ).

MQ là giao tuyến của (MNPQ) và (CMQ).

NP là giao tuyến của (MNPQ) và (ANP).

Vậy giao tuyến của (ANP) và (CMQ) cũng là một đường thẳng song song với MQ và NP.

Trong mặt phẳng (ABC), gọi E là giao điểm của AN và MC. Trong mặt phẳng (ACD) gọi F là giao điểm của CQ và AP. Vậy EF là giao tuyến của hai mặt phẳng (ANP) và (CMQ).

b)

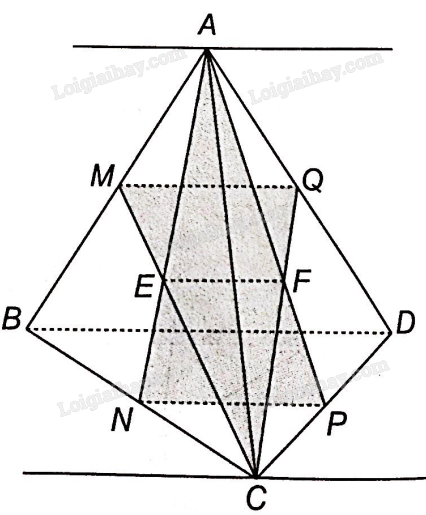
Xét 3 mặt phẳng (BCD), (ANP) và (ABD).

BD là giao tuyến của (BCD) và (ABD).

NP là giao tuyến của (BCD) và (ANP).

Mà theo chứng minh trên, BD//NP.

Vậy giao tuyến của (ANP) và (ABD) cũng là một đường thẳng song song với BD và NP.

Mà A là điểm chung của hai mặt phẳng (ANP) và (ABD) , vậy giao tuyến của hai mặt phẳng đó là đường thẳng đi qua A và song song với BD.

c)

Xét 3 mặt phẳng (BCD), (ABD) và (CMQ).

MQ là giao tuyến của (ABD) và (CMQ).

BD là giao tuyến của (BCD) và (ABD).

Mà MQ//BD nên giao tuyến của mặt phẳng (CMQ) và (BCD) cũng là một đường thẳng song song với MQ và BD.

Ta thấy C là một điểm chung của mặt phẳng (CMQ) và (BCD), vậy giao tuyến của hai mặt phẳng (CMQ) và (BCD) là đường thẳng đi qua C và song song với BD.

d) Theo chứng minh trên, các đường giao tuyến đều song song với MQ, NP, BD nên chúng song song với nhau.

Bài 4.17 trang 59 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song.

Lời giải:

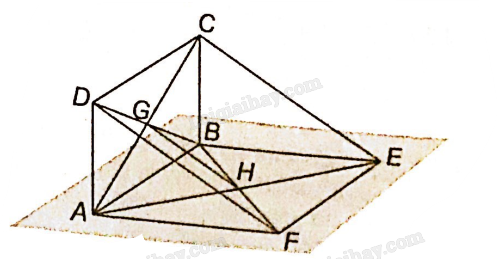
G là giao điểm hai đường chéo BD, AC của hình bình hành ABCD nên G là trung điểm của BD và AC.

H là giao điểm hai đường chéo BF, AE của hình bình hành ABEF nên H là trung điểm của BF và AE.

Xét tam giác BDF, GH là đường trung bình của tam giác nên GH song song với DF.

GH là đường trung bình tam giác ACE nên GH song song với CE.

Vậy ba đường thẳng GH, CE, DF đôi một song song.

Bài 4.18 trang 59 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi E, F lần lượt là trọng tâm của các tam giác SAD, SBC.

a) Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Chứng minh rằng EF//MN, từ đó suy ra EF//AB.

b) Xác định các giao tuyến của mặt phẳng (AEF) với các mặt của hình chóp.

c) Trong các giao tuyến tìm được ở câu b, giao tuyến nào song song với đường thẳng EF?

Lời giải:

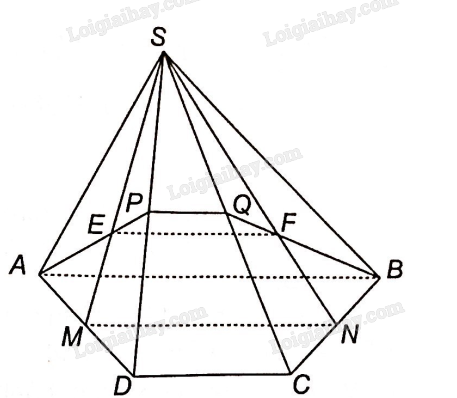
a) E là trọng tâm tam giác SAD nên SE = 2EM.

F là trọng tâm tam giác SBC nên SF = 2FN.

Xét tam giác SMN, ta có tỉ số $\frac{\mathrm{S}\mathrm{E}}{\mathrm{S}\mathrm{F}}=\frac{2\mathrm{E}\mathrm{M}}{2\mathrm{F}\mathrm{N}}=\frac{\mathrm{E}\mathrm{M}}{\mathrm{F}\mathrm{N}}$ nên EF//MN

M, N lần lượt là trung điểm của các cạnh AD, BC nên MN là đường trung bình hình thang ABCD. Suy ra MN//AB. Suy ra EF//AB.

b) Trong mặt phẳng (SAD), gọi P là giao điểm của AE và SD

Trong mặt phẳng (SCD), gọi Q là giao điểm của BF và SC.

Giao tuyến của AE với các mặt của hình chóp lần lượt là: AP, PQ, QB, AB.

c) Trong các giao tuyến tìm được ở câu b, có AB và PQ song song với EF.

Xét 3 mặt phẳng (APQB), (SCD) và (ABCD). Ta thấy giao tuyến AB và CD song song. Vậy giao tuyến PQ cũng sẽ song song với AB và CD. Mà AB//EF nên PQ cũng song song với EF.

Giải SBT Toán 11 trang 60

Bài 4.19 trang 60 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Một mặt phẳng cắt bốn cạnh AB, BC, CD, DA lần lượt tại các điểm M, N, P, Q.

a) Chứng minh rằng các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.

b) Chứng minh rằng các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.

Lời giải:

a)

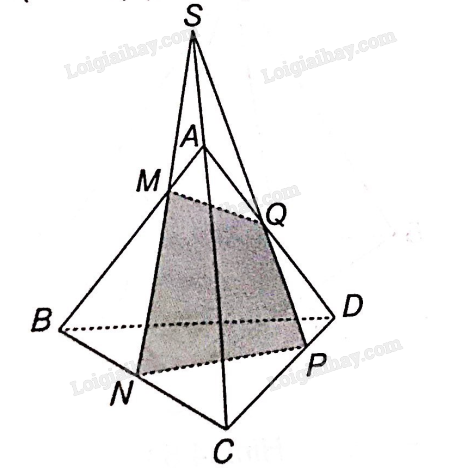
Xét 3 mặt phẳng (ABC), (ACD) và (MNPQ)

MN là giao tuyến của (MNPQ) và (ABC)

PQ là giao tuyến của (MNPQ) và (ACD)

AC là giao tuyến của (ABC) và (ACD).

Vậy, theo tính chất 3 giao tuyến của 3 mặt phẳng cắt nhau thì các đường thẳng MN, PQ, AC đôi một song song hoặc đồng quy.

b)

Xét 3 mặt phẳng (ABD), (BCD) và (MNPQ)

MQ là giao tuyến của (MNPQ) và (ABD)

NP là giao tuyến của (MNPQ) và (BCD)

BD là giao tuyến của (ABD) và (BCD).

Vậy, theo tính chất 3 giao tuyến của 3 mặt phẳng cắt nhau thì các đường thẳng MQ, NP, BD đôi một song song hoặc đồng quy.

Bài 4.20 trang 60 SBT Toán 11 Tập 1: Một chiếc thang được đặt sao cho hai đầu của chân thang dựa vào tường, hai đầu còn lại nằm trên sàn nhà (H. 4.12). Biết rằng chiếc thang có dạng hình chữ nhật, hãy giải thích vì sao hai đầu của chân thang nằm trên sàn nhà lại cách đều chân tường.

Lời giải:

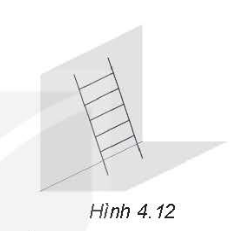
Áp dụng định lý ba đường giao tuyến của ba mặt phẳng: mặt phẳng sàn nhà, mặt chân tường à mặt phẳng tạo bởi bốn đầu của chân thang trên sàn nhà song song với đường thẳng chân tường.

Bài 4.21 trang 60 SBT Toán 11 Tập 1: Bạn Hà lấy một tờ giấy hình chữ nhật và gấp tờ giấy sao cho hai mép của tờ giấy song song với nhau (H.4.13). Hà thấy rằng dù gấp thế nào thì đường nếp gấp vẫn luôn song song với hai mép của tờ giấy. Hãy giải thích vì sao.

Lời giải:

Hai nửa của tờ giấy có thể coi như hai mặt phẳng chứa hai đường thẳng song song là hai mép giấy. Đường nếp gấy chính là giao tuyến của hai mặt phẳng này nên nó song song với mép giấy.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 10: Đường thẳng và mặt phẳng trong không gian

Bài 11: Hai đường thẳng song song

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Lý thuyết Hai đường thẳng song song

1. Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng a, b trong không gian.

• Nếu a và b cùng nằm trong một mặt phẳng thì ta nói a và b đồng phẳng. Khi đó, a và b có thể cắt nhau, song song với nhau hoặc trùng nhau.
• Nếu a và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói a và b chéo nhau. Khi đó, ta cũng nói a chéo với b hoặc b chéo với a.

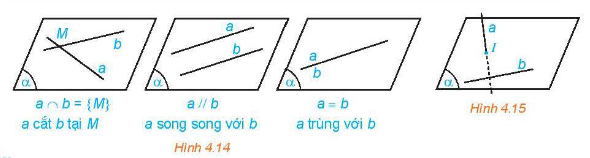
2. Tính chất của hai đường thẳng song song

Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.

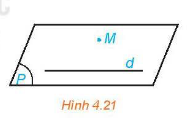
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì song song với nhau.

Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì 3 giao tuyến đó đồng quy hoặc đôi một song song.

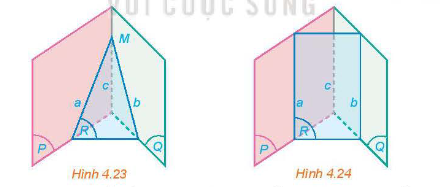
* Chú ý: Nếu hai mặt phẳng chứa 2 đường thẳng song song với nhau thì giao tuyến (nếu có) của chúng song song với 2 đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

VD: $\left(SAB\right)\cap \left(SBC\right)=Sm$