Giải Toán 11 trang 23 Tập 1 Chân trời sáng tạo

Giải Toán 11 trang 23 Tập 1 Chân trời sáng tạo

Nguyễn Mạnh Tài Ngày: 17-10-2023 Lớp 11

216

Với lời giải Toán 11 trang 23 Tập 1 chi tiết trong Bài 3: Các công thức lượng giác sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 3: Các công thức lượng giác

Thực hành 4 trang 23 Toán 11 Tập 1: Tính cos $\frac{7 π}{12}$ + cos $\frac{π}{12}$ .

Lời giải:

Thực hành 4 trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vận dụng trang 23 Toán 11 Tập 1: Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Vận dụng trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Lời giải:

Ta có: OA = OB = $\frac{120}{2}$ = 60 cm.

Xét tam giác OBB’ vuông tại B’, có:

$\sin \hat{B O B'} = \frac{B B'}{O B} = \frac{27}{60} = \frac{9}{20}$ .

$\Rightarrow cos \hat{B O B'} = \sqrt{1 - {(\frac{9}{20})}^{2}} = \frac{\sqrt{319}}{20}$

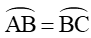
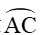
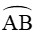
Vì Vận dụng trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11 nên sđ = 2.sđ $\Rightarrow \hat{A O C} = 2 \hat{B O B'}$

Xét tam giác OCC’ vuông tại C’, có:

Vận dụng trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Sau bài học này ta sẽ giải quyết tiếp được bài toán như sau:

Vận dụng trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vậy khoảng cách này từ điểm C đến AH là $60. \frac{9 \sqrt{319}}{200} \approx$ 48,2 (cm).

Bài tập

Bài 1 trang 23 Toán 11 Tập 1: Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:

a) $\frac{5 π}{12}$ ;

b) – 555°.

Lời giải:

a) Ta có:

Bài 1 trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

b) Ta có:

– 555° = $\frac{π . (- 555 °)}{180 °} = - \frac{37 π}{12} = - (3 π + \frac{π}{12})$ rad.

Khi đó:

Bài 1 trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Bài 2 trang 23 Toán 11 Tập 1: Tính $\sin (α + \frac{π}{6}), cos (\frac{π}{4} - α)$ biết sin $α = - \frac{5}{13}$ và $π < α < \frac{3 π}{2}$ .

Lời giải:

Ta có: cos $α = - \sqrt{1 - {(- \frac{5}{13})}^{2}} = - \frac{12}{13}$ (vì $π < α < \frac{3 π}{2}$ ).

Ta lại có:

Bài 2 trang 23 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Video bài giảng Toán 11 Bài 3: Các công thức lượng giác - Chân trời sáng tạo

Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 20 Toán 11 Tập 1: Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?...

Hoạt động khám phá 1 trang 21 Toán 11 Tập 1: Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ $\vec{O M}$ và $\vec{O N}$ sau đây:...

Thực hành 1 trang 21 Toán 11 Tập 1: Tính sin $\frac{π}{12}$ và tan $\frac{π}{12}$ ...

Hoạt động khám phá 2 trang 21 Toán 11 Tập 1: Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α...

Thực hành 2 trang 22 Toán 11 Tập 1: Tính cos và tan...

Hoạt động khám phá 3 trang 22 Toán 11 Tập 1: Từ công thức cộng, hãy tính tổng và hiệu của:...

Thực hành 3 trang 22 Toán 11 Tập 1: Tính giá trị của các biểu thức sin $\frac{π}{24}$ cos $\frac{5 π}{24}$ và sin $\frac{7 π}{8}$ sin $\frac{5 π}{8}$ ...

Hoạt động khám phá 4 trang 22 Toán 11 Tập 1: Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác $a = \frac{α + β}{2}$ và $b = \frac{α - β}{2}$ ta được các đẳng thức nào?...

Thực hành 4 trang 23 Toán 11 Tập 1: Tính cos $\frac{7 π}{12}$ + cos $\frac{π}{12}$ ...

Vận dụng trang 23 Toán 11 Tập 1: Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười...

Bài 1 trang 23 Toán 11 Tập 1: Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:...

Bài 2 trang 23 Toán 11 Tập 1: Tính $\sin (α + \frac{π}{6}), cos (\frac{π}{4} - α)$ biết sin $α = - \frac{5}{13}$ và $π < α < \frac{3 π}{2}$ ...

Bài 3 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc 2α, biết:...

Bài 4 trang 24 Toán 11 Tập 1: Rút gọn các biểu thức sau:...

Bài 5 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, biết:...

Bài 6 trang 24 Toán 11 Tập 1: Chứng minh rằng tam giác ABC, ta có sinA = sinB.cosC + sinC.cosB...

Bài 7 trang 24 Toán 11 Tập 1: Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn . Tính tan, từ đó tính độ dài cạnh CD...

Bài 8 trang 24 Toán 11 Tập 1: Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi $α = \frac{π}{2}$ và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA...

Bài 9 trang 24 Toán 11 Tập 1: Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là $\frac{2 π}{3}$ và số đo góc (OA, OM) là α...

Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

137

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.