HĐ2 trang 36 Toán lớp 10: Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa $\sin \alpha$ và $\sin \left({180}^o-\alpha \right)$, giữa $\cos \alpha$ và  $\cos \left({180}^o-\alpha \right)$.

Phương pháp giải:

Nhận xét vị trí của M và M’ trong mỗi trường hợp: $\alpha ={90}^o;\alpha <{90}^o;\alpha >{90}^o.$

Khi $0^o<\alpha <{90}^o$: $\cos \alpha ,\sin \alpha$ tương ứng là hoành độ và tung độ của điểm M.

Lời giải:

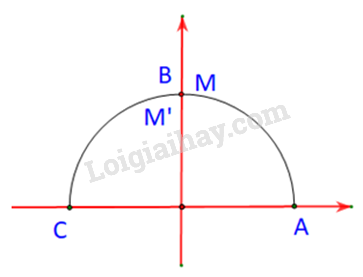
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc $\alpha$ và ${180}^o-\alpha$.

Giả sử $M\left(x_0;y_o\right)$. Khi đó $\cos \alpha =x_0;\sin \alpha =y_o$

Trường hợp 1:  $\alpha ={90}^o$

Khi đó $\alpha ={180}^o-\alpha ={90}^o$

Tức là M và M’ lần lượt trùng nhau và trùng với B.

Và  $\{\begin{array}{l}\cos \alpha =-\cos \left({180}^o-\alpha \right)=0;\\ \sin \alpha =\sin \left({180}^o-\alpha \right)=\sin {90}^o=1.\\ \cot \alpha =0\end{array}$

Không tồn tại $\tan \alpha$ với $\alpha ={90}^o$

Trường hợp 2: $\alpha <{90}^o\Rightarrow {180}^o-\alpha >{90}^o$

M nằm bên phải trục tung

M’ nằm bên trái trục tung

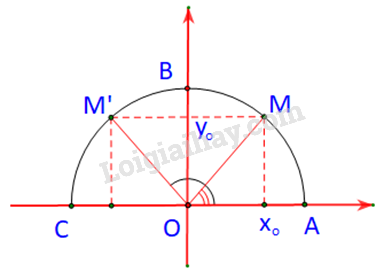
Dễ thấy: $\widehat{M^{\prime }OC}={180}^o-\widehat{xO{M}^{\prime }}={180}^o-\left({180}^o-\alpha \right)=\alpha =\widehat{xOM}$

$\Rightarrow \widehat{M^{\prime }OB}={90}^o-\widehat{M^{\prime }OC}={90}^o-\widehat{MOA}=\widehat{MOB}$

Xét tam giác $M^{\prime }OB$ và tam giác $MOB$  ta có:

$OM=O{M}^{\prime }$

$\widehat{M^{\prime }OB}=\widehat{MOB}$

OB chung

$\begin{array}{l}\Rightarrow \mathrm{\Delta }MOB=\mathrm{\Delta }{M}^{\prime }OB\\ \Rightarrow \{\begin{array}{l}OM=O{M}^{\prime }\\ BM=B{M}^{\prime }\end{array}\end{array}$

Hay OB là trung trực của đoạn thẳng MM’.

Nói cách khác M và M’ đối xứng với nhau qua trục tung.

Mà $M\left(x_0;y_o\right)$ nên $M^{\prime }\left(-x_0;y_o\right)$

$\begin{array}{l}\cos \left({180}^o-\alpha \right)=-x_0=-\cos \alpha ;\\ \sin \left({180}^o-\alpha \right)=y_o=\sin \alpha .\\ \Rightarrow \{\begin{array}{l}\tan \left({180}^o-\alpha \right)=-\tan \alpha \\ \cot \left({180}^o-\alpha \right)=-\cot \alpha \end{array}\end{array}$

Trường hợp 3: $\alpha >{90}^o\Rightarrow {180}^o-\alpha <{90}^o$

Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.

Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.

Như vậy

$\begin{array}{l}\cos \left({180}^o-\alpha \right)=-x_0=-\cos \alpha ;\\ \sin \left({180}^o-\alpha \right)=y_o=\sin \alpha .\\ \Rightarrow \{\begin{array}{l}\tan \left({180}^o-\alpha \right)=-\tan \alpha \\ \cot \left({180}^o-\alpha \right)=-\cot \alpha \end{array}\end{array}$

Kết luận: Với mọi $0^o<\alpha <{180}^o$, ta luôn có

$\begin{array}{l}\cos \left({180}^o-\alpha \right)=-\cos \alpha ;\\ \sin \left({180}^o-\alpha \right)=\sin \alpha .\\ \tan \left({180}^o-\alpha \right)=-\tan \alpha (\alpha \ne {90}^o)\\ \cot \left({180}^o-\alpha \right)=-\cot \alpha \end{array}$

Luyện tập 2 trang 36 Toán lớp 10: Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau $\alpha$ và ${90}^o-\alpha$ ($\widehat{xOM}=\alpha ,\widehat{xON}={90}^o-\alpha$). Chứng mình rằng $\mathrm{\Delta }MOP=\mathrm{\Delta }NOQ$. Từ đó nêu mối quan hệ giữa $\cos \alpha$ và $\sin \left({90}^o-\alpha \right)$.

Phương pháp giải:

Nhận xét vị trí của M và N trong mỗi trường hợp: $\alpha ={90}^o;\alpha <{90}^o$

Khi $0^o<\alpha <{90}^o$: $\cos \alpha ,\sin \alpha$ tương ứng là hoành độ và tung độ của điểm M.

Lời giải:

Trường hợp 1:  $\alpha ={90}^o$

Khi đó ${90}^o-\alpha =0^o$

Tức là M và N lần lượt trùng nhau với B và A.

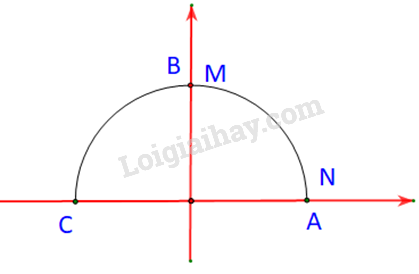
Và  $\cos \alpha =0=\sin \left({90}^o-\alpha \right)$

Trường hợp 2: $0^o<\alpha <{90}^o\Rightarrow 0^o<{90}^o-\alpha <{90}^0$

M và N cùng nằm bên trái phải trục tung.

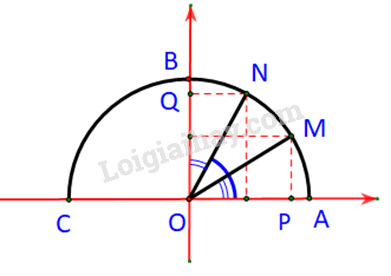
Ta có: $\alpha =\widehat{AOM};{90}^o-\alpha =\widehat{AON}$

Dễ thấy: $\widehat{AON}={90}^o-\alpha ={90}^o-\widehat{NOB}\Rightarrow \alpha =\widehat{NOB}$

Xét hai tam giác vuông $NOQ$ và tam giác $MOP$  ta có:

$OM=ON$

$\widehat{POM}=\widehat{QON}$

$\begin{array}{l}\Rightarrow \mathrm{\Delta }NOQ=\mathrm{\Delta }MOP\\ \Rightarrow \{\begin{array}{l}OP=OQ\\ QN=MP\end{array}\end{array}$

Mà $M\left(x_0;y_o\right)$ nên $N\left(y_o;x_0\right)$. Nói cách khác:

$\cos \left({90}^o-\alpha \right)=\sin \alpha ;\sin \left({90}^o-\alpha \right)=\cos \alpha .$

Xem thêm lời giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải Toán 10 trang 33 Tập 1 

Giải Toán 10 trang 34 Tập 1 

Giải Toán 10 trang 36 Tập 1 

Giải Toán 10 trang 37 Tập 1