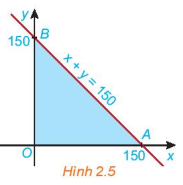
HĐ2 trang 28 Toán lớp 10: Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
a) Xác định miền nghiệm của các bất phương trình tương ứng và .
b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền và hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
Phương pháp giải:
a) Biểu diễn các miền nghiệm của từng bất phương trình và
Bước 1: Vẽ đường thẳng (nét liền) .
Bước 2: Lấy điểm một điểm không thuộc đường thẳng và thay vào bất phương trình cần xác định miền nghiệm.
Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.
b) Vẽ tất cả các miền miền và lên cùng một mặt phẳng.
Lời giải:
a)
Miền nghiệm của bất phương trình
Bước 1: Vẽ đường thẳng (nét liền) . Đây là trục Oy.
Bước 2: Lấy điểm A(150;0) không thuộc trục Oy và thay vào biểu thức , ta được: .
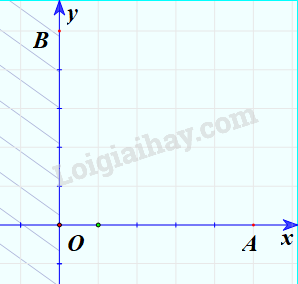
Bước 3: Do điểm A thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm A.
Minh họa (phần không bị gạch chéo):
Miền nghiệm của bất phương trình
Bước 1: Vẽ đường thẳng (nét liền) . Đây là trục Ox.
Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức , ta được: .
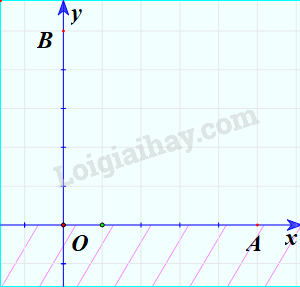
Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.
Minh họa (phần không bị gạch chéo):
Miền nghiệm của bất phương trình
Bước 1: Vẽ đường thẳng (nét liền) . Đây là trục Ox.
Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức , ta được: .
Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.
Minh họa (phần không bị gạch chéo):
Miền nghiệm của bất phương trình :
Bước 1: Vẽ đường thẳng (nét liền) .
Bước 2: Lấy điểm O(0;0) không thuộc đường thẳng và thay vào , ta được:
Bước 3: Do điểm O thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm O.
Minh họa (phần không bị gạch chéo):
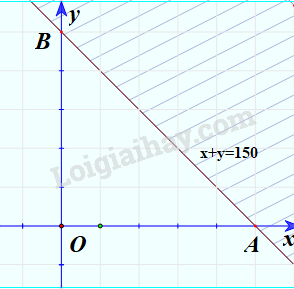
Vậy là nửa trên mặt phẳng có bờ là trục Oy, là nửa bên phải mặt phẳng có bờ là trục Ox và là nửa mặt phẳng có bờ là đường thẳng x+y=150 chứa điểm O.
b) Vẽ tất cả các miền miền và lên cùng một mặt phẳng.
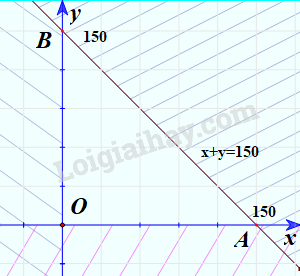
=>Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền và
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
Lấy điểm (1;2) trong tam giác OAB, thay vào hệ
Ta được:
(luôn đúng)
Vậy điểm (1;2) là nghiệm của hệ bất phương trình
Lấy điểm (1;149), thay vào hệ
Ta được:
(luôn đúng)
Vậy điểm (1;149) là nghiệm của hệ bất phương trình
Luyện tập 2 trang 28 Toán lớp 10: Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
Phương pháp giải:
Bước 1: Xác định miền nghiệm của bất phương trình
Bước 2: Xác định miền nghiệm của bất phương trình
Bước 3: Xác định miền nghiệm của bất phương trình
Bước 4: Xác định miền nghiệm của bất phương trình
Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
Lời giải:
Bước 1: Xác định miền nghiệm của bất phương trình
Miền nghiệm của bất phương trình là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Bước 2: Xác định miền nghiệm của bất phương trình
Miền nghiệm của bất phương trình là nửa mặt phẳng bờ Ox chứa điểm (0;1) không kể trục Ox.
Bước 3: Xác định miền nghiệm của bất phương trình
+ Vẽ đường thẳng d: x+y=100
+ Vì 0+0=0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Bước 4: Xác định miền nghiệm của bất phương trình
Tương tự miền nghiệm của bất phương trình là nửa mặt phẳng bờ d’ chúa gốc tọa độ O. (không kể đường thẳng d’).
Khi đó miền không bị gạch là giao của các miền nghiệm của các bất phương trình trong hệ. Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không kể đoạn thẳng OC và CD).
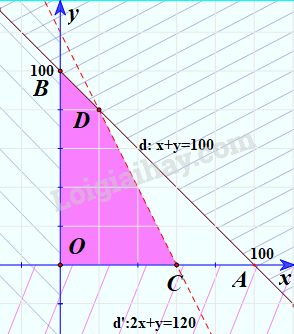
3. Ứng dụng của hệ bất phương trình bậc nhất hai ẩn
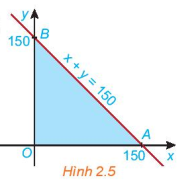
HĐ3 trang 28 Toán lớp 10: Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
Phương pháp giải:
a) Thay tọa độ điểm O, A, B vào F(x;y) và tính giá trị.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Xác định dấu:
+ So sánh x với 0
+ So sánh y với 0
Đánh giá biểu thức F(x;y) dựa vào dấu của x và y, từ đó tìm giá trị nhỏ nhất của biểu thức.
c)
Dựa vào biểu thức
Giá trị lớn nhất: Tách 2x+3y =2.(x+y)+y và dựa vào việc đánh giá x+y và y ở bước trên để tìm giá trị lớn nhất.
Lời giải:
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình nên mọi điểm (x;y) thuộc miền OAB thỏa mãn .
Vì miền OAB là miền nghiệm của hệ bất phương trình nên mọi điểm (x;y) thuộc miền OAB thỏa mãn .
Vậy và .
=>
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình nên mọi điểm (x;y) thuộc miền OAB thỏa mãn
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có .
Vậy ta có:
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.
Xem thêm lời giải Toán 10 Kết nối tri thức hay, chi tiết khác: