Với Giải toán lớp 7 trang 59 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 59 Tập 2 Cánh diều

Luyện tập 4 trang 59 Toán 7 Tập 2: Tính hiệu P(x) - Q(x) bằng hai cách, trong đó:

P(x) = 6x3 + 8x2 + 5x - 2;

Q(x) = -9x3 + 6x2 + 3 + 2x.

Lời giải:

Cách 1. Tính hiệu theo cột dọc:

Ta sắp xếp đa thức Q(x) theo số mũ giảm dần của biến x được:

Q(x) = -9x3 + 6x2 + 3 + 2x

Q(x) = -9x3 + 6x2 + 2x + 3.

Thực hiện tính hiệu P(x) – Q(x):

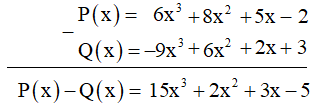
Vậy P(x) - Q(x) = 15x3 + 2x2 + 3x - 5.

Cách 2. Tính hiệu theo hàng ngang:

P(x) - Q(x)

= 6x3 + 8x2 + 5x - 2 - (-9x3 + 6x2 + 3 + 2x)

= 6x3 + 8x2 + 5x - 2 + 9x3 - 6x2 - 3 - 2x

= (6x3 + 9x3) + (8x2 - 6x2) + (5x - 2x) + (-2 - 3)

= 15x3 + 2x2 + 3x - 5.

Vậy P(x) - Q(x) = 15x3 + 2x2 + 3x - 5.

B. Bài tập

Bài 1 trang 59 Toán 7 Tập 2: Cho hai đa thức: R(x) = -8x4 + 6x3 + 2x2 - 5x + 1 và S(x) = x4 - 8x3 + 2x + 3. Tính:

a) R(x) + S(x);

b) R(x) - S(x).

Lời giải:

a) Cách 1: Tính tổng R(x) + S(x) theo cột dọc:

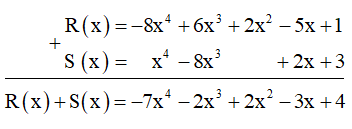
Vậy R(x) + S(x) = -7x4 - 2x3 + 2x2 - 3x + 4.

Cách 2: Tính tổng R(x) + S(x) theo hàng ngang:

R(x) + S(x)

= (-8x4 + 6x3 + 2x2 - 5x + 1) + (x4 - 8x3 + 2x + 3)

= -8x4 + 6x3 + 2x2 - 5x + 1 + x4 - 8x3 + 2x + 3

= (-8x4 + x4) + (6x3 - 8x3) + 2x2 + (-5x + 2x) + (1 + 3)

= -7x4 - 2x3 + 2x2 - 3x + 4.

Vậy R(x) + S(x) = -7x4 - 2x3 + 2x2 - 3x + 4.

b) Cách 1: Tính hiệu R(x) ‒ S(x) theo cột dọc:

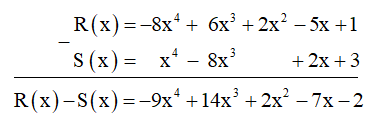
Vậy R(x) - S(x) = -9x4 + 14x3 + 2x2 - 7x - 2.

Cách 2: Tính hiệu R(x) ‒ S(x) theo hàng ngang:

R(x) - S(x) = (-8x4 + 6x3 + 2x2 - 5x + 1) - (x4 - 8x3 + 2x + 3)

= -8x4 + 6x3 + 2x2 - 5x + 1 - x4 + 8x3 - 2x - 3

= (-8x4 - x4) + (6x3 + 8x3) + 2x2 + (-5x - 2x) + (1 - 3)

= -9x4 + 14x3 + 2x2 - 7x - 2

Vậy R(x) - S(x) = -9x4 + 14x3 + 2x2 - 7x - 2.

Bài 2 trang 59 Toán 7 Tập 2: Xác định bậc của hai đa thức là tổng, hiệu của:

A(x) = -8x5 + 6x4 + 2x2 - 5x + 1 và B(x) = 8x5 + 8x3 + 2x - 3.

Lời giải:

- Ta có thể thực hiện A(x) + B(x) theo hai cách

Cách 1: Cộng theo cột dọc:

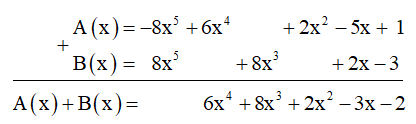
Cách 2: Cộng theo hàng ngang:

A(x) + B(x) = -8x5 + 6x4 + 2x2 - 5x + 1 + 8x5 + 8x3 + 2x - 3

= (-8x5 + 8x5) + 6x4 + 8x3 + 2x2 + (-5x + 2x) + (1 - 3)

= 6x4 + 8x3 + 2x2 - 3x - 2

Do đó A(x) + B(x) = 6x4 + 8x3 + 2x2 - 3x - 2

Vậy bậc của đa thức A(x) + B(x) là 4.

- Ta có thể thực hiện A(x) ‒ B(x) theo hai cách

Cách 1: Trừ theo cột dọc:

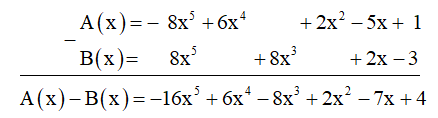
Cách 2: Trừ theo hàng ngang:

A(x) - B(x)

= -8x5 + 6x4 + 2x2 - 5x + 1 - (8x5 + 8x3 + 2x - 3)

= -8x5 + 6x4 + 2x2 - 5x + 1 - 8x5 - 8x3 - 2x + 3

= (-8x5 - 8x5) + 6x4 - 8x3 + 2x2 + (-5x - 2x) + (1 + 3)

= -16x5 + 6x4 - 8x3 + 2x2 - 7x + 4

Do đó A(x) - B(x) = -16x5 + 6x4 - 8x3 + 2x2 - 7x + 4

Vậy bậc của đa thức A(x) - B(x) là 5.

Bài 3 trang 59 Toán 7 Tập 2: Bác Ngọc gửi ngân hàng thứ nhất 90 triệu đồng với kì hạn 1 năm, lãi suất x%/năm. Bác Ngọc gửi ngân hàng thứ hai 80 triệu đồng với kì hạn 1 năm, lãi suất (x + 1,5)%/năm. Hết kì hạn 1 năm, bác Ngọc có được cả gốc và lãi là bao nhiêu:

a) Ở ngân hàng thứ hai?

b) Ở cả hai ngân hàng?

Lời giải:

a) Khi hết kì hạn 1 năm thì tiền lãi bác Ngọc nhận được ở ngân hàng thứ hai là:

80 . (x + 1,5)% = $80.\frac{x+\mathrm{1,5}}{100}$ = $\frac{4}{5}$(x + 1,5) = 0,8x + 1,2 (triệu đồng).

Khi hết kì hạn 1 năm, bác Ngọc có được cả gốc và lãi ở ngân hàng thứ hai là:

80 + 0,8x + 1,2 = 0,8x + 81,2 (triệu đồng).

Vậy bác Ngọc nhận được 0,8x + 81,2 triệu đồng cả gốc lẫn lãi ở ngân hàng thứ hai khi hết kì hạn 1 năm.

b) Khi hết kì hạn 1 năm thì tiền lãi bác Ngọc nhận được ở ngân hàng thứ nhất là:

90 . x% = 90 . $\frac{x}{100}$ = $\frac{9}{10}$x = 0,9x (triệu đồng).

Khi hết kì hạn 1 năm, bác Ngọc có được cả gốc và lãi ở ngân hàng thứ nhất là:

90 + 0,9x (triệu đồng).

Khi hết kì hạn 1 năm, bác Ngọc có được cả gốc và lãi ở cả hai ngân hàng là:

0,8x + 81,2 + 90 + 0,9x = 1,7x + 171,2 (triệu đồng).

Vậy bác Ngọc nhận được 1,7x + 171,2 triệu đồng cả gốc lẫn lãi ở cả hai ngân hàng khi hết kì hạn 1 năm.

Bài 4 trang 59 Toán 7 Tập 2: Người ta rót nước từ một can đựng 10 lít nước sang một bể rỗng có dạng hình lập phương với độ dài cạnh 20 cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1 dm3.

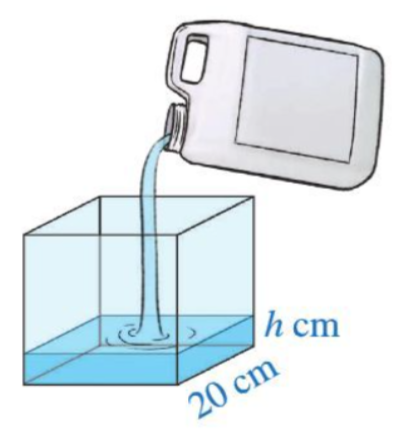
Lời giải:

Thể tích nước trong bể khi mực nước có chiều cao h (cm) là:

20 . 20 . h = 400h (cm3).

Đổi 400h cm3 = 0,4h dm3; 10 lít = 10 dm3.

Thể tích nước trong can ban đầu là 10 dm3.

Thể tích nước trong bể hình lập phương chính là thể tích nước trong can rót ra nên thể tích nước còn lại trong can là: 10 - 0,4h (dm3).

Vậy thể tích nước trong can còn lại là 10 – 0,4h dm3.

Bài 5 trang 59 Toán 7 Tập 2: Bạn Minh cho rằng “Tổng của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Bạn Quân cho rằng “Hiệu của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Hai bạn Minh và Quân nói như vậy có đúng không? Giải thích vì sao.

Lời giải:

Minh và Quân nói như vậy là không đúng vì tổng hoặc hiệu của hai đa thức bậc bốn có thể không phải là đa thức bậc bốn.

Ví dụ như: Với hai đa thức A(x) = 2x4; B(x) = -2x4 + x2; C(x) = 2x4 + x.

Ta có:

A(x) + B(x) = 2x4 + (-2x4 + x2) = 2x4 - 2x4 + x2 = (2x4 - 2x4) + x2 = x2 là đa thức bậc hai. Do đó Minh nói sai.

A(x) - C(x) = 2x4 - (2x4 + x) = 2x4 - 2x4 ‒ x = (2x4 - 2x4) ‒ x = ‒x là đa thức bậc một. Do đó Quân nói sai.

Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Giải Toán 7 trang 54 Tập 2

Giải Toán 7 trang 55 Tập 2

Giải Toán 7 trang 56 Tập 2

Giải Toán 7 trang 57 Tập 2

Giải Toán 7 trang 58 Tập 2