Với Giải toán lớp 7 trang 58 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 58 Tập 2 Cánh diều

Luyện tập 3 trang 58 Toán 7 Tập 2: Cho hai đa thức: $P\left(x\right)=2x^2-5x-\frac{1}{3}$ và $Q\left(x\right)=-6x^4+5x^2+\frac{2}{3} + 3x.$  

Tính hiệu P(x) - Q(x).

Lời giải:

Sắp xếp đa thức Q(x) theo số mũ giảm dần của biến x như sau:

$Q\left(x\right)=-6x^4+5x^2+\frac{2}{3} + 3x$

$Q\left(x\right)=-6x^4+5x^2+\frac{2}{3} + 3x.$

Ta có:

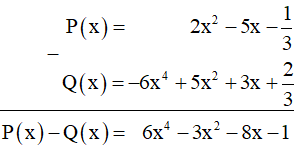
Vậy P(x) - Q(x) = 6x4 - 3x2 - 8x - 1.

Hoạt động 6 trang 58 Toán 7 Tập 2: Cho hai đa thức: P(x) = -3x2 + 2 + 7x và Q(x) = -4x + 5x2 + 1.

a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến.

b) Viết hiệu P(x) - Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc.

c) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau.

d) Tính hiệu của P(x) - Q(x) bằng cách thực hiện phép tính trong từng nhóm.

Lời giải:

a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến ta có:

P(x) = -3x2 + 2 + 7x = -3x2 + 7x + 2.

Q(x) = -4x + 5x2 + 1 = 5x2 + (-4x) + 1 = 5x2 - 4x + 1.

b) Viết hiệu P(x) - Q(x) theo hàng ngang trong đó đa thức Q(x) được đặt trong dấu ngoặc:

P(x) - Q(x)

= -3x2 + 7x + 2 - (5x2 - 4x + 1)

c) Bỏ dấu ngoặc và nhóm các đơn thức có cùng số mũ của biến với nhau ta có:

P(x) - Q(x)

= -3x2 + 7x + 2 - (5x2 - 4x + 1)

= -3x2 + 7x + 2 - 5x2 + 4x - 1

= (-3x2 - 5x2) + (7x + 4x) + (2 - 1)

d) Tính hiệu:

P(x) - Q(x)

= (-3x2 - 5x2) + (7x + 4x) + (2 - 1)

= -8x2 + 11x + 1.

Vậy P(x) - Q(x) = -8x2 + 11x + 1.

Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Giải Toán 7 trang 54 Tập 2

Giải Toán 7 trang 55 Tập 2

Giải Toán 7 trang 56 Tập 2

Giải Toán 7 trang 57 Tập 2

Giải Toán 7 trang 59 Tập 2