Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Ôn tập chương 2: Đường tròn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Ôn tập chương 2: Đường tròn
Tứ giác là hình gì Vì sao
Chứng minh hệ thức
Chứng minh rằng là tiếp tuyến chung của các nửa đường tròn có đường kính và
Điểm ở vị trí nào trên thì có độ dài lớn nhất
Phương pháp giải:
Sử dụng kiến thức:
+) Tứ giác có ba góc vuông là hình chữ nhật.
+) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
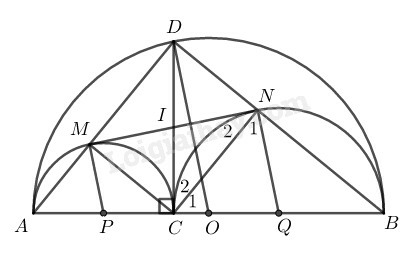
Tam giác nội tiếp trong đường tròn có là đường kính nên hay
Tam giác nội tiếp đường tròn có là đường kính nên
Suy ra:
Tam giác nội tiếp trong đường tròn có là đường kính nên
Suy ra:
Tứ giác có ba góc vuông nên nó là hình chữ nhật.
Tam giác vuông tại có
Theo hệ thức lượng trong tam giác vuông, ta có:
Tam giác vuông tại có
Theo hệ thức lượng trong tam giác vuông, ta có:
Từ và suy ra:
Gọi là trung điểm của là trung điểm của là giao điểm của với
Vì là hình chữ nhật nên
Tam giác cân tại nên
Tam giác cân tại nên
Vì nên
Từ và suy ra: hay
Vậy là tiếp tuyến của đường tròn đường kính
Tam giác cân tại nên
Tam giác cân tại nên
Vì nên
Từ và suy ra: hay
Vậy là tiếp tuyến của đường tròn đường kính
Gọi là trung điểm của
Tứ giác là hình chữ nhật nên
Trong tam giác ta có: nên
Vì không đổi nên là giá trị lớn nhất khi và chỉ khi trùng với
Vậy là trung điểm của thì có độ dài lớn nhất.
Tứ giác là hình gì Vì sao
Chứng minh hệ thức
Chứng minh rằng là tiếp tuyến của đường tròn có đường kính là
Tính độ dài biết rằng
Phương pháp giải:
Sử dụng kiến thức:
) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
) Tứ giác có ba góc vuông là hình chữ nhật.
) Hệ thức lượng trong tam giác vuông:
+) Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu hai cạnh góc vuông trên cạnh huyền.
Lời giải:
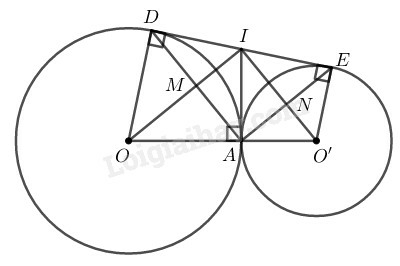
Trong đường tròn ta có là tia phân giác của góc ( tính chất hai tiếp tuyến cắt nhau IA và ID)
Trong đường tròn ta có là tia phân giác của góc (tính chất hai tiếp tuyến cắt nhau IA và IE)
Mà góc và góc là hai góc kề bù nên ( tính chất hai góc kề bù)
hay
Xét đường tròn (O) có ((tính chất hai tiếp tuyến cắt nhau IA và ID)
Tam giác cân tại
Tam giác cân tại I có là phân giác của góc nên cũng là đường cao của tam giác
hay
Xét đường tròn (O') có (tính chất hai tiếp tuyến cắt nhau IA và IE)
Tam giác cân tại
Tam giác cân có là phân giác của góc nên cũng là đường cao của tam giác
hay
Tứ giác là hình chữ nhật ( Tứ giác có ba góc vuông)
Tam giác vuông tại có
Theo hệ thức lượng trong tam giác vuông , ta có:
Tam giác vuông tại có
Theo hệ thức lượng trong tam giác vuông , ta có:
Từ và suy ra:
Ta có: và ( chứng minh trên) nên
nằm trên đường tròn tâm đường kính
Vì tại nên là tiếp tuyến của đường tròn
Tam giác vuông tại có
Theo hệ thức lượng trong tam giác vuông , ta có:
Mà nên
Sử dụng kiến thức:
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có ba góc vuông là hình chữ nhật.
Lời giải:
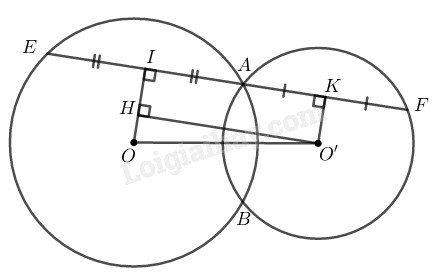
Kẻ
Trong đường tròn có mà OI là 1 phần đường kính và AE là dây cung nên:
( đường kính vuông góc với dây cung)
Trong đường tròn có mà O'K là 1 phần đường kính và AF là dây cung nên:
(đường kính vuông góc với dây cung)
Ta có:
Suy ra:
Kẻ
Khi đó tứ giác là hình chữ nhật ( có ba góc vuông)
Suy ra:
Trong tam giác ta có:
Suy ra:
Từ và suy ra:
Ta có: khi và trùng nhau hay
Vậy có độ dài lớn nhất bằng khi và chỉ khi
Tam giác là tam giác cân ;
Tam giác là tam giác cân ;
là tiếp tuyến của đường tròn
Phương pháp giải:
Sử dụng kiến thức:
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Trong tam giác cân, đường cao ứng với cạnh đáy cũng là đường phân giác, trung tuyến, trung trực.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
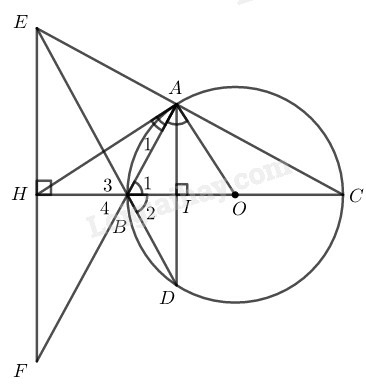
Gọi là giao điểm của và .
Xét đường tròn (O) có đường kính tại I nên I là trung điểm của dây AD (định lý)
Suy ra là đường trung trực của nên theo tính chất đường trung trực ta có:
Tam giác cân tại có nên là tia phân giác của góc
Suy ra:
Mà (đối đỉnh)
và ( đối đỉnh)
Suy ra:
Do đó là tia phân giác của góc
Tam giác có là tia phân giác của góc và nên tam giác cân tại
Tam giác cân tại có BH là đường cao nên BH cũng là đường trung tuyến.
Suy ra
Tam giác vuông tại có là đường trung tuyến ứng với cạnh huyền nên:
(tính chất tam giác vuông)
Vậy tam giác cân tại
Tam giác cân tại nên
Tam giác cân tại nên
Mà ( đối đỉnh)
Suy ra:
Từ và suy ra:
Tam giác vuông tại nên
Từ và suy ra: hay
Vậy là tiếp tuyến của đường tròn
Chứng minh rằng
Gọi là điểm đối xứng với qua Chứng minh rằng là tiếp tuyến của đường tròn
Chứng minh rằng là tiếp tuyến của đường tròn
Phương pháp giải:
Sử dụng kiến thức:
+) Tam giác nội tiếp đường tròn, có một cạnh là đường kính thì tam giác đó là tam giác vuông.
+) Trong tam giác, ba đường cao cắt nhau tại một điểm gọi là trực tâm tam giác.
+) Hai điểm gọi là đối xứng với nhau qua nếu là trung điểm của đoạn thẳng nối hai điểm đó.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
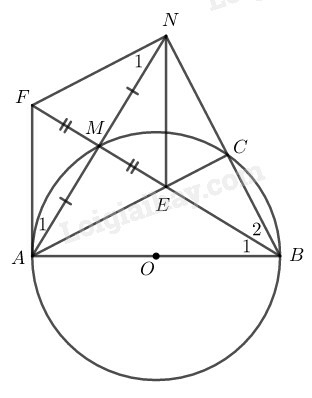
Tam giác nội tiếp trong đường tròn có là đường kính nên vuông tại
Suy ra:
Tam giác nội tiếp trong đường tròn có là đường kính nên vuông tại
Suy ra:
Tam giác có hai đường cao và cắt nhau tại nên là trực tâm của tam giác
Suy ra:
Ta có: ( tính chất đối xứng tâm)
( tính chất đối xứng tâm)
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi điểm đường nên nó là hình bình hành.
Suy ra:
Mà ( chứng minh trên)
Suy ra: tại
Vậy là tiếp tuyến của đường tròn
Trong tam giác ta có: và hay BM vừa là đường cao vừa là đường trung tuyến nên tam giác cân tại
Suy ra hay thuộc đường tròn
Tứ giác là hình bình hành nên hay
Mặt khác: ( chứng minh trên)
Suy ra: tại
Vậy là tiếp tuyến của đường tròn
Hai đường tròn và có vị trí tương đối như thế nào đối với nhau
Kẻ dây của đường tròn vuông góc với tại trung điểm của Tứ giác là hình gì Vì sao
Gọi là giao điểm của và đường tròn Chứng minh rằng ba điểm thẳng hàng.
Chứng minh rằng là tiếp tuyến của đường tròn
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu thì đường tròn và đường tròn tiếp xúc trong.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
+) Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm xác định được hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thìđường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
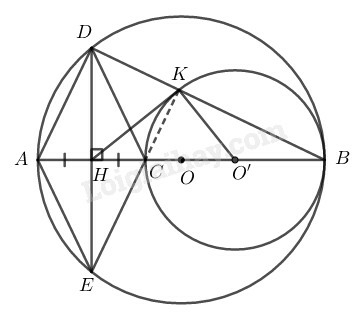
Vì và thẳng hàng nên: nằm giữa và
Ta có:
Vậy đường tròn tiếp xúc trong với đường tròn tại
Xét đường tròn (O) có mà AB là đường kính, DE là dây cung
Suy ra: (đường kính vuông góc với dây cung)
Lại có:
Suy ra, tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có:
Suy ra tứ giác là hình thoi.
Tam giác nội tiếp trong đường tròn có là đường kính nên vuông tại
Suy ra:
Tứ giác là hình thoi nên
Suy ra:
Tam giác nội tiếp trong đường tròn có là đường kính nên vuông tại
Suy ra:
Từ và suy ra trùng với
Vậy thẳng hàng.
Tam giác vuông tại có là trung tuyến ứng với cạnh huyền nên:
(tính chất tam giác vuông)
Suy ra tam giác cân tại
Suy ra: (tính chất tam giác cân)
Ta có: (= bán kính đường tròn (O')) nên tam giác cân tại
Suy ra: (tính chất tam giác cân)
Mà: (đối đỉnh)
Suy ra:
Từ và suy ra:
Tam giác vuông tại nên
Từ và suy ra: hay tại
Vậy là tiếp tuyến của đường tròn
Chứng minh rằng tứ giác là hình thoi.
Gọi là giao điểm của và đường tròn Chứng minh rằng ba điểm thẳng hàng.
Chứng minh rằng là tiếp tuyến của đường tròn
Phương pháp giải:
Sử dụng kiến thức:
+) Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
+) Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm xác định được hai đường thẳng cùng vuông góc với một đường thẳng thứ ba.
+) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
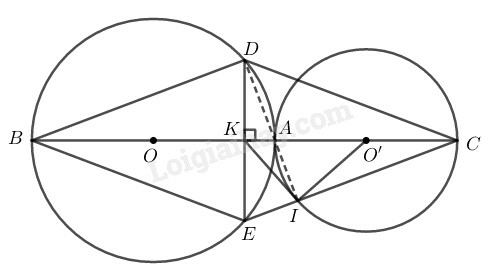
Vì đường tròn và tiếp xúc ngoài tại nên và thẳng hàng.
Trong đường tròn ta có: tại mà AB là đường kính và DE là dây cung
Suy ra: ( đường kính vuông góc với dây cung)
Lại có:
Suy ra tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có:
Suy ra tứ giác là hình thoi.
Tam giác nội tiếp trong đường tròn có là đường kính nên vuông tại
Suy ra:
Tứ giác là hình thoi nên
Suy ra:
Tam giác nội tiếp trong đường tròn có là đường kính nên vuông tại
Suy ra:
Từ và suy ra trùng với
Vậy thẳng hàng.
c) Tam giác vuông tại có là trung tuyến ứng với cạnh huyền nên:
( tính chất tam giác vuông)
Suy ra tam giác cân tại
Suy ra: hay
Ta có: (= bán kính đường tròn (O')) nên tam giác cân tại
Suy ra: ( tính chất tam giác cân)
Mà: (đối đỉnh)
Suy ra:
Từ và suy ra:
Xét tam giác KAD vuông tại K có:
Suy ra hay tại
Vậy là tiếp tuyến của đường tròn
Chứng minh rằng ba điểm thẳng hàng và là tiếp tuyến của đường tròn
Chứng minh rằng khi điểm di chuyển trên nửa đường tròn thì tổng không đổi.
Giả sử và cắt nhau tại Chứng minh rằng tích không đổi.
Phương pháp giải:
Sử dụng kiến thức:
) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hìnhchiếu cạnh góc vuông đó trên cạnh huyền.
Lời giải:
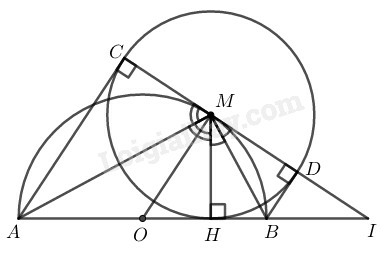
Trong đường tròn có AC và AH là 2 tiếp tuyến cắt nhau tại A, theo tính chất hai tiếp tuyến cắt nhau, ta có: là tia phân giác của góc và
Suy ra: hay
Trong đường tròn có BD và BH là 2 tiếp tuyến cắt nhau tại B, theo tính chất hai tiếp tuyến cắt nhau, ta có: là tia phân giác của góc và
Suy ra: hay
Tam giác nội tiếp đường tròn có là đường kính nên vuông tại
Suy ra: hay
Suy ra:
Vậy thẳng hàng.
Theo câu a) ta có: và
Khi thay đổi trên nửa đường tròn tâm thì luôn bằng và luôn bằng
Suy ra: không đổi
Ta có: và ( tính chất tiếp tuyến)
Suy ra: hay tứ giác là hình thang
Mà (= bán kính )
Và (= bán kính )
Suy ra là đường trung bình của hình thang
Khi đó Suy ra: hay
Tam giác vuông tại có
Theo hệ thức lượng trong tam giác vuông, ta có:
Mà OM là bán kính đường tròn (O) nên OM có độ dài không đổi.
Suy ra: không đổi.
Bài tập bổ sung (trang 173 SBT Toán 9)
Hãy chọn phương án đúng.
Phương pháp giải:
Sử dụng kiến thức:
+) Trong tam giác đều, giao ba đường trung tuyến cũng là giao ba đường phân giác, ba đường cao, đường trung trực (tâm đường tròn nội tiếp cũng là tâm đường tròn ngoại tiếp).
+) Trọng tâm tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến ứng với đỉnh đó.
Lời giải:
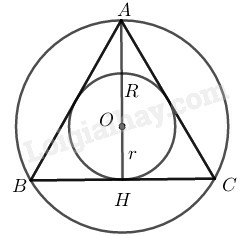
Giả sử đều ngoại tiếp đường tròn , nội tiếp đường
Gọi là trung điểm của
Vì O là trọng tâm tam giác ABC (vì tam giác ABC đều)
Chọn
là tiếp tuyến của nửa đường tròn.
Phương pháp giải:
Chứng minh hai tam giác đồng dạng để thiết lập tỉ số giữa các cạnh, từ đó chứng minh được biểu thức đề bài đưa ra.
Theo tính chất của tiếp tuyến, ta phải chứng minh được tại
Áp dụng: Trong tam giác vuông đường trung tuyến ứng với canh huyền thì bằng nửa cạnh huyền.
Từ đó ta tìm các góc bằng nhau, thiết lập mối liên hệ giữa chúng.
Lời giải:
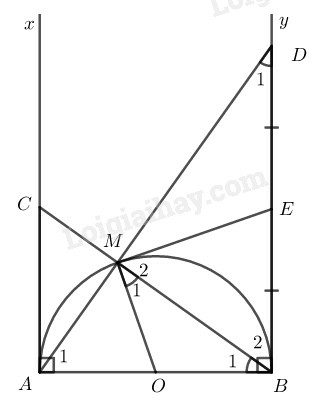
Xét tam giác ABD vuông tại B có (1)
Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính nên vuông tại M.
Suy ra (2)
Từ (1) và (2) suy ra: ( cùng phụ với ).
Xét và có:
(cmt)
Suy ra đồng dạng với suy ra:
(cặp cạnh tương ứng tỉ lệ), do đó
Vì tam giác AMB vuông tại M (cmt) nên
Suy ra tam giác BMD vuông tại M.
Ta có vuông tại M có ME là đường trung tuyến nên
Suy ra cân tại E nên
Lại có cân tại (do nên
Từ và suy ra
=
Hay tức là tại
Vậy là tiếp tuyến của nửa đường tròn (O).