Với giải Bài 7 trang 87 Toán lớp 7 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 4

Bài 7 trang 87 Toán lớp 7: Cho Hình 6, biết hai đường thẳng a và b song song với nhau và $\widehat{A_1}={50}^{\circ }$

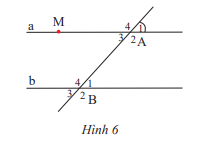
a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.

b) Tính số đo của $\widehat{A_3},\widehat{B_3}$

c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c $\mathrm{\perp }$ b.

Lời giải:

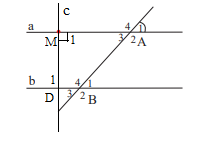
a) Các cặp góc so le trong là: $\widehat{A_3}=\widehat{B_1};\widehat{A_2}=\widehat{B_4}$

Các cặp góc đồng vị là : $\widehat{A_1}=\widehat{B_1};\widehat{A_2}=\widehat{B_2};\widehat{A_3}=\widehat{B_3};\widehat{A_4}=\widehat{B_4}$

b) Vì $\widehat{A_1}=\widehat{A_3}$ (2 góc đối đỉnh), mà $\widehat{A_1}={50}^{\circ }$ nên $\widehat{A_3}={50}^{\circ }$

Vì a // b nên $\widehat{A_3}=\widehat{B_3}$( 2 góc đồng vị), mà $\widehat{A_3}={50}^{\circ }$ nên $\widehat{B_3}={50}^{\circ }$

c) Gọi c cắt b tại D

Vì a // b nên $\widehat{M_1}=\widehat{D_1}$ ( 2 góc so le trong), mà $\widehat{M_1}={90}^{\circ }\Rightarrow \widehat{D_1}={90}^{\circ }$

Vậy c $\mathrm{\perp }$ b.

Chú ý: Ta có định lí: Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng song song vói đường thẳng còn lại

Bài tập vận dụng:

Bài 1:

a) Hãy kể tên các cặp góc kề nhau trong hình vẽ.

b) Tìm số đo của góc $\widehat{xOz}$, biết $\widehat{xOy}={70}^0$ và $\widehat{yOz}={55}^0$.

Hướng dẫn giải

a) Các cặp góc kề nhau:

$\widehat{xOy}$ và $\widehat{yOz}$ (vì có cạnh chung Oy và không có điểm trong chung).

$\widehat{xOy}$ và $\widehat{tOy}$ (vì có cạnh chung Oy và không có điểm trong chung).

$\widehat{xOz}$ và $\widehat{tOz}$ (vì có cạnh chung Oz và không có điểm trong chung).

$\widehat{yOz}$ và $\widehat{tOz}$ (vì có cạnh chung Oz và không có điểm trong chung).

b) Vì $\widehat{xOy}$ và $\widehat{yOz}$ là hai góc kề nhau nên :

$\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

Suy ra: $\widehat{xOz}={70}^0+{55}^0={125}^0$

Vậy $\widehat{xOz}={125}^0$.

Bài 2: Cho hai góc $\widehat{xOy}$ và $\widehat{yOz}$ kề bù với nhau. Biết $\widehat{xOy}={30}^0$. Tính $\widehat{yOz}$.

Hướng dẫn giải

Vì hai góc $\widehat{xOy}$ và $\widehat{yOz}$ kề bù với nhau nên $\widehat{xOy}+\widehat{yOz}={180}^0$ .

Suy ra: $\widehat{yOz}={180}^0-\widehat{xOy}$.

Do đó $\widehat{yOz}={180}^0-{30}^0={150}^0$.

Vậy $\widehat{yOz}={150}^0$.

Bài 3: Tính các góc $\widehat{A_2};\widehat{A_3};\widehat{A_4}$ trong hình, biết $\widehat{A_1}={40}^0$.

Hướng dẫn giải

Ta có $\widehat{A_3}=\widehat{A_1}={40}^0$ (hai góc đối đỉnh).

Ta có $\widehat{A_1}+\widehat{A_2}={180}^0$ (hai góc kề bù)

Suy ra $\widehat{A_2}={180}^0-\widehat{A_1}={180}^0-{40}^0={140}^0$.

$\widehat{A_4}=\widehat{A_2}={140}^0$ (hai góc đối đỉnh)

Vậy $\widehat{A_2}{\text{= 140}}^0;\widehat{A_3}={40}^0;\widehat{A_4}={140}^0$.

Xem thêm các bài giải Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1 trang 86 Toán lớp 7: Trong những câu sau, em hãy chọn những câu đúng...

Bài 2 trang 86 Toán lớp 7: Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1...

Bài 3 trang 87 Toán lớp 7: Quan sát Hình 2. Chứng minh rằng xy // zt...

Bài 4 trang 87 Toán lớp 7: Quan sát Hình 3...

Bài 5 trang 87 Toán lớp 7: Quan sát Hình 4. Chứng minh rằng:...

Bài 6 trang 87 Toán lớp 7: Cho Hình 5 có $\widehat{B_1}=130°$. Số đo của $\widehat{A_1}$ là bao nhiêu?...

Bài 8 trang 87 Toán lớp 7: Vẽ đường thẳng m song song với đường thẳng n. Vẽ đường thẳng d cắt đường thẳng m tại điểm I...

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Bài 5: Hoạt động thực hành và trải nghiệm: Vẽ hai đường song song và đo góc bằng phần mềm GeoGebra

Bài tập cuối chương 4

Bài 1: Thu thập và phân loại dữ liệu

Bài 2: Biểu đồ hình quạt tròn

Bài 3: Biểu đồ đoạn thẳng